はじめに
酵素の活性部位は通常アミノ酸残基からなり、どのアミノ酸残基が存在するかによって基質の特異性が大きく変化することが知られています。 酵素はpHによって、その物性(主に電荷)が変化する。 電荷が変化すると、活性部位のアミノ酸残基と流入する基質との相互作用が変化することがある。 このため、基質は水素結合やファンデルワールス力によって活性部位に結合することができる。 基質が活性部位に結合すると、酵素-基質複合体が形成され、さらなる化学反応に関与する。
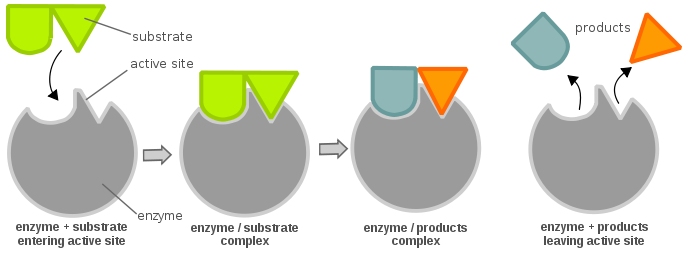
酵素が活性化し、化学反応を進行させるためにエネルギー的に有利になるためには、基質が酵素の「活性部位」に結合することが必要である。 活性部位は錠前、基質は鍵として考えることができ、これは錠前と鍵のモデルとして知られている。 鍵(基質)を差し込んで回すと(化学反応)、鍵(酵素)が開き(生成物生成)、生成物ができる。 なお、酵素は複数の活性部位を持つことがある。 活性部位と基質の関係については、もう一つの説として「誘導適合説」があり、これは「鍵と錠」説(活性部位は一見柔軟性がないように見える)とは全く逆のものである。 酵素の活性部位は非常に柔軟で、基質が結合したときだけそのコンフォメーションを変えるという説である
酵素は、酵素-基質複合体の活性化のギブス自由エネルギーを下げることによって触媒として働く。 以下は、触媒がある場合とない場合の基本的な酵素反応を示す2つの図である:
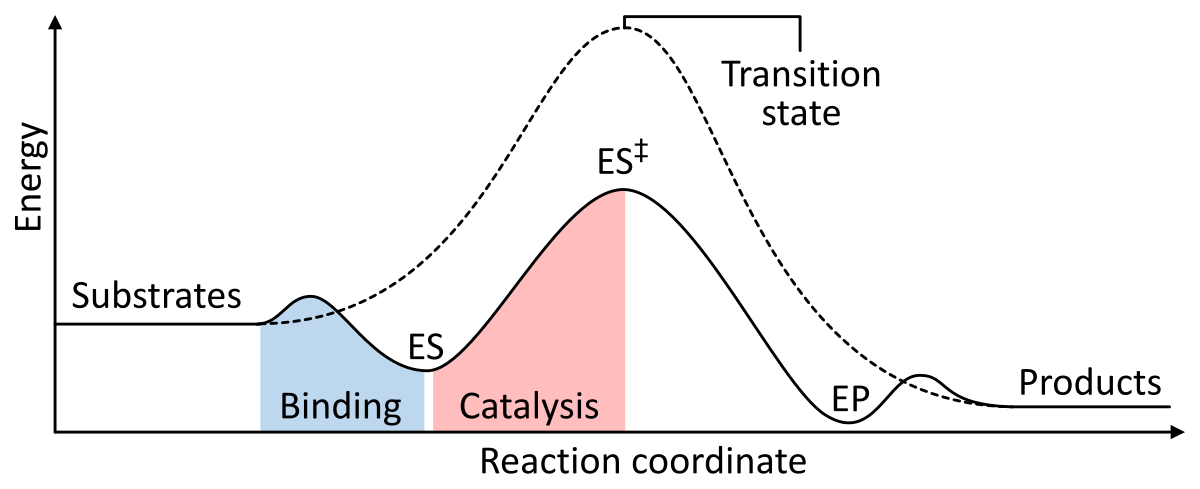
図1:化学反応の各段階のエネルギーを示す。 無触媒の場合(破線)、基質は遷移状態に到達するために多くの活性化エネルギーを必要とし、その後、よりエネルギーの低い生成物に分解される。 酵素触媒反応(実線)では、酵素が基質(ES)と結合し、遷移状態(ES‡)を安定化させて生成物(EP)を生成するのに必要な活性化エネルギーを減らし、最終的に放出する。 Wikipediaより
酵素の効率は次のように決定できます。単純な酵素反応を考えてみましょう。
ドイツの生化学者レオノール・ミカエリスとカナダの生化学者モード・メンテンが、この系を記述する方程式を導き、後に「ミカエリス・メンテン方程式」として知られる、以下のようになりました。 \tag{1}}
この式は、反応が進行する最大速度であるVmaxとミカエリス定数KMが既知であるとして、ある基質濃度での反応速度を与えるものである。 しかし、実際のミカエリス・メンテンでは、V0を測定し、Vmaxをデータプロット上の飽和あるいはプラトーとして観察することが多い。 基質濃度は既知なので、通常はKMが計算値として注目されます。
ここで、 \(V_0= \dfrac{V_max}{2}):
³{K_M + } とします。 \tag{2}]
Comments) \V_{max}}{2} = V_{max} とする。 \tag{3}}{V_{max}}{diffrac{V_{max}}{2}} = \dfrac{V_{max}}{diffrac{V_{max}}}{2}} \♪♪~ \tag{5}} = 2 \tag{6}}
ミカエリス定数は、基質と酵素の複合体が生成物になる場合と、基質が酵素に結合しなくなる場合とがあり、基質が酵素から結合しなくなる速度と考えることができる。 KMは式で示すことができる。
ここで、k-1は基質が酵素に結合しなくなり、酵素-基質複合体が解離する速度定数、k2は基質-酵素複合体が消失して生成物となる速度定数、K1は基質-酵素複合体が生成するときの速度定数である。 したがって、KM は基質-酵素複合体消失速度を基質-酵素複合体形成速度で割ったものと見ることができ、基質の半分が酵素に結合しているレベルであることがわかる。 KM の変化を調べ、対照系(阻害剤の存在しないことが分かっている生物系)と比較することができるため、KM は阻害剤の存在を示す有用な指標となる。 KM は従属変数であり、その値は、系の pH レベル、温度、または化学反応に影響を与える可能性のあるその他の条件など、多くの理由により変化する可能性があります。 KMが小さいということは、基質が酵素に対して高い親和性を持っていることを示す。
ミカエリス-メンテン式は、次のようにv0を 、に対してプロットすると、酵素効率を測定するのに最も有用である。 from Wikipedia.
Vmax とは、「基質を増やしても、それ以上速く反応できない」という意味で、, に関係なく反応が進む最大速度である。 これは、Vmaxでは酵素の活性部位がすべて占有されているためです。 以上、様々な形式の酵素動力学式について説明した後、触媒効率の結論に至った。 図3を参照すると、次のようになります:
³{dfrac{k_{-1} + k_2}{k_1} + ここで、k2はkcat(酵素の触媒効率)とも呼ばれる。 前の議論から、v0は測定された反応速度で、時間の経過とともに生成物が形成されるので、式は次のようになると結論付けることができます:
{dt} = k_2_0 \tag{9}]
ここで0は全酵素濃度です。
また、VMaxは酵素-基質複合体がすべて消失して生成物になるときに観測されることが知られているので、以下の仮定を立てることができる:
0 \tag{10} \Ίταμμα για για για για για για για για για για για γιβή} \実験データを得て、Michaelis-Menten式を用いた後に使用する触媒効率の計算式である。 kcatが大きければ、酵素の量が少なくてすむので効率的である
。