これらは再帰構造を持つ確率的学習過程で、ANNで用いられる初期の最適化技術の基礎になっている。 ボルツマンマシンは、1985年にGeoffrey HintonとTerry Sejnowskiによって発明された。 このネットワークの驚くべき特徴は、局所的に利用可能な情報のみを使用することである。 2040>
ボルツマンマシンに関するいくつかの重要なポイント –
-
再帰構造を用いる。
-
確率的ニューロンからなり、1か0の2通りの状態のうちどちらかを持つ。
-
この中のいくつかのニューロンは適応的(自由状態)で、いくつかはクランプ(凍結状態)である。
-
離散ホップフィールドネットワークにシミュレーションアニーリングを適用すると、ボルツマンマシンとなる。
ボルツマンマシンの目的
ボルツマンマシンの主な目的は、問題の解を最適化することである。 その問題に関連する重さと量を最適化するのがボルツマンマシンの仕事である。
アーキテクチャ
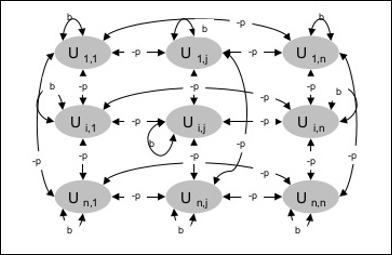
下図はボルツマンマシンのアーキテクチャを示す。 図から明らかなように、ユニットが2次元に配列されている。 ここで、ユニット間の相互接続の重みは-p(p<2853>0)、自己接続の重みはb(b<2853>0)で与えられる。
Training Algorithm
Boltzmann machineが固定した重みを持つことがわかっているので、ネットワークの重みを更新する必要はないため学習アルゴリズムはないだろう。 しかし、ネットワークをテストするためには、重みを設定し、コンセンサス関数(CF)を求める必要がある。
ボルツマンマシンはユニットUiとUjのセットを持ち、それらの上に双方向の接続を持っている。
-
ここでは固定重みをwijとする。
-
wij ≠ 0 UiとUjが連結されていれば0である。
-
また重み付き相互接続には対称性が存在する。すなわち、wij=wji.
-
wiiも存在し、すなわちユニット間の自己接続が存在するであろう。
-
任意のユニットUiについて、その状態uiは1または0のいずれかであろう。
ボルツマンマシンの主目的はコンセンサス関数(CF)の最大化であり、それは次の関係で与えられる
$$CF:= \:Limits_{i} \displaystylesumlimits_j} w_{ij}u_{i}u_{j}$
さて、状態が1から0、0から1に変化するとき、コンセンサスの変化は以下の関係で与えることができる –
$$Tenta CF:==(1}:(-}: 2u_{i})(w_{ij}: +}: \displaystylesumцlimits_{j}neq i} u_{i} w_{ij})$$
ここでuiは現在のUiの状態である。
係数の変化(1 – 2ui)は以下の関係で与えられる –
$(1}:-2u_{i})\:={begin{cases}+1, & U_{i} :is :current}.Ui (1:-2:2u_{i}){cases}は、(1:-1:2)の関係で与えられる (1:-1:2:2)である。off\-1, & U_{i}}:is:current:on ↘end{cases}$$
一般にユニットUiは状態を変更しないが、もし変更した場合はその情報はユニットにローカルに存 在することになる。
ネットワークがユニットの状態変化を受け入れる確率は、以下の関係式で与えられる。 CFが最大値になると減少する。
テストアルゴリズム
ステップ1 -初期化して学習を開始する-
- 問題の制約を表す重み
- 制御パラメータT
ステップ2 -停止条件が成立しない場合はステップ3〜8を続ける。
ステップ3-ステップ4〜7を行う。
ステップ4-いずれかの状態が重みを変更したと仮定し、1〜nのランダムな値として整数I,Jを選択する。
ステップ5 -コンセンサスの変化を以下のように計算する –
$$Delta CF := (1}:-[2u_{i})(w_{ij}):+[2u_{i}):\displaystyle ◇sum__limits_{j} w_{ij})$$
Step 6 – このネットワークが状態の変化を受け入れる確率を計算する
$AF(i,T)◇sum__limits_{j} u_{i} w_{ij} (u_{i}) {$$displaystyle ◇sum___{j} i_{j} {3161>$displaystyle ◇Sum___{neks} u_{neks= \frac{1}{1:+}}$
ステップ7 -以下のようにこの変化を受け入れるか拒否するかを決める –
ケースI – R < AFなら、この変化を受け入れる。
ケース II – R ≥ AF の場合、この変更を拒否します。
ここで、Rは0~1の乱数である。
ステップ8 -制御パラメータ(温度)を以下のように下げる –
T(new) = 0.95T(old)
ステップ9 -停止条件のテストは以下のようになる –
- 温度が指定値に達する
- 指定回数繰り返しても状態に変化がない