Underdetermined linear system
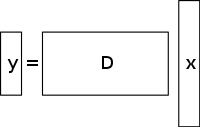
A underdetermined system of linear equationsは、方程式よりも未知数が多く、一般に解が無数に存在する系である。 下図はそのような連立方程式y = D x {displaystyle \mathbf {y} =Dmathbf {x}} を示している。 }

ここで x {displaystyle \mathbf {x} についての解を求めたい。 }

.
このような系の解を選ぶためには、適宜、余分な制約や条件(平滑性など)を課さなければならない。 圧縮センシングでは、非ゼロ係数の数が少ない解のみを許容するスパース性という制約を加える。 すべての劣決定連立方程式がスパース解を持つとは限らない。 しかし、もし劣決定系に一意な疎な解があれば、圧縮センシングの枠組みでその解を復元することができる。
解法/再構成法

圧縮センシングは、多くの興味深い信号の冗長性(それらは純粋なノイズではない)を利用する。 特に、多くの信号はスパースであり、ある領域で表現すると、ゼロに近いか等しい係数を多く含んでいます。
圧縮センシングは通常、信号が疎であることが知られている基底とは異なる基底で、圧縮測定とも呼ばれるサンプルの重み付き線形結合を取ることから始まります。 Emmanuel Candès, Justin Romberg, Terence Tao and David Donohoによって見出された結果は、これらの圧縮測定の数が少なくても、ほぼすべての有用な情報を含むことができることを示しています。 したがって、画像を意図したドメインに戻す作業は、撮影した圧縮測定の数がフル画像の画素数よりも少ないため、劣決定の行列方程式を解くことになります。 しかし、初期信号がスパースであるという制約を加えることにより、この未確定の連立方程式を解くことができる。
このような問題に対する最小二乗法は、L 2 {displaystyle L^{2}}を最小化することである。

ノルム、つまりシステムのエネルギー量を最小にすることです。 これは通常、数学的に簡単です(サンプリングされた基底の擬似逆行列による行列の乗算を含むだけです)。 しかし、これは、未知の係数が非ゼロのエネルギーを持つ多くの実用的なアプリケーションのために悪い結果をもたらす。
劣決定の連立方程式を解くときにスパース性制約を強制するには、解の非ゼロ成分の数を最小にすればよい。 ベクトルの非ゼロ成分の数を数える関数はL 0 {displaystyle L^{0}} と呼ばれた。

“norm” by David Donoho.
Candèsらは、多くの問題でL 1 {displaystyle L^{1}} が確率的であることを証明した。

ノルムはL 0 {displaystyle L^{0}} と等価であるとする。

ノルムの技術的な意味での。 この同値の結果、L 1 {displaystyle L^{1}} を解くことができる。

問題の方が L 0 {displaystyle L^{0}} より簡単である。

problem. L 1 {displaystyle L^{1}} が最も小さい候補を見つける。

ノルムは線形計画として比較的容易に表現でき、すでに効率的な解法が存在している。 測定値が有限のノイズを含む可能性がある場合、ノイズに直面してもスパース性を保持し、厳密な線形計画よりも速く解くことができるため、基底追求ノイズ除去が線形計画よりも好まれる。
全変動に基づくCS再構成
動機と応用
TV正則化の役割
全体変動は、実数値関数の空間(1変数の関数の場合)または可積分関数の空間(複数変数の関数の場合)上で定義される非負実数値関数として見ることができます。 特に信号の場合、全変動とは信号の絶対勾配の積分を指す。 信号や画像の再構成では、全変動の正則化として適用され、その基本原理は、過剰な詳細を持つ信号は全変動が大きく、エッジなどの重要な情報を保持しながらこれらの詳細を削除すると、信号の全変動が減少し、問題の元の信号に信号対象が近くなることである
信号や画像の再構成の目的のために、l 1 {displaystyle l1} {displaystyle l1} {displaystyle l1} は、信号や画像の再構成のために、全変動正則化として適用される。

最小化モデルが使用される。 また、他のアプローチとして、この記事で以前取り上げたような最小二乗法もある。 これらの方法は非常に遅く、信号のあまり完璧でない再構成を返します。 現在のCS正則化モデルは、原画像のスパース性事前分布を取り入れることでこの問題に対処しようとするもので、その1つが全変動(TV)である。 従来のTVアプローチは、断片的な定数解を与えるように設計されています。 これらのいくつかは、(先に述べたように) – 反復スキームを使用する制約付きl1-最小化。 この方法は高速ですが、その後、エッジの過度のスムージングを引き起こし、画像のエッジがぼやけることになります。 また、画像中の大きな勾配値の影響を軽減するために、繰り返し再重み付けを行うTV法が実装されています。 これは、コンピュータ断層撮影(CT)再構成において、エッジ保存型全変動として知られる方法として利用されています。 しかし、勾配値の大きさはデータ忠実度と正則化項間の相対的なペナルティ重みの推定に用いられるため、この方法はノイズやアーチファクトに対して頑健ではなく、CS画像/信号再構成に対して十分な精度を有しておらず、したがって、より小さな構造を保存することはできない。
この問題に対する最近の進歩は、CS再構成のための反復的な方向性TV精密化を用いることである。 この方法は2段階あり、第1段階では、与えられた画像のエッジ検出によるノイズの多い点ごとの初期推定値として定義される初期方位磁場を推定し、改良するものである。 第2段階では、方向性TV正則化器を用いて、CS再構成モデルを提示する。 7898>
既存の手法
Iteratively reweighted l 1 {displaystyle l_{1}} (反復的重み付けl 1最小化)。


最小化

CS
constrained l 1 {displaystyle l_{1}}によるCS再構成モデルにおいて、L1最小化法

最小化では、大きな係数はl 1 {displaystyle l_{1}}で大きくペナルティーを受けることになります。

norm. l 1 {displaystyle l_{1}}の重み付き定式化が提案された。

最小化では、非ゼロ係数をより民主的に罰するように設計されている。 適切な重みを構築するために、反復アルゴリズムが使用される。 各反復は、1つのl 1 {displaystyle l_{1}} を解くことを必要とする。

最小化問題は、よりl 0 {displaystyle l_{0}}に近い凹型ペナルティ関数の局所最小を見つけることによって行われる。

norm. 通常、ペナルティ関数曲線の急激な遷移を避けるための追加パラメータが、安定性を確保し、ある反復でゼロ推定が必ずしも次の反復でゼロ推定につながらないように、反復式に導入される。 この方法では、基本的に、次の反復で使用する重みの計算に現在の解を使用する。
長所と短所
初期の反復では不正確なサンプル推定値が見つかるかもしれませんが、この方法は後の段階でこれらをダウンサンプリングして、より小さい非ゼロ信号推定値に重みを与えます。 欠点としては、関数の凹性によりグローバルミニマムが毎回得られるとは限らないので、有効な開始点を定義する必要があることである。 もう一つの欠点は、この方法は、基礎となる画像構造に関係なく、画像勾配に一様にペナルティを与える傾向があることである。 このため、エッジ、特に低コントラスト領域のエッジが過剰に平滑化され、結果として低コントラストの情報が失われることになります。 本手法の利点は、疎な信号に対するサンプリングレートの低減、ノイズや他のアーチファクトの除去に強い画像の再構成、非常に少ない反復回数の使用などです。 また、疎な勾配を持つ画像の復元にも役立ちます。
下図において、P1とは、反復再構成処理の第1段階であるファンビーム形状の射影行列Pを指し、データ忠実度項によって制約される。 これは、正則化が行われていないため、ノイズやアーチファクトを含む可能性がある。 P1の最小化は、共役勾配最小二乗法によって解かれる。 P2は、反復再構成処理の第2段階を意味し、エッジ保存全変動正則化項を利用してノイズやアーチファクトを除去し、再構成画像/信号の品質を向上させるものである。 P2の最小化は単純な勾配降下法によって行われる。 収束は、各反復の後に、f k – 1 = 0 {displaystyle f^{k-1}=0} かどうかを確認することによって、画像の陽性度をテストすることによって決定される。

f k – 1 < 0 {displaystyle f^{k-1}<0} の場合について。

(Note that f {displaystyle f})

は、患者画像の異なるボクセルにおける異なるX線線形減衰係数を意味する)。
Edge-preserving total variation (TV) based compressed sensing

低線量CTで得られた高アンダーサンプルのデータから低い電流レベル(ミリアンペア)によってCT画像を再構成する、縁取りの正則化による反復CT再構成法である。 撮影線量を低減するために、スキャナ検出器で取得するX線投影数を減らすことが一つのアプローチとして用いられている。 しかし、この不十分な投影データでCT画像を再構成すると、ストリーキングアーチファクトが発生する可能性があります。 さらに、標準的なTVアルゴリズムでこの不十分な投影データを使用すると、問題が過小決定されるため、無限に多くの可能な解を導くことになる。 本手法では、元のTVノルムにペナルティ重み付け関数を追加で割り当てる。 これにより、画像中の強度の鋭い不連続性を容易に検出することができ、それによって信号/画像再構成の過程で、回復したエッジ情報を格納するための重みを適応させることができる。 パラメータσ{displaystyle \sigma }は以下の通りです。

は、エッジの画素を非エッジの画素と区別するために適用するスムージングの量を制御します。 σ {displaystyle \sigma }の値は、エッジの画素に適用されるスムージングの量です。

は、σ{displaystyle \sigma }より大きい勾配値を持つ画素が一定割合となるように、勾配の大きさのヒストグラムの値に基づいて適応的に変更されます。

. このため、エッジ保存の全変動項が疎になり、実装が高速化される。 前方-後方分割アルゴリズムとして知られる2段階の反復処理を用いる。 最適化問題は2つのサブ問題に分割され、それぞれ共役勾配最小二乗法と単純勾配降下法で解かれる。 この方法は、望ましい収束が達成されるか、反復回数が最大に達したときに停止されます。
長所と短所
この方法の短所は、再構成された画像に小さい構造がないことと、画像の解像度が低下することである。 しかし、このエッジ保存TVアルゴリズムは、従来のTVアルゴリズムより少ない反復回数で済む。 再構成画像の水平・垂直強度プロファイルを分析すると、エッジ点では鋭いジャンプがあり、非エッジ点では無視できるほど小さな揺らぎがあることがわかる。 このように、本手法はTV法と比較して相対誤差が少なく、高い相関を得ることができる。
Iterative model using a directional orientation field and directional total variation
エッジやテクスチャの詳細の過度の平滑化を防ぎ、ノイズやアーチファクトに対して正確で頑健な再構成CS画像を得るために、この方法を使用した。 まず、画像I {displaystyle I}のノイズの多いポイントワイズ配向フィールドの初期推定を行う。

, d ^ {displaystyle {hat {d}}} 。

, が得られる。 このノイズの多い方位磁場を定義することで、後の段階で方位磁場推定におけるノイズの影響を低減させることができる。 次に、構造テンソルに基づく粗い方位磁場推定を導入し、以下のように定式化する。 J ρ ( ∇ I σ ) = G ρ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) {displaystyle J_{rho }(\nabla I_{sigma })=G_{rho }*(\nabla I_{sigma }otimes \nabla I_{sigma })={begin{pmatrix}J_{11}&J_{12}십J_{12}&J_{22}센터{pmatrix}}} {G_{rho}*(\nabla I_{sigma ]{G_{sigma ]{G_{sigma ]})

. ここで、J ρ {displaystyle J_{rho }} 。

は、標準偏差ρ{displaystyle \rho }を持つ画像画素点(i,j)に関する構造テンソルを意味します。

. G {displaystyle G}

はガウスカーネル ( 0 , ρ 2 ) {displaystyle (0,\rho ^{2})} } のことである。

with standard deviation ρ {displaystyle \rho }.

… σ {displaystyle \sigma }.

は画像Iの手動定義パラメータ{displaystyle I}を指す。

以下では、エッジ検出がノイズに鈍感になる。 ∇ ΣI {displaystyle \nabla I_{sigma }}

は画像のグラデーション I {displaystyle I} のことである。

and ( ∇ I σ ⊗ ∇ I σ ) {displaystyle (\nabla I_{sigma } ◇otimes \nabla I_{sigma })} {Displaystyle (| | | | | | | | | |)

はこの勾配を用いて得られるテンソル積のことである。
得られた構造テンソルをガウシアンカーネルG{displaystyle G}で畳み込む。

σ {displaystyle \sigma } を用いて方位推定精度を向上させるため。

は未知のノイズレベルを考慮し、高い値に設定されている。 画像中の各画素(i,j)に対して、構造テンソルJは対称な正の半正定値行列である。 画像中の全画素をG{displaystyle G}で畳み込む。

, J {displaystyle J}の正規直交固有ベクトルωとυを与える。 
は、d ^ {}displaystyle {hat {d}}} と定義される。

= υとなる。 この推定は強いエッジでは正確である。 しかし、弱いエッジやノイズのある領域では、その信頼性が低下する。
この欠点を克服するために、データ項がノイズの影響を低減して精度を向上させ、L2-ノルムによる第2ペナルティ項が初期粗い推定の精度を保証する忠実度項である、洗練された方向モデルが定義されている。
この方位フィールドは、CS再構成のための方向性全変動最適化モデルに、以下の式で導入される。 m i n X ‖∇ X∙d‖1 + λ 2‖Y – Φ X‖2 2 {displaystyle min_{mathrm {X} } } \lVert \nabla d }{frac {lambda }{2}} } \rVert _{1}+{frac {hatlambda} {2}}}は、この方位磁場をCS再構成のための方向性全変動最適化モデルに導入する。

. X {displaystyle \mathrm {X} } .
は復元すべき目的信号である。 Yは対応する測定ベクトル、dは反復精製方位磁場、Φ {displaystyle \Phi }は対応する測定ベクトルである。

はCS測定行列である。 この方法は数回の反復を経て最終的に収束する。 d ^ { {displaystyle {hat {d}}}

は再構成画像X k – 1の方位磁場近似推定 {displaystyle X^{k-1}} である。

前の反復から(収束とその後の光学性能を確認するために、前の反復を使用する)。 X {displaystyle \mathrm {X} } で表される2つのベクトル場に対して
and d {displaystyle d} {9329>
And

, X ∙ d {displaystyle \mathrm {X} \bullet d} br>

, X ∙ d {displaystyle \mathrm {X} 8733

は、X {displaystyle \mathrm {X} } の水平、垂直ベクトル要素の掛け算を意味します。
and d {displaystyle d} {9329>Thinkmathrm{X} And

と続き、その後に足し算をする。 これらの方程式は一連の凸の最小化問題に還元され、その後、変数分割と拡張ラグランジュ(閉形式の解を持つFFTベースの高速ソルバー)法の組み合わせで解かれる。 この方法(拡張ラグランジュ)は、この方法の収束を保証する分割ブレグマン反復と等価であると考えられている。 方位磁場dは、( d h , d v ) {displaystyle (d_{h},d_{v})} に等しいと定義される。

, ここで d h , d v {displaystyle d_{h},d_{v}} ………………….{d_{h},d_{v}}.

はd {displaystyle d}の水平・垂直方向の推定値を定義しています。

.

方位磁場のためのAugmented Lagrangian法と反復方向磁場精密化モデル
方位磁場のためのAugmented Lagrangian法。 m i n X ‖ ∇ X∙ d‖ 1 + λ 2‖ Y – Φ X‖ 2 2 {displaystyle min_{mathrm {X} } } \lVert \nabla d } }{frac {lambda} }{2}} \lVert Y-‛̮ ‛̮ {{2}^{2}}

╱は、”Min_{mathrm{X}}”であり、これは “Min_{mathrm {X}”であり、”min_{Mathrm {X}”であり、”min_{mathrm{X}”である。 includes initializing d h , d v , H , V {displaystyle d_{h},d_{v},H,V}.

そして、L 1 {displaystyle L_{1}}の近似最小化器を求めます。

これらの変数に関して。 その後、ラグランジュ乗数は更新され、収束が達成された時点で反復プロセスが停止される。 反復方向全変動精密化モデルでは、拡張ラグランジュ法では、X , P , Q , λ P , λ Q {displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}を初期化する必要があります。

・・・・・・・・・・・・・。
Here, H , V , P , Q {displaystyle H,V,P,Q} .

は新たに導入した変数で、H {displaystyle H} とする。

= ∇ d h {displaystyle \nabla d_{h}} }.

, V {displaystyle V} .

= ∇ d v {displaystyle \nabla d_{v}} }.

, P { {displaystyle P}

= ∇ X {displaystyle \nabla {X} } }.

, and Q {displaystyle Q} {displaystyle Q} .

= P ∙ d {displaystyle Pbullet d} {displaystyle Pbullet d} {displaystyle Pbullet d} {displaystyle Pbullet d} = P ∙ d

. λ H , λ V , λ P , λ Q {displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}} ←クリックすると拡大します。

are Lagrangian multipliers for H , V , P , Q {displaystyle H,V,P,Q} ……Lagrangian multipliers for H, V, P, Q

. 各反復において、L 2の近似最小化器{displaystyle L_{2}} が得られる。

with variables ( X , P , Q {displaystyle \mathrm {X} ,P,Q} ]について

)が算出される。 そして、フィールド精密化モデルと同様に、ラグランジュ乗数を更新し、収束した時点で反復処理を停止する。
方位磁場精密化モデルでは、以下のように反復処理でラグランジュ乗数を更新している。
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ( d h ) k ) {displaystyle (\lambda _{H})^{k}=(\lambda _{k-1}+gamma _{H}(H^{k}-atinabla (d_{h})^{k})} } {DISCAMM_H} (H^{k}) ^{k} {d_{h})

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+thegm _{V}(V^{k}-thegm (d_{v})^{k})} } { d_nabla _{V})^{k}=(|d_{k}-thegm (d_{v})){d_nabla (d_{k}))} {displaystyle ( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k)

反復方向性全変動精密化モデルでは、以下のようにLagrangian multipliersを更新しています。
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ( X ) k ) {displaystyle (\lambda _{P})^{k}=(\lambda _{k-1}+gamma _{P}(P^{k}-themenabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ・ d ) {displaystyle (\lambda _{Q})^{k}=(\lambda _{k-1}+gamma _{Q}(Q^{k}-P^{k} ◇double) } } { {Displaystyle ( λQ) )k=(\nabla _{Q})^{k-1} + gamma _{Q}(Q^{k}-P^{k}◇bullet ) ◇Diamond

ここで、(\lambda _{Q}}は、)Q^{k}とQ{{Q}{Q}{Q}{Q}-P^{{kW}}の間に位置する)Q{{Q}{Q}{{Q}{Q γ H , γ V , γ P , γ Q {displaystyle: \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}}

は正の定数である。
長所と短所
ピーク信号対雑音比(PSNR)と構造類似度指数(SSIM)メトリクスとテスト性能のための既知のグランドトゥルース画像に基づいて、反復方向性全変動の方が非反復法よりもエッジとテクスチャ領域を保存する上で優れた再構成性能を持っていると結論づけられている。 この性能向上には,エッジのある領域で方位磁場の整合性を高める一方で,平坦な領域では方向性のない画素を増加させる方位磁場精密化モデルが大きな役割を果たす<7898>.