Learning Objective
1. ある単位から同じ種類の別の単位に変換できる。
2.2項「単位の表現」では、初期単位を同じ種類の別の単位に置き換えて、理解しやすい数値を得る例を示しました。 このセクションでは、そのプロセスを正式に説明します。
簡単な例として、4ヤードには何フィートあるのか考えてみましょう。 ほとんどの人は、ほぼ自動的に「4ヤードに12フィートある」と答えるでしょう。 この判断はどのようになされたのでしょうか。 さて、1 ヤードに 3 フィートあり、4 ヤードあれば、4 × 3 = 12 フィートが 4 ヤードにあります」
これはもちろん正しいのですが、非公式なものです。 より一般的に適用できるように形式化してみましょう。 1ヤード(yd)は3フィート(ft)に等しいことが分かっています:
1 yd = 3 ft
数学では、この式を「等式」と呼びます。 代数学のルールでは、(ゼロで割らない限り)等式を変更(乗算、除算、加算、減算)しても、新しい式は等式であることに変わりはない。 たとえば、両辺を 2 で割ると、
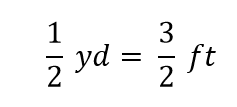
1/2 a yard = 3/2, つまり 1.5 foot となることがわかりますが、これも正しいことがわかっているので、上の式は依然として等式となります。 元の等式に戻り、等式の両辺を 1ヤード(数と単位)で割るとします:
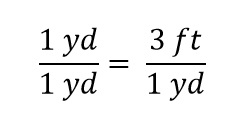
この式も、代数学の規則により、等式であることに変わりはありません。 左の分数は 1 に等しい。 分子と分母に同じ量があるので、1に等しいはずです。
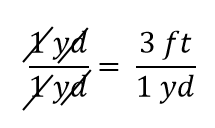
分数の中ですべてがキャンセルされると、分数は 1 に減少します:
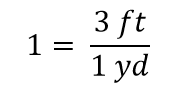
3 ft1 yd という表現があって、これは 1 と同じになります。 これは奇妙な書き方ですが、意味があります。3フィート=1ヤードなので、分子と分母の量は同じ量であり、ただ異なる単位で表現されています。 3 ft1 ydという表現は変換係数と呼ばれ、ある量の単位を別の単位に正式に変更するために使われます。 (3975>
これがどのように起こるかを見るために、元の量から始めましょう:
4 yd
ここでこの量に1を掛けてみましょう。 ただ1を掛けるのではなく、1を3 ft1 ydと書いてみましょう:
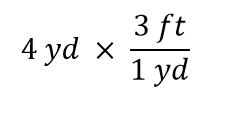
4ydの項は4 yd/1と考えることができ、つまり分母が1である分数と考えることができるのです。 私たちは本質的に分数の掛け算をしているのです。 分数の分子と分母に同じものが現れると、それらは打ち消されます。 この場合、相殺されるのは単位ヤードです。
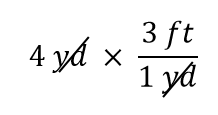
以上が相殺できることです。 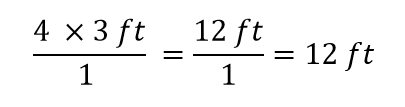
ここでも、最初にやったのと同じように12 ftという答えが出ます。 しかし、この場合、さまざまな問題に適用できる、より正式な手順を使用しました。
14.66 m は何 mm ですか。 これに答えるには、ミリメートルとメートルの間の変換係数を構築し、元の量に正しく適用する必要があります。 まず、ミリメートルの定義ですが、
1 mm = 1/1,000 m
1,000 は接頭語のミリ-が意味するところです。 ほとんどの人は分数を使わない方が楽なので、1,000を反対側の分子に持ってきて、この式を書き直します:
1,000 mm = 1 m
これで、1つの量を両辺に割って変換係数を作りました。 しかし、ここで疑問が生じる。どちらの量で割るのか? 3975>
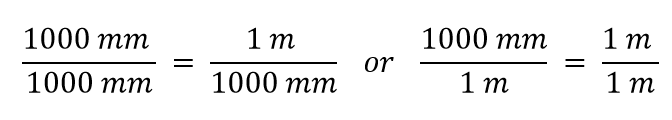
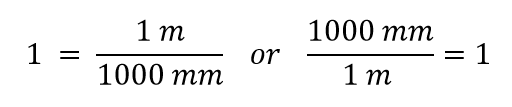
どの変換係数を使うのか? 答えは、最初の数量からどの単位を取り除きたいかによります。 私たちの数量の元の単位はメートルで、それをミリメートルに変換したいのです。 元の単位が分子にあることが前提なので、それを取り除くには、分母にメートルの単位を入れれば、両者は相殺されます。 そこで、2番目の変換係数を使うことにします。 単位をキャンセルして計算すると、
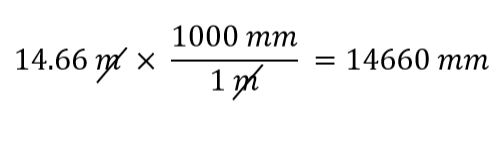
m がキャンセルされて、関心のある単位である mm が残ることに注目してください。
例題7
- 35.9 kLをリットルに変換する。
- 555 nmをメートルに変換する。
解答
-
1kL=1000Lということを利用します。定義できる二つの変換係数のうち、有効なのは1000L/1kLです。 この換算係数を適用すると、
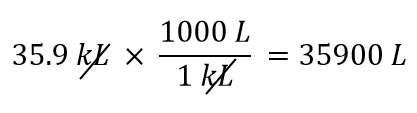
-
1 nm = 1/1,000,000,000 mという事実を利用して、100万nm = 1 m、109 nm = 1 mと書き直せば、2つ考えられる換算係数から分母がnm単位であるものを適切としていることがわかります。 1m/109 nmである。 この変換係数を適用すると、
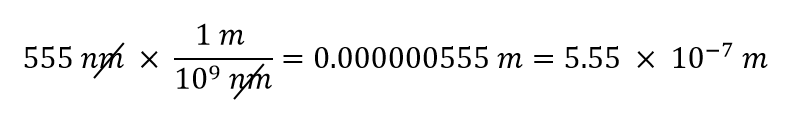
最終ステップで、答えを科学表記で表現します。
自分で試す
- 変換 67.08 μLをリットルに変換する。
- 56.8 mをキロメートルに変換する。
答え
- 6.708 × 10-5 L
- 5.68 × 10-2 km
m2など複数のユニットの積である派生単位を持っていたらどうでしょう? 平方メートルを平方センチメートルに変換したいとします。 重要なのは、m2がm×mを意味すること、つまり、派生単位にメートル単位が2つあることを思い出すことです。 つまり、単位ごとに2つの変換係数が必要なのです。 例えば、17.6 m2を平方センチに変換する場合、次のように変換します:
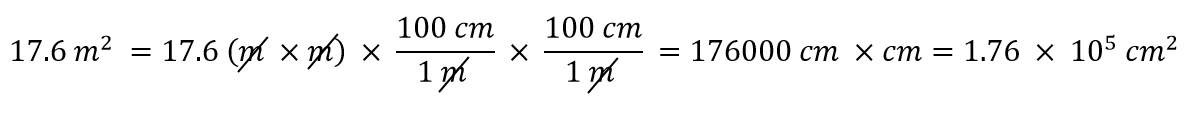
例8
0.6 立方cmは何cmか?883 m3?
解答
指数が3だと、長さの単位が3つあるので、ひいてはメートルとセンチメートルの変換係数を3つ使う必要があるのです。 したがって、
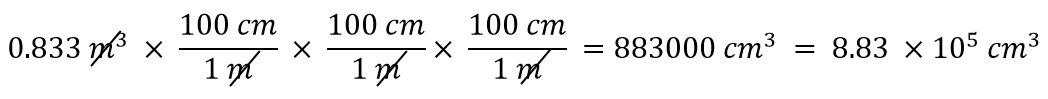
三つのメートル単位が確かに相殺されることを自分で実証してください。
自分で試す
0.0923m3には何立方ミリあるか
答え
9.23 × 107 mm3
変換したい単位が派生単位の分母にあるとしたら、どうでしょうか。 そうすると、変換係数の中で、除去したい単位が分子になければなりません。 そうすると、分母にある元の単位と相殺され、分母に新しい単位が導入されます。
例題9
88.4m/minをメートル/秒に変換する
解答
分母の単位を分から秒に変えたいと思います。 1分間に60秒あるので(60秒=1分)、外したい単位である分が分子になるように変換係数を組みます。 3975>
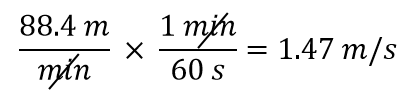
88.4 が自動的に分子に入ることに注意してください。 これは、どんな数字も 1 で割った分数の分子になると考えることができるからです。
自分でテスト
0.203 m/min をメートル/秒に変換する
答え
0.00338 m/s または 3.38 × 10-3 m/s
図 2.8 How Fast Is Fast?

ソースはこちら。 “Grapevine snail “by Jürgen Schoneris licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.