Sono processi di apprendimento stocastico con struttura ricorrente e sono la base delle prime tecniche di ottimizzazione usate in ANN. La macchina di Boltzmann è stata inventata da Geoffrey Hinton e Terry Sejnowski nel 1985. Più chiarezza può essere osservata nelle parole di Hinton su Boltzmann Machine.
“Una caratteristica sorprendente di questa rete è che usa solo informazioni disponibili localmente. Il cambiamento di peso dipende solo dal comportamento delle due unità che connette, anche se il cambiamento ottimizza una misura globale” – Ackley, Hinton 1985.
Alcuni punti importanti sulla macchina di Boltzmann –
-
Utilizzano una struttura ricorrente.
-
Sono composti da neuroni stocastici, che hanno uno dei due stati possibili, o 1 o 0.
-
Alcuni dei neuroni in questo sono adattivi (stato libero) e alcuni sono bloccati (stato congelato).
-
Se applichiamo l’annealing simulato sulla rete Hopfield discreta, allora diventerebbe una macchina di Boltzmann.
Obiettivo della macchina di Boltzmann
Lo scopo principale della macchina di Boltzmann è di ottimizzare la soluzione di un problema. È il lavoro della macchina di Boltzmann di ottimizzare i pesi e le quantità relative a quel particolare problema.
Architettura
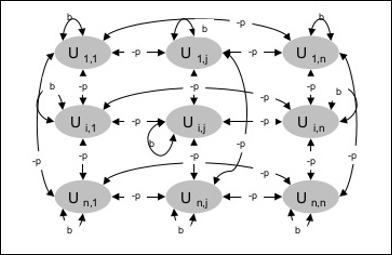
Il seguente diagramma mostra l’architettura della macchina di Boltzmann. È chiaro dal diagramma che si tratta di una matrice bidimensionale di unità. Qui, i pesi delle interconnessioni tra le unità sono -p dove p > 0. I pesi delle autoconnessioni sono dati da b dove b > 0.
Algoritmo di allenamento
Come sappiamo che le macchine di Boltzmann hanno pesi fissi, quindi non ci sarà nessun algoritmo di allenamento in quanto non è necessario aggiornare i pesi nella rete. Tuttavia, per testare la rete dobbiamo impostare i pesi e trovare la funzione di consenso (CF).
La macchina di Boltzmann ha un insieme di unità Ui e Uj e ha connessioni bidirezionali su di esse.
-
Consideriamo il peso fisso diciamo wij.
-
wij ≠ 0 se Ui e Uj sono connessi.
-
Esiste anche una simmetria nell’interconnessione pesata, cioè.cioè wij = wji.
-
esiste anche wii, cioè ci sarebbe l’autoconnessione tra unità.
-
Per ogni unità Ui, il suo stato ui sarebbe o 1 o 0.
L’obiettivo principale della Macchina di Boltzmann è quello di massimizzare la Funzione di Consenso (CF) che può essere data dalla seguente relazione
$$CF\:=:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$
Ora, quando lo stato cambia da 1 a 0 o da 0 a 1, allora il cambiamento nel consenso può essere dato dalla seguente relazione –
$$Delta CF\:==(1\:-\:2u_{i})(w_{ij}\:+:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Qui ui è lo stato corrente di Ui.
La variazione del coefficiente (1 – 2ui) è data dalla seguente relazione –
$$$(1\\:-\:2u_{i})\\\:=\begin{cases}+1, & U_{i}\:è\:currently\:off\\\-1, & U_{i}:è\:attualmente\:on\ fine{casi}$$
Generalmente, l’unità Ui non cambia il suo stato, ma se lo fa allora l’informazione sarebbe residente localmente all’unità. Con questo cambiamento, ci sarebbe anche un aumento del consenso della rete.
La probabilità della rete di accettare il cambiamento di stato dell’unità è data dalla seguente relazione –
$$AF(i,T)\\\:=\frac{1}{1\:+\:exp}$
Qui, T è il parametro di controllo. Diminuirà man mano che CF raggiunge il valore massimo.
Algoritmo di test
Passo 1 – Inizializza quanto segue per iniziare la formazione –
- Pesi che rappresentano il vincolo del problema
- Parametro di controllo T
Passo 2 – Continua i passi 3-8, quando la condizione di arresto non è vera.
Passo 3 – Eseguire i passi 4-7.
Passo 4 – Supporre che uno degli stati abbia cambiato il peso e scegliere l’intero I, J come valori casuali tra 1 e n.
Passo 5 – Calcolare il cambiamento nel consenso come segue –
$$Delta CF:=\(1\:-\:2u_{i})(w_{ij}:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Passo 6 – Calcolare la probabilità che questa rete accetti il cambiamento di stato
$$AF(i,T)\:=\frac{1}{1\:+\:exp}$
Step 7 – Accettare o rifiutare questo cambiamento come segue –
Caso I – se R < AF, accettare il cambiamento.
Caso II – se R ≥ AF, rifiutare la modifica.
Qui, R è il numero casuale tra 0 e 1.
Step 8 – Ridurre il parametro di controllo (temperatura) come segue –
T(nuovo) = 0.95T(vecchio)
Step 9 – Testare le condizioni di arresto che possono essere le seguenti –
- La temperatura raggiunge un valore specificato
- Non c’è cambiamento di stato per un numero specificato di iterazioni