Bravais-roosters

Wetenschap > Scheikunde >Vaste Stof > Bravais-roosters

In dit artikel zullen we de structuren van Bravais-roosters bestuderen.

Een kristal is een homogeen deel van een vaste stof dat bestaat uit een regelmatig patroon van structurele eenheden die met elkaar verbonden zijn door vlakke oppervlakken die een bepaalde hoek met elkaar maken.

Eenheidscel:

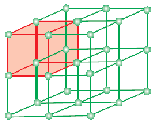
Een eenheidscel is de kleinste structurele repeterende eenheid van een kristallijne vaste stof (ruimtelrooster). Wanneer eenheidscellen van dezelfde kristallijne stof zich in de ruimte in alle richtingen herhalen, wordt een kristallijne vaste stof gevormd. De eenheidscel wordt op papier voorgesteld door lijnen te trekken die de middelpunten van de samenstellende deeltjes met elkaar verbinden.

De geometrische vorm die alleen bestaat uit een regelmatige reeks punten in de ruimte wordt raster of ruimtelat genoemd. Het kan worden gedefinieerd als een reeks punten die laten zien hoe moleculen, atomen of ionen zijn gerangschikt op verschillende plaatsen in een driedimensionale ruimte. Elk punt op het snijpunt van lijnen in de eenheidscel vertegenwoordigt een constituerend deeltje, namelijk een molecuul, atoom of ion. Dit snijpunt van lijnen in de eenheidscel wordt roosterpunt of roosterplaats genoemd.

Noot: Elk roosterpunt in het kristalrooster heeft dezelfde omgeving of milieu. Twee of meer kristallijne substanties kunnen dezelfde roosterruimte hebben. Elk deeltje in de matrix wordt altijd vertegenwoordigd door een roosterpunt in de driedimensionale matrix.

Karakteristieken van kristalrooster:

• Het kristalrooster is een regelmatige ordening van samenstellende deeltjes van een kristallijne vaste stof in de driedimensionale ruimte.
• Het bestaat uit een groot aantal eenheidscellen.
• Het kristalrooster wordt gedefinieerd in termen van eigenschappen van de eenheidscel.
• Bij het uiteenvallen vormt het een groot aantal eenheidscellen.
• Een kristalrooster kan tijdens experimenten in een laboratorium worden verkregen, behandeld en bestudeerd.
• Het is een macroscopische eigenschap.

Karakteristieken van Eenheidscel:

• Eenheidscel is de kleinste structurele repeterende eenheid van kristallijne vaste stof.
• Het is de fundamentele eenheid van kristalrooster die alle eigenschappen van het kristal bezit.
• Eenheidscel definieert fundamentele eigenschappen kristalrooster.
• Eenheidscellen zijn een fundamentele eenheid, vandaar kan niet verder worden verdeeld.
• Eenheidscel is hypothetisch concept Vandaar dat het niet kan worden verkregen tijdens experimenten.
• Het is een microscopische eigenschap.

Typen Ruimtelatten:

Eendimensionale roosters:

In dit rooster bestaat een verzameling punten die op gelijke afstanden langs.

Twee-dimensionale rasters:

In dit type zijn twee zijden en de hoek tussen beide gespecificeerd. Er zijn vijf soorten tweedimensionale rasters.

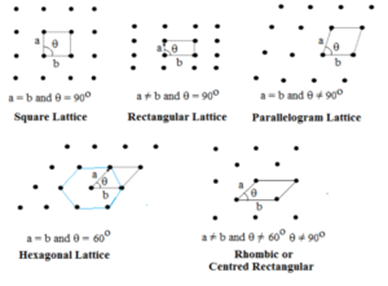
Hexagonaal raster is een ruit met θ = 60°

Bravais-rasters:

Laat de lengten van drie zijden van de eenheidscel a, b, en c zijn. Zij α de hoek tussen zijde b en c. Zij β de hoek tussen zijden a en c. Zij γ de hoek tussen zijden a en b.

De Franse wiskundige Bravais zei dat voor verschillende waarden van a, b, c, en α, β, γ, maximaal veertien (14) structuren mogelijk zijn. Deze ordeningen worden Bravais-rasters genoemd.

14 Bravais-rasters:

Sr. No.	Kristal Systeem	Ruimte-rooster Type	Diagram	Randlengten	Hoeken	Voorbeelden
	Kubiek	Eenvoudig primitief		a = b = c	α = β = γ = 90°	Polonium (Po)
	Kubisch	Lichaam gecentreerd		a = b = c	α = β = γ = 90°	Iron (Fe), Rubidium (Rb), Natrium (Na), Titanium (Ti), Tungsten (W), Uranium (U), Zirkonium (Zr)
	Cubic	Face centred		a = b = c	α = β = γ = 90°	Koper (Cu), Aluminium (Al), Nikkel (Ni), Goud (Au), Zilver (Ag), Platina (Pt)
	Tetragonal	Simple primitief		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonaal	Lichaam gecentreerd		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombisch	Eenvoudig primitief		a ≠ b ≠ c	α = β = γ = 90°	Rhombisch zwavel
	Orthorhombisch	Lichaam gecentreerd		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombisch	Face gecentreerd		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Orthorhombisch	Eind gecentreerd		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monoklien	eenvoudig primitief		a ≠ b ≠ c	α =γ = 90° en β ≠ 90°	Monokliene zwavel
	Monokliene	Eind gecentreerd		a ≠ b ≠ c	α =γ = 90° en β ≠ 90	Na2SO4. 10H2O
	Triclinisch	simpel primitief		a ≠ b ≠ c	α =γ = 90° en β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonaal	Eenvoudig primitief		a = b ≠ c	α = β = 90° en γ = 120°	ZnO, BeO, CoS, SnS
	Rhombohedral	Simple primitive		a ≠ b ≠ c	α = β = γ ≠ 90°	Calciet, NaNO3, FeCO3

Deeltje op hoek:

Het deeltje op de hoek van de eenheidscel wordt gedeeld door 8 eenheidscellen (4 lagen onder en 4 lagen boven). Dus elke eenheidscel 1/8 deeltje.

Deeltje aan voorkant:

Het deeltje aan de voorkant van de eenheidscel wordt gedeeld door 2 aangrenzende eenheidscellen. Vandaar dat elk eenheidscel 1/2 deeltje.

Deeltje aan de rand:

Het deeltje aan de rand van de eenheidscel wordt gedeeld door 4 eenheidscellen (2 lagen eronder en 2 lagen erboven). Vandaar dat elke eenheidscel 1/4 deeltje is.

Coördinatiegetal:

Het coördinatiegetal van de samenstellende deeltjes van het kristalrooster is het aantal deeltjes dat een enkel deeltje in een kristalrooster omringt.

Meer coördinatiegetal betekent dat de deeltjes dichter opeengepakt zitten in het kristalrooster. Coördinatiegetal is de maat voor de hardheid van het kristal.

Aantal deeltjes in eenheidscel en coördinatiegetal

Eenvoudige kubische structuur (scc):

Uit de structuur kunnen we afleiden dat er 8 deeltjes op 8 hoeken van de eenheidscel zijn.Elk hoekdeeltje wordt gedeeld door 8 naburige eenheidscellen. Elke eenheidscel bevat dus 1/8 deel van het deeltje op zijn hoek.
Aantal hoekpunten = 8, dus aantal deeltjes in eenheidscel = 1/8x 8 = 1

Elk deeltje in deze structuur staat direct in contact met vier andere deeltjes in zijn vlak en met telkens één deeltje in de laag erboven en de laag eronder. Het coördinatiegetal voor de eenvoudige kubische structuur is 4+ 1+ 1 = 6

Body-Centred Cubic Structure (bcc):

Uit de structuur kunnen we afleiden dat er 8 deeltjes op 8 hoeken van de eenheidscel zijn.Elk hoekpartikeltje wordt gedeeld door 8 aangrenzende eenheidscellen. Elke eenheidscel bevat dus 1/8e van de deeltjes op zijn hoek. Aantal hoeken = 8, dus aantal deeltjes in eenheidscel op hoeken = 1/8 x 8 = 1

Op hetzelfde moment is er een atoom in het centrum van de cel, Vandaar het aantal deeltjes in eenheidscel 1 + 1 = 2

Elk deeltje in deze structuur is direct in contact met vier andere deeltjes in de laag erboven en vier deeltjes in de laag eronder. Vandaar dat het coördinatiegetal voor de lichaamsgecentreerde kubische structuur 4 + 4 = 8

Gecentreerde kubische structuur (fcc):

Uit de structuur kunnen we afleiden dat er 8 deeltjes op 8 hoeken van de eenheidscel zijn. Elk hoekdeeltje wordt gedeeld door 8 andere aangrenzende eenheidscellen. Elke eenheidscel bevat dus 1/8e van de deeltjes op zijn hoek. Het aantal hoeken = 8. Vandaar dat het aantal partikels in een eenheidscel op de hoeken = 1/8 x 8 = 1

Er zijn 6 partikels op 6 vlakken van de eenheidscel. Elk vlakdeeltje wordt gedeeld door 2 aangrenzende eenheidscellen. Elke eenheidscel bevat dus 1/2 van de deeltjes op zijn zijvlak.
Het aantal zijvlakken = 6. Vandaar het aantal deeltjes op zijvlak = 1/2 x 6 = 3

Hieruit volgt aantal deeltjes in eenheidscel 1 + 3 = 4

Elk deeltje in deze structuur staat in direct contact met 4 andere deeltjes in zijn laag en met 4 deeltjes in de laag erboven en 4 deeltjes in de laag eronder. Het coördinatiegetal voor een gecentreerde kubische structuur is dus 4 + 4 + 4 = 12

Noten:

Voor gecentreerde deeltjes aan de rand wordt het gedeeld door 4 eenheidscellen. Elke eenheidscel bestaat dus uit 1/4 deeltje. Het aantal atomen per eenheidscel is in dezelfde verhouding als de stoichiometrie van de verbinding. Het helpt dus om de formule van de verbinding te voorspellen.

Wetenschap > Scheikunde > Vaste stof > Bravais-roosters