Kryształy Bravais’a

Nauka >Chemia >Ciało stałe >Kryształy Bravais’a

W tym artykule będziemy badać struktury krystalitów Bravais’a.

Kryształ to jednorodna część substancji stałej zbudowana z regularnego układu jednostek strukturalnych połączonych płaszczyznami tworzącymi ze sobą określony kąt.

Komórka jednostkowa:

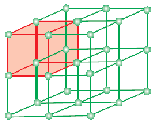
Komórka jednostkowa jest najmniejszą strukturalną powtarzającą się jednostką krystalicznego ciała stałego (siatka przestrzenna). Gdy komórki jednostkowe tej samej substancji krystalicznej powtarzają się w przestrzeni we wszystkich kierunkach, powstaje krystaliczne ciało stałe. Komórka jednostkowa jest reprezentowana na papierze przez rysowanie linii łączących środki cząstek składowych.

Forma geometryczna składająca się tylko z regularnego układu punktów w przestrzeni nazywana jest siatką lub siatką przestrzenną. Może być zdefiniowany jako układ punktów pokazujących, jak cząsteczki, atomy lub jony są rozmieszczone w różnych miejscach, w przestrzeni trójwymiarowej. Każdy punkt na przecięciu linii w komórce reprezentuje cząsteczkę składową, tj. molekułę, atom lub jon. Thispoint of intersection of lines in the unit cell is called lattice point orlattice site.

Note: Each lattice point in the crystal lattice has the samesurroundings or environment. Dwa lub więcej substancji krystalicznej może mieć thesame przestrzeni lattice. Each and every particle in the array is always representedby a lattice point in the three-dimensional array.

Characteristics of Crystal Lattice:

• The crystal lattice is a regular arrangement of constituent particles of a crystalline solid in three-dimensional space.
• It consists of a large number of unit cells.
• Sieć krystaliczną definiuje się pod względem właściwości komórki jednostkowej.
• Przy rozpadzie tworzy liczne komórki jednostkowe.
• Sieć krystaliczna może być otrzymywana, obrabiana i badana w laboratorium podczas eksperymentów.
• Jest to własność makroskopowa.

Charakterystyka komórki jednostkowej:

• Komórka jednostkowa jest najmniejszą strukturalną powtarzającą się jednostką ciała stałego krystalicznego.
• Jest to podstawowa jednostka sieci krystalicznej, która posiada wszystkie właściwości kryształu.
• Komórka jednostkowa określa podstawowe właściwości sieci krystalicznej.
• Komórki jednostkowe są jednostką podstawową, stąd nie mogą być dalej dzielone.
• Komórka jednostkowa jest pojęciem hipotetycznym Stąd nie można jej uzyskać podczas eksperymentów.
• Jest to właściwość mikroskopowa.

Typy kratownic przestrzennych:

Jednowymiarowa kratownica:

W tej kratownicy istnieje zbiór punktów rozmieszczonych w równych odległościach wzdłuż.

Siatka dwuwymiarowa:

W tym typie określone są dwa boki i kąt między nimi. Istnieje pięć typów kratownic dwuwymiarowych.

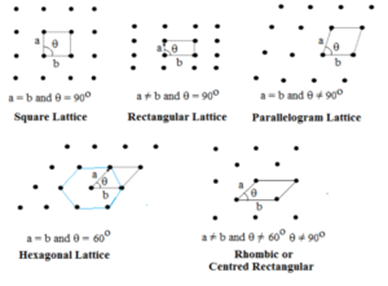
Siatka sześciokątna jest rombem z θ = 60°

Siatki Bravais’a:

Długości trzech krawędzi komórki jednostkowej niech będą a, b i c. Niech α będzie kątem między bokiem b i c. Niech β będzie kątem między bokiem a i c. Niech γ będzie kątem między bokiem a i b.

Matematyk francuski Bravais stwierdził, że dla różnych wartości a, b, c, i α, β, γ, możliwe jest maksymalnie czternaście (14) struktur. Układy te nazywamy kratownicami Bravais’a.

14 kratownic Bravais’a:

.

.

.

.

.

.

.

.

Sr. No.	Kryształ System	Latryca przestrzenna Typ	Diagram	Długości krawędzi	Kąty	Przykłady
	Kubica	Simple prymitywny .		a = b = c	α = β = γ = 90°	Polonium (Po)
	Kostka	Ciało wyśrodkowane		a = b = c	α = β = γ = 90°	Żelazo (Fe), Rubid (Rb), Sód (Na), Tytan (Ti), Tungsten (W), Uran (U), Cyrkon (Zr)
	Kubiczny	Wyśrodkowany		a = b = c	α = β = γ = 90°	Miedź (Cu), Aluminium (Al), Nikel (Ni), Złoto (Au), Srebro (Ag), Platyna (Pt)
	Tetragonal	Simple . prymitywny		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonal	Ciało centrowane		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombic	Simple . prymitywny		a ≠ b ≠ c	α = β = γ = 90°	α = β = γ = 90°		.	Rhombiczna siarka
	Orthorhombiczna	Ciało wyśrodkowane		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombic	Twarz wyśrodkowane		a ≠ b ≠ c	α = β = γ = 90°	.	BaSO4
	Orthorhombic	End centred	End centred		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monokliniczny	simple . prymitywny		a ≠ b ≠ c	α =γ = 90° i β ≠ 90°	.	Monokliniczna siarka
	Monokliniczna	Koniec wyśrodkowany		a ≠ b ≠ c	α =γ = 90° i β ≠ 90	Na2SO4. 10H2O
	Triclinic	simple primitive		a ≠ b ≠ c	α =γ = 90° i β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonal	Simple primitive		a = b ≠ c	α = β = 90° i γ = 120°	ZnO, BeO, CoS, SnS
	Rhombohedral	Simple primitive .		a ≠ b ≠ c	α = β = γ ≠ 90°	Kalcyt, NaNO3, FeCO3

Cząstka w narożniku:

Cząstka w rogu komórki jednostkowej jest wspólna dla 8 komórek jednostkowych (4 warstwy poniżej i 4 warstwy powyżej). Stąd każda komórka jednostkowa 1/8 cząstki.

Particle at Face:

Cząstka na powierzchni komórki jednostkowej jest dzielona przez 2 sąsiednie komórki jednostkowe. Stąd każda komórka jednostkowa 1/2 cząstki.

Cząstka na krawędzi:

Cząstka na krawędzi komórki jednostkowej jest dzielona przez 4 komórki jednostkowe (2 warstwy poniżej i 2 warstwy powyżej). Stąd każda komórka jednostkowa 1/4 cząstki.

Liczba koordynacyjna:

Liczba koordynacyjna cząstki składowej sieci krystalicznej jest to liczba cząstek otaczających pojedynczą cząstkę w sieci krystalicznej.

Większa liczba koordynacyjna powoduje, że cząstki są ciaśniej upakowane w sieci krystalicznej. Liczba koordynacyjna jest miarą twardości kryształu.

Liczba cząstek w komórce jednostkowej i liczba koordynacyjna

Simple Cubic Structure (scc):

Z struktury, możemy zobaczyć, że istnieje 8 cząstek na 8 rogach komórki jednostkowej.Każda cząstka narożna jest dzielona przez 8 sąsiednich komórek jednostkowych. Stąd każda komórka zawiera 1/8 cząstki w swoim rogu.
Liczba rogów = 8, stąd liczba cząstek w komórce = 1/8x 8 = 1

Każda cząstka w tej strukturze jest w bezpośrednim kontakcie z czterema innymi cząstkami w jej płaszczyźnie i po jednej cząstce w warstwie powyżej i poniżej. Liczba koordynacyjna Henceta dla prostej struktury sześciennej wynosi 4+ 1+ 1 = 6

Struktura sześcienna centrowana ciałem (bcc):

Z tej struktury widać, że w 8 narożnikach komórki jednostkowej znajduje się 8 cząstek.Każda narożna cząstka jest dzielona przez 8 sąsiednich komórek jednostkowych. Stąd każda komórka jednostkowa zawiera 1/8 th cząsteczki w swoim rogu. Liczba narożników = 8, stąd liczba cząsteczek w komórce jednostkowej w narożnikach = 1/8 x 8 = 1

W tym samym czasie w centrum komórki znajduje się atom, stąd liczba cząsteczek w komórce jednostkowej 1 + 1 = 2

Każda cząsteczka w tej strukturze styka się bezpośrednio z czterema innymi cząsteczkami w warstwie powyżej i czterema cząsteczkami w warstwie poniżej. Stąd liczba koordynacji dla struktury sześciennej ze środkiem ciała wynosi 4 + 4 = 8

Struktura sześcienna ze środkiem twarzy (fcc):

Z tej struktury widać, że w 8 narożnikach komórki jednostkowej znajduje się 8 cząstek. Każda cząstka narożna jest współdzielona przez 8 innych sąsiednich komórek jednostkowych. Stąd każda komórka jednostkowa zawiera 1/8 th cząsteczki w swoim rogu. Liczba narożników = 8. Stąd liczba cząstek w komórce jednostkowej w narożnikach = 1/8 x 8 = 1

Na 6 ścianach komórki jednostkowej znajduje się 6 cząstek. Każda cząstka na ścianie jest wspólna dla 2 sąsiednich komórek. Stąd każda komórka zawiera 1/2 cząsteczki na jej powierzchni.
Liczba powierzchni = 6. Stąd liczba cząsteczek na powierzchni = 1/2 x 6 = 3

Stąd liczba cząsteczek w komórce 1 + 3 = 4

Każda cząsteczka w tej strukturze styka się bezpośrednio z 4 innymi cząsteczkami w swojej warstwie oraz z 4 cząsteczkami w warstwie powyżej i 4 cząsteczkami w warstwie poniżej. Stąd liczba koordynacji dla struktury sześciennej facecentred wynosi 4 + 4 + 4 = 12

Uwagi:

Dla cząstki centrowanej na krawędziach jest ona dzielona przez 4 komórki jednostkowe. Stąd każda komórka składa się z 1/4 cząsteczki. Liczba atomów w komórce jest w tym samym stosunku co stechiometria związku. Stąd pomaga to przewidzieć wzór związku.

Nauka >Chemia >Stan stały >Siatki Bravaisa