Centros Triangulares

Onde está o centro de um triângulo?

Existem na verdade milhares de centros!

Aqui estão os 4 mais populares:

Centroid, Circumcenter, Incenter e Orthocenter

Para cada um deles, o “centro” é onde as linhas especiais se cruzam, por isso tudo depende dessas linhas!

Vejamos cada uma delas:

Centroid

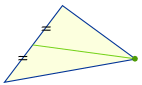Desenhar uma linha (chamada “mediana”) de cada canto até ao ponto médio do lado oposto. Onde as três linhas se cruzam é o centróide, que é também o “centro de massa”:

Tenta isto: corta um triângulo de cartão, desenha as medianas. Será que todos eles se encontram num ponto? Você consegue equilibrar o triângulo nesse ponto?

Circuncentro

>

>

>

>

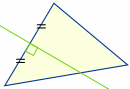Traçar uma linha (chamada “bissetriz perpendicular”) em ângulos rectos até ao ponto médio de cada lado. Onde as três linhas se cruzam é o centro da “circunferência” de um triângulo, chamada “circuncentro”:

Tente isto: arraste os pontos acima até obter um triângulo direito (só de olho está OK). Onde está o circuncentro? Porquê?

Incentro

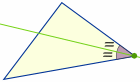>	Traçar uma linha (chamada “bissetriz do ângulo”) de um canto de forma a dividir o ângulo ao meio Onde as três linhas se intersectam é o centro da “circunferência” de um triângulo, chamada “incentro”:

Tenta isto: encontra o incentro de um triângulo usando uma bússola e uma linha recta em: Inscrição de um círculo num triângulo

Orthocenter

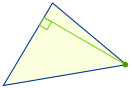Traçar um segmento de linha (chamado “altitude”) em ângulo recto para um lado que vai para o canto oposto. Onde as três linhas se intersectam é o “orthocenter”:

Nota que às vezes as bordas do triângulo têm que ser estendidas fora do triângulo para desenhar as altitudes. Então o orthocenter também está fora do triângulo.