Ciência > Química > Estado Sólido >Treliças Bravais
Neste artigo, estudaremos as estruturas das Treliças Bravais.
Um cristal é uma porção homogênea de uma substância sólida feita de um padrão regular de unidades estruturais unidas por superfícies planas fazendo um ângulo definido entre si.
Unidade Célula:
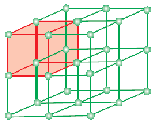
Uma unidade célula é a menor unidade de repetição estrutural de sólido cristalino (malha espacial). Quando células unitárias da mesma substância cristalina são repetidas no espaço em todas as direções, um sólido cristalino é formado. A célula unitária é representada no papel através de linhas que ligam os centros das partículas constituintes.
A forma geométrica consiste apenas numa matriz regular de pontos no espaço é denominada malha ou grelha espacial. Pode ser definida como uma matriz de pontos que mostra como as moléculas, átomos ou íons estão dispostos em diferentes locais, no espaço tridimensional. Cada ponto na intersecção de linhas na célula da unidade representa uma partícula constituinte, ou seja, uma molécula ou átomo ou íon. Este ponto de intersecção de linhas na célula da unidade é chamado de ponto de malha local.
Nota: Cada ponto de malha na malha de cristal tem o mesmo entorno ou ambiente. Duas ou mais substâncias cristalinas podem ter o mesmo espaço na grelha. Cada partícula na matriz é sempre representada por um ponto da malha na matriz tridimensional.
Características da Malha Cristal:
- A malha cristalina é um arranjo regular de partículas constituintes de um sólido cristalino no espaço tridimensional.
- Consiste em um grande número de células unitárias.
- A grelha cristalina é definida em termos de propriedades da célula unitária.
- Em decomposição, forma numerosas células unitárias.
- Uma grelha cristalina pode ser obtida, manuseada e estudada em laboratório durante experiências.
- É uma propriedade macroscópica.
Característica da célula unitária:
- Uma célula unitária é a menor unidade de repetição estrutural de sólido cristalino.
- É a unidade fundamental da malha cristalina que possui todas as propriedades do cristal.
- Célula unitária define propriedades fundamentais da malha cristalina.
- Célula unitária é uma unidade fundamental, portanto não pode ser dividida mais.
- Célula unitária é um conceito hipotético Portanto não pode ser obtida durante experimentos.
- É uma propriedade microscópica.
Tipos de Malha Espacial:
Uma Malha Dimensional:
Nesta malha, existe um conjunto de pontos dispostos a distâncias iguais ao longo.
>

Duas Treliças Dimensionais:
Neste tipo, são especificados dois lados e o ângulo entre eles. Existem cinco tipos de Treliça Bidimensional.
>
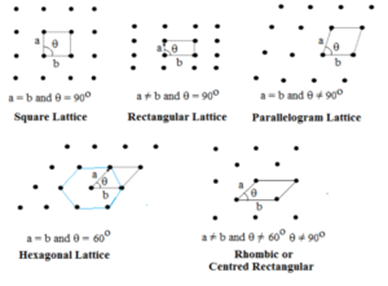
Treliça Sextavada é um losango com θ = 60°
>
Treliças Brancas:
>
 >
>>
>
Deixe comprimentos de três arestas da unidade de célula serem a, b, e c. Que α seja o ângulo entre os lados b e c. Que β seja o ângulo entre os lados a e c. Que γ seja o ângulo entre os lados a e b.
>
O matemático francês Bravais disse que para diferentes valores de a, b, c, e α, β, γ, são possíveis no máximo catorze (14) estruturas. Estes arranjos são chamados de Bravais Lattices.
14 Bravais Lattices:
|
Sr. No. |
Crystal Sistema |
Treliça Espacial Tipo |
Diagrama |
Edge Lengths |
Angles |
Exemplos |
|
Cubic |
Simples primitivo |
 |
a = b = c |
α = β = γ = 90° |
Polonium (Po) |
|
|
Cubic |
Corpo centrado |
 |
a = b = c |
α = β = γ = 90° |
Iron (Fe), Rubidium (Rb), Sódio (Na), Titanium (Ti), Tungsténio (W), Uranio (U), Zircónio (Zr) |
|
|
Cubic |
>
Face centrado |
 |
a = b = c |
α = β = γ = 90° |
Cobre (Cu), Alumínio (Al), Níquel (Ni), Ouro (Au), Prata (Ag), Platina (Pt) |
|
|
Tetragonal |
Simples primitivo |
 |
a = b ≠ c |
α = β = γ = 90° |
SnO2 |
|
|
Tetragonal |
Corpo centred |
 |
a = b ≠ c |
α = β = γ = 90° |
Ti, O2, CaSO4 |
|
|
Orthorhombic |
Simples primitivo |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
Sulfuro lombico |
|
|
Arthorhombic |
>
Corpo centrado |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
KNO3 |
|
| > |
Orthorhombic > |
>
Face centrado |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
BaSO4 |
| > |
Ortobólico |
>
Centrado final > |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
MgSO4, 7H2O |
|
Monoclínico > |
simples primitivo |
 |
a ≠ b ≠ c |
α =γ = 90° e β ≠ 90° |
Enxofre monoclínico |
|
| > |
Monoclínico > |
>
Centrado final |
 |
a ≠ b ≠ c |
α =γ = 90° e β ≠ 90 |
Na2SO4. 10H2O |
|
Triclinic |
simples primitivo |
 |
a ≠ b ≠ c |
α =γ = 90° e β ≠ 90° |
K2Cr2O7, H3BO3 |
|
|
Hexagonal |
Simples primitivo |
 |
a = b ≠ c |
α = β = 90° > e γ = 120° |
ZnO, BeO, CoS, SnS |
|
|
Rhomboédrico |
Simples primitivo |
 |
a ≠ b ≠ c |
α = β = γ ≠ 90° |
Calcite, NaNO3, FeCO3 |
Partícula no canto:
>

A partícula no canto da célula da unidade é partilhada por 8 células unitárias (4 camadas abaixo e 4 camadas acima). Assim cada célula unitária 1/8 partícula.
Partícula na face:

A partícula na face da célula unitária é compartilhada por 2 células unitárias adjacentes. Daí cada unidade de célula 1/2 partícula.
Partícula na borda da célula:

A partícula na borda da unidade de célula é compartilhada por 4 unidades de célula (2 camadas abaixo e 2 camadas acima). Assim, cada célula unitária 1/4 de partícula.
Número de coordenação:
Número de coordenação da partícula constituinte da malha de cristal é então o número de partículas ao redor de uma única partícula em uma malha de cristal.
Mais o número de coordenação mais apertado as partículas são embaladas na malha de cristal. O número de coordenação é a medida da dureza do cristal.
Número de partículas na unidade de célula e número de coordenação
Simples Cubic Structure (scc):

A partir desta estrutura, podemos ver que existem 8 partículas em 8 cantos da unidade de célula. Assim cada célula contém 1/8 da partícula em seu canto.
Número de cantos = 8, Assim o número de partículas na célula = 1/8x 8 = 1
Cada partícula nesta estrutura está diretamente em contato com quatro outras partículas em seu plano e uma partícula cada na camada acima e a camada abaixo. Hencethe número de coordenação da estrutura cúbica simples é 4+ 1+ 1 = 6

Estrutura Cúbica Centrada no Corpo (bcc):

A partir desta estrutura, podemos ver que existem 8 partículas em 8 cantos da célula unitária.Cada partícula de canto é compartilhada por 8 células de unidade vizinhas. Assim, cada célula contém 1/8 da partícula em seu canto. Número de cantos = 8,daí o número de partículas na célula unitária nos cantos = 1/8 x 8 = 1
Ao mesmo tempo, há um átomo no centro da célula, daí o número de partículas na célula unitária 1 + 1 = 2
Cada partícula nesta estrutura está diretamente em contato com quatro outras partículas na camada acima e quatro partículas na camada abaixo. Assim o número de coordenadas da estrutura cúbica centrada no corpo é 4 + 4 = 8

Estrutura Cúbica Centrada na Face (fcc):

Da estrutura, podemos ver que há 8 partículas em 8 cantos da célula unitária. Cada partícula de canto é compartilhada por 8 outras células de unidade vizinhas. Assim, cada célula contém 1/8 da partícula em seu canto. O número de cantos = 8. Daí o número de partículas em uma célula unitária nos cantos = 1/8 x 8 = 1
Existem 6 partículas em 6 faces da célula unitária. Cada partícula de face é compartilhada por 2 células da unidade vizinha. Daí que cada célula contém 1/2 das partículas em face.
O número de faces = 6. Daí o número de partículas em face = 1/2 x 6 = 3
Número de partículas na célula 1 + 3 = 4
Cada partícula nesta estrutura está diretamente em contato com 4 outras partículas em sua camada e com 4 partículas na camada acima e 4 partículas na camada abaixo. Assim, o número de coordenação para a estrutura cúbica facetada é 4 + 4 + 4 = 12

Notas:
Para partícula centrada na borda, ela é compartilhada por 4 células unitárias. Assim, cada unidade de célula consiste em 1/4 de partícula O número de átomos por unidade de célula está na mesma proporção que a estequiometria do composto. Portanto, ajuda a prever a fórmula do composto.
Ciência > Química > Estado Sólido > Treliças Bravais