Sistema lineare sottodeterminato
Un sistema sottodeterminato di equazioni lineari ha più incognite che equazioni e generalmente ha un numero infinito di soluzioni. La figura seguente mostra un tale sistema di equazioni y = D x {displaystyle \mathbf {y} =D\mathbf {x} }

dove vogliamo trovare una soluzione per x {displaystyle \mathbf {x} }

.
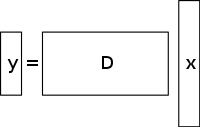
Per scegliere una soluzione di un tale sistema, si devono imporre vincoli o condizioni extra (come la scorrevolezza) come appropriato. Nel rilevamento compresso, si aggiunge il vincolo di sparsità, permettendo solo soluzioni che hanno un piccolo numero di coefficienti non nulli. Non tutti i sistemi sottodeterminati di equazioni lineari hanno una soluzione sparsa. Tuttavia, se c’è un’unica soluzione sparsa al sistema sottodeterminato, allora il quadro di rilevamento compresso permette il recupero di questa soluzione.
Soluzione / metodo di ricostruzione

Il rilevamento compresso sfrutta la ridondanza di molti segnali interessanti – non sono puro rumore. In particolare, molti segnali sono sparsi, cioè contengono molti coefficienti vicini o uguali a zero, quando sono rappresentati in qualche dominio. Questa è la stessa intuizione usata in molte forme di compressione con perdita.
Il rilevamento compresso inizia tipicamente con la presa di una combinazione lineare ponderata di campioni, chiamata anche misurazioni compressive in una base diversa da quella in cui il segnale è noto per essere rado. I risultati trovati da Emmanuel Candès, Justin Romberg, Terence Tao e David Donoho, hanno dimostrato che il numero di queste misure compresse può essere piccolo e contenere ancora quasi tutte le informazioni utili. Pertanto, il compito di riconvertire l’immagine nel dominio previsto comporta la risoluzione di un’equazione di matrice sottodeterminata, poiché il numero di misure compressive prese è inferiore al numero di pixel dell’immagine completa. Tuttavia, l’aggiunta del vincolo che il segnale iniziale è rado permette di risolvere questo sistema sottodeterminato di equazioni lineari.
La soluzione ai minimi quadrati a tali problemi è quella di minimizzare la L 2 {displaystyle L^{2}}

norma, cioè minimizzare la quantità di energia nel sistema. Questo è di solito matematicamente semplice (coinvolgendo solo una moltiplicazione di matrice per la pseudo-inversa della base campionata). Tuttavia, questo porta a risultati scadenti per molte applicazioni pratiche, per le quali i coefficienti sconosciuti hanno energia non nulla.
Per far rispettare il vincolo di sparsità quando si risolve il sistema di equazioni lineari sottodeterminato, si può minimizzare il numero di componenti non nulli della soluzione. La funzione che conta il numero di componenti non nulle di un vettore è stata chiamata L 0 {displaystyle L^{0}}

“norma” di David Donoho.
Candès et al. hanno dimostrato che per molti problemi è probabile che la L 1 {displaystyle L^{1}}

è equivalente alla norma L 0 {displaystyle L^{0}

norma, in senso tecnico: Questo risultato di equivalenza permette di risolvere la norma L 1 {displaystyle L^{1}}

, che è più facile del problema L 0 {displaystyle L^{0}}

problem. Trovare il candidato con il più piccolo L 1 {displaystyle L^{1}}

norma può essere espresso relativamente facilmente come un programma lineare, per il quale esistono già metodi di soluzione efficienti. Quando le misure possono contenere una quantità finita di rumore, il denoising a inseguimento di base è preferito alla programmazione lineare, poiché conserva la sparsità di fronte al rumore e può essere risolto più velocemente di un programma lineare esatto.
Ricostruzione CS basata sulla variazione totale
Motivazione e applicazioni
Ruolo della regolarizzazione TV
La variazione totale può essere vista come un funzionale non negativo a valore reale definito sullo spazio delle funzioni a valore reale (per il caso di funzioni di una variabile) o sullo spazio delle funzioni integrabili (per il caso di funzioni di più variabili). Per i segnali, in particolare, la variazione totale si riferisce all’integrale del gradiente assoluto del segnale. Nella ricostruzione di segnali e immagini, viene applicata come regolarizzazione della variazione totale dove il principio sottostante è che i segnali con dettagli eccessivi hanno un’alta variazione totale e che la rimozione di questi dettagli, pur mantenendo informazioni importanti come i bordi, ridurrebbe la variazione totale del segnale e renderebbe il segnale soggetto più vicino al segnale originale nel problema.
Ai fini della ricostruzione di segnali e immagini, l 1 {\displaystyle l1}

sono utilizzati modelli di minimizzazione. Altri approcci includono anche i minimi quadrati come è stato discusso prima in questo articolo. Questi metodi sono estremamente lenti e restituiscono una ricostruzione non perfetta del segnale. Gli attuali modelli di regolarizzazione CS tentano di affrontare questo problema incorporando priori di sparsità dell’immagine originale, uno dei quali è la variazione totale (TV). Gli approcci TV convenzionali sono progettati per dare soluzioni costanti a metà. Alcuni di questi includono (come discusso in precedenza) – la minimizzazione l1 vincolata che utilizza uno schema iterativo. Questo metodo, anche se veloce, porta in seguito a una lisciatura eccessiva dei bordi con conseguente sfocatura dei bordi dell’immagine. I metodi TV con riponderazione iterativa sono stati implementati per ridurre l’influenza delle grandi grandezze dei valori di gradiente nelle immagini. Questo è stato usato nella ricostruzione della tomografia computerizzata (CT) come metodo noto come variazione totale che preserva i bordi. Tuttavia, poiché le grandezze del gradiente sono utilizzate per la stima dei pesi di penalità relativi tra la fedeltà dei dati e i termini di regolarizzazione, questo metodo non è robusto al rumore e agli artefatti e abbastanza accurato per la ricostruzione dell’immagine/segnale della CS e, quindi, non riesce a preservare le strutture più piccole.
I recenti progressi su questo problema prevedono l’utilizzo di un raffinamento TV direzionale iterativo per la ricostruzione CS. Questo metodo avrebbe 2 fasi: la prima fase stimerebbe e raffinerebbe il campo di orientamento iniziale – che è definito come una stima iniziale point-wise rumorosa, attraverso la rilevazione dei bordi, dell’immagine data. Nella seconda fase, il modello di ricostruzione CS è presentato utilizzando il regolatore TV direzionale. Ulteriori dettagli su questi approcci basati sulla TV – minimizzazione iterativamente ripesata l1, TV che preserva i bordi e modello iterativo che utilizza il campo di orientamento direzionale e la TV – sono forniti di seguito.
Approcci esistenti
Pesata iterativamente l 1 {\displaystyle l_{1}}


minimizzazione

Nei modelli di ricostruzione CS utilizzando l 1 vincolato

minimizzazione, i coefficienti più grandi sono fortemente penalizzati nella l 1 {displaystyle l_{1}}

norm. È stato proposto di avere una formulazione ponderata di l 1 {displaystyle l_{1}}

minimizzazione progettata per penalizzare più democraticamente i coefficienti non nulli. Un algoritmo iterativo è utilizzato per costruire i pesi appropriati. Ogni iterazione richiede la risoluzione di un l 1 {displaystyle l_{1}}

problema di minimizzazione trovando il minimo locale di una funzione di penalità concava che assomiglia di più alla l 0 {displaystyle l_{0}}

norm. Un parametro aggiuntivo, di solito per evitare transizioni brusche nella curva della funzione di penalità, viene introdotto nell’equazione iterativa per garantire la stabilità e in modo che una stima zero in un’iterazione non porti necessariamente a una stima zero nell’iterazione successiva. Il metodo consiste essenzialmente nell’utilizzare la soluzione corrente per calcolare i pesi da utilizzare nell’iterazione successiva.
Avantaggi e svantaggi
Le prime iterazioni possono trovare stime di campione imprecise, tuttavia questo metodo le ridimensiona in una fase successiva per dare più peso alle stime più piccole del segnale non nullo. Uno degli svantaggi è la necessità di definire un punto di partenza valido, poiché un minimo globale potrebbe non essere ottenuto ogni volta a causa della concavità della funzione. Un altro svantaggio è che questo metodo tende a penalizzare uniformemente il gradiente dell’immagine indipendentemente dalle strutture dell’immagine sottostante. Questo provoca una lisciatura eccessiva dei bordi, specialmente quelli delle regioni a basso contrasto, portando successivamente alla perdita di informazioni a basso contrasto. I vantaggi di questo metodo includono: la riduzione della frequenza di campionamento per i segnali sparsi; la ricostruzione dell’immagine mentre è robusta alla rimozione del rumore e di altri artefatti; e l’uso di pochissime iterazioni. Questo può anche aiutare nel recupero di immagini con gradienti sparsi.
Nella figura mostrata sotto, P1 si riferisce al primo passo del processo di ricostruzione iterativa, della matrice di proiezione P della geometria del fascio a ventaglio, che è vincolata dal termine di fedeltà dei dati. Questa può contenere rumore e artefatti poiché non viene eseguita alcuna regolarizzazione. La minimizzazione di P1 è risolta attraverso il metodo dei minimi quadrati a gradiente coniugato. P2 si riferisce al secondo passo del processo di ricostruzione iterativo in cui si utilizza il termine di regolarizzazione della variazione totale che preserva i bordi per rimuovere il rumore e gli artefatti, e quindi migliorare la qualità dell’immagine/segnale ricostruita. La minimizzazione di P2 è fatta attraverso un semplice metodo di discesa del gradiente. La convergenza è determinata testando, dopo ogni iterazione, la positività dell’immagine, controllando se f k – 1 = 0 {\displaystyle f^{k-1}=0}

per il caso in cui f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Si noti che f {displaystyle f}

si riferisce ai diversi coefficienti di attenuazione lineare dei raggi X in diversi voxel dell’immagine del paziente).
La variazione totale (TV) basata sul rilevamento compresso che preserva i bordi

Questo è un algoritmo iterativo di ricostruzione CT con regolarizzazione TV che preserva i bordi per ricostruire immagini CT da dati altamente sottocampionati ottenuti in CT a bassa dose attraverso bassi livelli di corrente (milliampere). Al fine di ridurre la dose di imaging, uno degli approcci utilizzati è quello di ridurre il numero di proiezioni di raggi X acquisite dai rivelatori dello scanner. Tuttavia, questi dati di proiezione insufficienti che vengono utilizzati per ricostruire l’immagine CT possono causare artefatti di striature. Inoltre, l’uso di queste proiezioni insufficienti negli algoritmi TV standard finisce per rendere il problema sottodeterminato e quindi portare a un numero infinito di soluzioni possibili. In questo metodo, una funzione ponderata di penalità aggiuntiva viene assegnata alla norma TV originale. Questo permette di individuare più facilmente le discontinuità di intensità nelle immagini e quindi di adattare il peso per memorizzare le informazioni di bordo recuperate durante il processo di ricostruzione del segnale/immagine. Il parametro σ \displaystyle \sigma }

controlla la quantità di lisciatura applicata ai pixel ai bordi per differenziarli dai pixel non ai bordi. Il valore di σ {displaystyle \sigma }

viene cambiato in modo adattivo in base ai valori dell’istogramma della grandezza del gradiente in modo che una certa percentuale di pixel abbia valori di gradiente maggiori di σ {displaystyle \sigma }

. Il termine di variazione totale che preserva i bordi, quindi, diventa più spartano e questo velocizza l’implementazione. Viene utilizzato un processo di iterazione in due fasi noto come algoritmo di divisione avanti-indietro. Il problema di ottimizzazione è diviso in due sottoproblemi che sono poi risolti rispettivamente con il metodo dei minimi quadrati a gradiente coniugato e il metodo di discesa del gradiente semplice. Il metodo viene fermato quando la convergenza desiderata è stata raggiunta o se viene raggiunto il numero massimo di iterazioni.
Avantaggi e svantaggi
Alcuni degli svantaggi di questo metodo sono l’assenza di strutture più piccole nell’immagine ricostruita e la degradazione della risoluzione dell’immagine. Questo algoritmo TV che preserva i bordi, tuttavia, richiede meno iterazioni dell’algoritmo TV convenzionale. Analizzando i profili d’intensità orizzontali e verticali delle immagini ricostruite, si può vedere che ci sono salti bruschi nei punti di bordo e fluttuazioni trascurabili e minori nei punti non di bordo. Quindi, questo metodo porta a un basso errore relativo e a una maggiore correlazione rispetto al metodo TV. Inoltre, sopprime e rimuove efficacemente qualsiasi forma di rumore dell’immagine e artefatti dell’immagine come le striature.
Modello iterativo usando un campo di orientamento direzionale e una variazione totale direzionale
Per evitare un eccessivo smussamento dei bordi e dei dettagli della trama e per ottenere un’immagine CS ricostruita che sia accurata e robusta al rumore e agli artefatti, viene usato questo metodo. In primo luogo, una stima iniziale del campo di orientamento puntiforme rumoroso dell’immagine I

, d ^ {displaystyle {\hat {d}}}

, si ottiene. Questo campo di orientamento rumoroso è definito in modo che possa essere raffinato in una fase successiva per ridurre le influenze del rumore nella stima del campo di orientamento. Viene quindi introdotta una stima grossolana del campo di orientamento basata sul tensore di struttura che è formulato come: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) {\displaystyle J_{\rho }(\nabla I_{\sigma )=G_{rho }*(\nabla I_{sigma })=(\nabla I_{sigma })={begin{pmatrix}J_{11}&J_{12}J_{12}&J_{22}{end{pmatrix}}}

. Qui, J ρ {displaystyle J_{\rho }}

si riferisce al tensore di struttura relativo al punto pixel dell’immagine (i,j) con deviazione standard ρ {\displaystyle \rho }

. G {displaystyle G}

si riferisce al kernel gaussiano ( 0 , ρ 2 ) {displaystyle (0,\rho ^{2})}

con deviazione standard ρ {displaystyle \rho }

. σ {displaystyle \sigma }

si riferisce al parametro definito manualmente per l’immagine I {\displaystyle I}

al di sotto del quale il rilevamento dei bordi è insensibile al rumore. ∇ I σ {\displaystyle \nabla I_{sigma }}

si riferisce al gradiente dell’immagine I {\displaystyle I}

e ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{sigma})}

si riferisce al prodotto tensoriale ottenuto utilizzando questo gradiente.
Il tensore di struttura ottenuto è convoluto con un kernel gaussiano G {displaystyle G}

per migliorare la precisione della stima dell’orientamento con σ {displaystyle \sigma }

che viene impostato su valori alti per tenere conto dei livelli di rumore sconosciuti. Per ogni pixel (i,j) nell’immagine, il tensore di struttura J è una matrice simmetrica e semi-definita positiva. Convolvendo tutti i pixel dell’immagine con G {displaystyle G}

, dà vettori autoctoni ortonormali ω e υ della J {\displaystyle J}

matrice. ω punta nella direzione dell’orientamento dominante che ha il maggior contrasto e υ punta nella direzione dell’orientamento della struttura che ha il minor contrasto. La stima iniziale grossolana del campo di orientamento d ^ {displaystyle {d}}

è definita come d ^ {displaystyle {\hat {d}}

= υ. Questa stima è accurata ai bordi forti. Tuttavia, ai bordi deboli o su regioni con rumore, la sua affidabilità diminuisce.
Per superare questo inconveniente, viene definito un modello di orientamento raffinato in cui il termine dati riduce l’effetto del rumore e migliora l’accuratezza, mentre il secondo termine di penalità con la norma L2 è un termine di fedeltà che assicura l’accuratezza della stima grossolana iniziale.
Questo campo di orientamento viene introdotto nel modello di ottimizzazione della variazione totale direzionale per la ricostruzione CS attraverso l’equazione m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {displaystyle min_{mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}} \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}
. X {\lPhi \mathrm{X} \rVert _{2}^{2} .

è il segnale obiettivo che deve essere recuperato. Y è il vettore di misura corrispondente, d è il campo di orientamento iterativo raffinato e Φ {displaystyle \Phi }

è la matrice di misurazione CS. Questo metodo subisce alcune iterazioni che alla fine portano alla convergenza. d ^ {displaystyle {\hat {d}}}

è la stima approssimativa del campo di orientamento dell’immagine ricostruita X k – 1 {displaystyle X^{k-1}

dell’iterazione precedente (per controllare la convergenza e le successive prestazioni ottiche, viene usata l’iterazione precedente). Per i due campi vettoriali rappresentati da X {displaystyle \mathrm {X} }

e d {displaystyle d}

, X ∙ d {displaystyle \mathrm {X} \bullet d}

si riferisce alla moltiplicazione dei rispettivi elementi vettoriali orizzontali e verticali di X {\displaystyle \mathrm {X} }

e d {displaystyle d}

seguito dalla loro successiva addizione. Queste equazioni sono ridotte a una serie di problemi di minimizzazione convessi che sono poi risolti con una combinazione di metodi di divisione delle variabili e Lagrangiano aumentato (solutore veloce basato su FFT con una soluzione in forma chiusa). Esso (Lagrangiano aumentato) è considerato equivalente all’iterazione di Bregman spaccata che assicura la convergenza di questo metodo. Il campo di orientamento, d è definito come uguale a ( d h , d v ) {displaystyle (d_{h},d_{v})}

, dove d h , d v {displaystyle d_{h},d_{v}}

definiscono le stime orizzontali e verticali di d {displaystyle d}

.

Il metodo lagrangiano aumentato per il campo di orientamento, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {displaystyle min_{mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{frac {\lambda }{2}} \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}
, comporta l’inizializzazione di d h, d v, H, V {displaystyle d_{h},d_{v},H,V}

e poi trovare il minimizzatore approssimato di L 1 {\displaystyle L_{1}}

rispetto a queste variabili. I moltiplicatori lagrangiani vengono poi aggiornati e il processo iterativo viene fermato quando si raggiunge la convergenza. Per il modello iterativo di raffinamento della variazione totale, il metodo lagrangiano aumentato comporta l’inizializzazione di X, P, Q, λ P, λ Q {displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}

.
Qui, H , V , P , Q {\displaystyle H,V,P,Q}

sono variabili di nuova introduzione dove H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}

, V {displaystyle V}

= ∇ d v {displaystyle \nabla d_{v}

, P {\displaystyle P}

= ∇ X {displaystyle \nabla \mathrm {X} }

, e Q {displaystyle Q}

= P ∙ d {displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}
sono i moltiplicatori lagrangiani per H , V , P , Q {\displaystyle H,V,P,Q}

. Per ogni iterazione, il minimizzatore approssimato di L 2 {\displaystyle L_{2}

rispetto alle variabili ( X , P , Q {displaystyle \mathrm {X} ,P,Q}

) è calcolato. E come nel modello di raffinamento del campo, i moltiplicatori lagrangiani vengono aggiornati e il processo iterativo si ferma quando si raggiunge la convergenza.
Per il modello di affinamento del campo di orientamento, i moltiplicatori lagrangiani vengono aggiornati nel processo iterativo come segue:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Per il modello iterativo di affinamento della variazione totale direzionale, i moltiplicatori di Lagrangian sono aggiornati come segue:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}bullet d)}

qui, γ H , γ V , γ P , γ Q {displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

sono costanti positive.
Svantaggi e svantaggi
Basandosi sul rapporto segnale-rumore di picco (PSNR) e sull’indice di somiglianza strutturale (SSIM) e su immagini di verità note per testare le prestazioni, si conclude che la variazione totale direzionale iterativa ha una migliore prestazione di ricostruzione rispetto ai metodi non iterativi nel preservare le aree dei bordi e delle texture. Il modello di affinamento del campo di orientamento gioca un ruolo importante in questo miglioramento delle prestazioni, poiché aumenta il numero di pixel senza direzione nell’area piatta, mentre migliora la coerenza del campo di orientamento nelle regioni con bordi.