Un automat celular este o colecție de celule „colorate” pe o grilă de formă specificată care evoluează printr-un număr de pași discreți în timp conform unui set de reguli bazate pe stările celulelor învecinate. Regulile sunt apoi aplicate iterativ pentru atâția pași de timp câți pași de timp se doresc. von Neumann a fost unul dintre primii oameni care au luat în considerare un astfel de model și a încorporat un model celular în „constructorul său universal”. Automatele celulare au fost studiate la începutul anilor 1950 ca un posibil model pentru sistemele biologice (Wolfram 2002, p. 48). Studii cuprinzătoare ale automatelor celulare au fost efectuate de S. Wolfram începând cu anii 1980, iar cercetările fundamentale ale lui Wolfram în acest domeniu au culminat cu publicarea cărții sale A New Kind of Science (Wolfram 2002), în care Wolfram prezintă o colecție gigantică de rezultate referitoare la automate, printre care se numără o serie de noi descoperiri revoluționare.
Episodul din sezonul 2 „Bettor or Worse” (2006) al serialului polițist de televiziune NUMB3RS menționează automatele celulare unidimensionale.
Automatele celulare vin într-o varietate de forme și varietăți. Una dintre cele mai fundamentale proprietăți ale unui automat celular este tipul de grilă pe care este calculat. Cea mai simplă astfel de „grilă” este o linie unidimensională. În două dimensiuni, pot fi luate în considerare grilele pătrate, triunghiulare și hexagonale. Automatele celulare pot fi, de asemenea, construite pe grile carteziene într-un număr arbitrar de dimensiuni, rețeaua 
dimensională de numere întregi 
fiind cea mai frecventă alegere. Automatele celulare pe o rețea de numere întregi 
-dimensionale sunt implementate în limbajul Wolfram sub numele de CellularAutomaton.
Numărul de culori (sau stări distincte) 
pe care le poate lua un automat celular trebuie, de asemenea, specificat. Acest număr este de obicei un număr întreg, 
(binar) fiind cea mai simplă alegere. Pentru un automat binar, culoarea 0 este denumită în mod obișnuit „alb”, iar culoarea 1 este denumită în mod obișnuit „negru”. Cu toate acestea, pot fi luate în considerare și automatele celulare care au o gamă continuă de valori posibile.
În plus față de grila pe care trăiește un automat celular și de culorile pe care le pot lua celulele sale, trebuie specificată și vecinătatea peste care celulele se afectează reciproc. Cea mai simplă alegere este „vecinii cei mai apropiați”, în care numai celulele direct adiacente unei anumite celule pot fi afectate la fiecare pas de timp. Două vecinătăți comune în cazul unui automat celular bidimensional pe o grilă pătrată sunt așa-numitul cartier Moore (un cartier pătrat) și cartierul von Neumann (un cartier în formă de romb).
Cel mai simplu tip de automat celular este un automat binar, cel mai apropiat de vecini, unidimensional. Astfel de automate au fost numite „automate celulare elementare” de către S. Wolfram, care a studiat pe larg proprietățile lor uimitoare (Wolfram 1983; 2002, p. 57). Există 256 de astfel de automate, fiecare dintre acestea putând fi indexat cu un număr binar unic a cărui reprezentare zecimală este cunoscută sub numele de „regulă” pentru automatul respectiv. O ilustrare a regulii 30 este prezentată mai sus, împreună cu evoluția pe care o produce după 15 pași pornind de la o singură celulă neagră.
O clasă ceva mai complicată de automate celulare sunt automatele celulare totaliste unidimensionale cu cel mai apropiat vecin, 
culori, cu o singură dimensiune. În astfel de automate, media celulelor adiacente este cea care determină evoluția, iar cele mai simple exemple netriviale au 
culori. Pentru aceste automate, setul de reguli care descriu comportamentul poate fi codificat sub forma unui număr 
de 
cifre, cunoscut sub numele de „cod”. Regulile și cei 300 de pași ai automatului ternar (
) cod 912 sunt ilustrate mai sus.
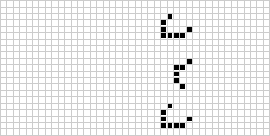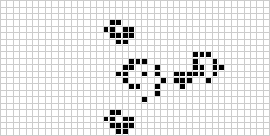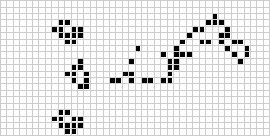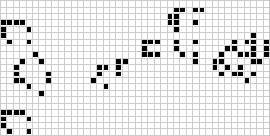
În două dimensiuni, cel mai cunoscut automat celular este jocul vieții al lui Conway, descoperit de J. H. Conway în 1970 și popularizat în rubricile lui Martin Gardner din Scientific American. Jocul vieții este un automat celular totalist binar (
) cu o vecinătate Moore de domeniul 
. Deși calcularea generațiilor succesive ale jocului vieții s-a făcut inițial manual, revoluția informatică a sosit curând și a permis studierea și propagarea unor modele mai extinse. O animație a construcției jocului vieții cunoscută sub numele de trenul puffer este ilustrată mai sus.
WireWorld este un alt automat celular bidimensional comun.
Teoria automatelor celulare este extrem de bogată, reguli și structuri simple fiind capabile să producă o mare varietate de comportamente neașteptate. De exemplu, există automate celulare universale care sunt capabile să simuleze comportamentul oricărui alt automat celular sau mașină Turing. A fost chiar demonstrat de Gacs (2001) că există automate celulare universale tolerante la erori, a căror capacitate de a simula alte automate celulare nu este împiedicată de perturbații aleatorii, cu condiția ca aceste perturbații să fie suficient de rarefiate.
.