Biografie

Brahmagupta (598-668 d.Hr.)
Marele matematician și astronom indian din secolul al VII-lea Brahmagupta a scris câteva lucrări importante atât în domeniul matematicii, cât și al astronomiei. Era originar din statul Rajasthan din nord-vestul Indiei (este adesea denumit Bhillamalacarya, profesorul din Bhillamala), iar mai târziu a devenit șeful observatorului astronomic din Ujjain, în centrul Indiei. Majoritatea lucrărilor sale sunt compuse în versuri eliptice, o practică obișnuită în matematica indiană la acea vreme, și, prin urmare, au o oarecare notă poetică.
Se pare că este probabil ca lucrările lui Brahmagupta, în special cel mai faimos text al său, „Brahmasphutasiddhanta”, să fi fost aduse de către califul abbasid Al-Mansur din secolul al VIII-lea în centrul său de învățare nou înființat la Bagdad, pe malurile Tigrului, oferind o legătură importantă între matematica și astronomia indiană și emergența în curs de dezvoltare a științei și matematicii în lumea islamică.
În lucrarea sa despre aritmetică, Brahmagupta a explicat cum să găsească cubul și rădăcina cubică a unui număr întreg și a dat reguli care să faciliteze calculul pătratelor și al rădăcinilor pătrate. El a dat, de asemenea, reguli pentru tratarea a cinci tipuri de combinații de fracții. El a dat suma pătratelor primelor n numere naturale ca fiind n(n + 1)(2n + 1)⁄ 6 și suma cuburilor primelor n numere naturale ca fiind (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Tratează zero ca pe un număr

Reguli ale lui Brahmagupta pentru tratarea numerelor zero și a numerelor negative
Geniul lui Brahmagupta, însă, a venit în tratarea conceptului (pe atunci relativ nou) de număr zero. Deși este adesea atribuit și matematicianului indian din secolul al VII-lea Bhaskara I, „Brahmasphutasiddhanta” a sa este probabil cel mai vechi text cunoscut care tratează zero ca număr de sine stătător, mai degrabă decât ca o simplă cifră de rezervă, așa cum făceau babilonienii, sau ca simbol al lipsei de cantitate, așa cum făceau grecii și romanii.
Brahmagupta a stabilit regulile matematice de bază pentru tratarea lui zero (1 + 0 = 1; 1 – 0 = 1; și 1 x 0 = 0), deși înțelegerea sa privind împărțirea la zero era incompletă (el credea că 1 ÷ 0 = 0). Aproape 500 de ani mai târziu, în secolul al XII-lea, un alt matematician indian, Bhaskara al II-lea, a arătat că răspunsul ar trebui să fie infinitul, nu zero (pe motiv că 1 poate fi împărțit într-un număr infinit de bucăți de mărimea zero), un răspuns care a fost considerat corect timp de secole. Cu toate acestea, această logică nu explică de ce 2 ÷ 0, 7 ÷ 0 etc. ar trebui să fie, de asemenea, zero – punctul de vedere modern este că un număr împărțit la zero este de fapt „nedefinit” (adică nu are sens).
Viziunea lui Brahmagupta asupra numerelor ca entități abstracte, mai degrabă decât doar pentru numărare și măsurare, i-a permis să facă încă un salt conceptual uriaș, care va avea consecințe profunde pentru matematica viitoare. Anterior, suma 3 – 4, de exemplu, era considerată fie lipsită de sens, fie, în cel mai bun caz, doar zero. Cu toate acestea, Brahmagupta și-a dat seama că ar putea exista un astfel de număr negativ, pe care l-a numit „datorie”, spre deosebire de „proprietate”. El a expus regulile de tratare a numerelor negative (de exemplu, un negativ înmulțit cu un negativ este un pozitiv, un negativ înmulțit cu un pozitiv este un negativ etc.).
În plus, a subliniat el, ecuațiile pătratice (de tipul x2 + 2 = 11, de exemplu) ar putea avea, în teorie, două soluții posibile, dintre care una ar putea fi negativă, pentru că 32 = 9 și -32 = 9. Pe lângă lucrările sale privind soluțiile ecuațiilor liniare generale și ale ecuațiilor pătratice, Brahmagupta a mers și mai departe, luând în considerare sistemele de ecuații simultane (set de ecuații care conțin mai multe variabile) și rezolvând ecuații pătratice cu două necunoscute, lucru care nu a fost luat în considerare în Occident decât o mie de ani mai târziu, când Fermat a luat în considerare probleme similare în 1657.
Teorema lui Brahmagupta despre cvadrilateralele ciclice
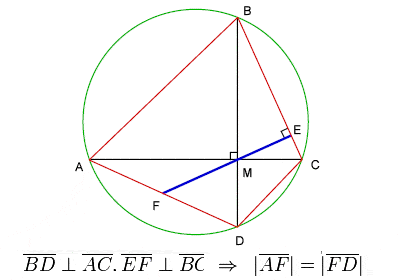
Teorema lui Brahmagupta despre cvadrilateralele ciclice
Brahmagupta a încercat chiar să scrie aceste concepte destul de abstracte, folosind inițialele numelor culorilor pentru a reprezenta necunoscutele din ecuațiile sale, una dintre primele indicii a ceea ce cunoaștem astăzi ca algebră.
Brahmagupta a dedicat o parte substanțială a operei sale geometriei și trigonometriei. El a stabilit √10 (3,162277) ca fiind o bună aproximație practică pentru π (3,141593) și a dat o formulă, cunoscută acum sub numele de Formula lui Brahmagupta, pentru aria unui cvadrilateriu ciclic, precum și o teoremă celebră privind diagonalele unui cvadrilateriu ciclic, denumită de obicei Teorema lui Brahmagupta.
| << Înapoi la Matematică indiană | Înapoi la Madhava >> |
.