Coordonate baricentrice

de
Geometrie > CoordonateGeometry >
Geometrie > Geometrie plană > Triunghiuri > Proprietăți ale triunghiurilor >

Coordonatele baricentrice sunt triplete de numere (t_1,t_2,t_3) care corespund unor mase plasate la vârfurile unui triunghi de referință DeltaA_1A_2A_3. Aceste mase determină apoi un punct P, care este centroidul geometric al celor trei mase și care este identificat cu coordonatele (t_1,t_2,t_3). Vârfurile triunghiului sunt date de (1,0,0), (0,1,0) și (0,0,1). Coordonatele baricentrice au fost descoperite de Möbius în 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).

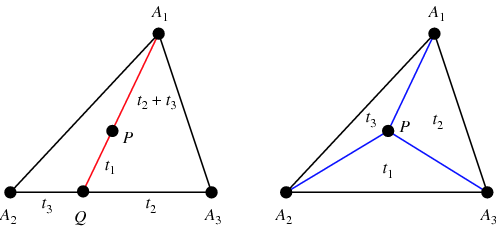
Barycentric

Pentru a afla coordonatele baricentrice pentru un punct arbitrar P, găsiți t_2 și t_3 din punctul Q aflat la intersecția dreptei A_1P cu latura A_2A_3, și apoi determinați t_1 ca fiind masa de la A_1 care va echilibra o masă t_2+t_3 la Q, făcând astfel ca P să fie centroidul (figura din stânga). În plus, ariile triunghiurilor DeltaA_1A_2P, DeltaA_1A_3P și DeltaA_2A_3P sunt proporționale cu coordonatele baricentrice t_3, t_2 și t_1 ale lui P (figura din dreapta; Coxeter 1969, p. 217).

Coordonatele baricentrice sunt omogene, deci

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

pentru mu!=0.

Coordonatele baricentrice normalizate astfel încât să devină ariile reale ale subtriunghiurilor se numesc coordonate baricentrice omogene. Coordonatele baricentrice normalizate astfel încât

t_1+t_2+t_3=1,
(2)

pentru ca coordonatele să dea ariile subtriunghiurilor normalizate în funcție de aria triunghiului inițial se numesc coordonate areale (Coxeter 1969, p. 218). Coordonatele baricentrice și areale pot furniza demonstrații deosebit de elegante ale unor teoreme geometrice, cum ar fi teorema lui Routh, teorema lui Ceva și teorema lui Menelaus (Coxeter 1969, pp. 219-221).

Coordonatele baricentrice (nu neapărat omogene) pentru un număr de centre comune sunt rezumate în tabelul următor. În tabel, a, b și c sunt lungimile laturilor triunghiului, iar s este semiperimetrul acestuia.

centrul triunghiului coordonate baricentrice
circumcentrul O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
Punctul Gergonne Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incentru I (a,b,c)
Punctul Nagel Na (s-a,s-b,s-c)
ortocentrul H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
punct simedian K (a^2,b^2,c^2)
centroidul triunghiului G (1,1,1)

În coordonate baricentrice, o dreaptă are o ecuație liniară omogenă. În particular, dreapta care unește punctele (r_1,r_2,r_3) și (s_1,s_2,s_3) are ecuația

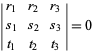|r_1 r_2 r_3; s_1 s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 și 57; Coxeter 1969, p. 219; Bottema 1982). Dacă vârfurile P_i ale unui triunghi DeltaP_1P_2P_3 au coordonatele baricentrice (x_i,y_i,z_i), atunci aria triunghiului este

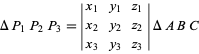DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Lasă un comentariu