Sistem liniar subdeterminat
Un sistem subdeterminat de ecuații liniare are mai multe necunoscute decât ecuații și, în general, are un număr infinit de soluții. Figura de mai jos prezintă un astfel de sistem de ecuații y = D x {\displaystyle \mathbf {y} =D\mathbf {x}. }

unde dorim să găsim o soluție pentru x {\displaystyle \mathbf {x} }

.
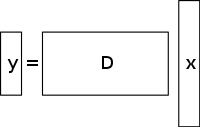
Pentru a alege o soluție la un astfel de sistem, trebuie să se impună constrângeri sau condiții suplimentare (cum ar fi netezimea), după caz. În detecția comprimată, se adaugă constrângerea de dispersie, permițând numai soluțiile care au un număr mic de coeficienți nenule. Nu toate sistemele subdeterminate de ecuații liniare au o soluție rarefiată. Cu toate acestea, în cazul în care există o soluție unică rarefiată pentru sistemul subdeterminat, atunci cadrul de detecție comprimată permite recuperarea acelei soluții.
Soluție / metodă de reconstrucție

Senzația comprimată profită de redundanța din multe semnale interesante – acestea nu sunt zgomot pur. În special, multe semnale sunt rarefiate, adică ele conțin mulți coeficienți apropiați sau egali cu zero, atunci când sunt reprezentate într-un anumit domeniu. Aceasta este aceeași intuiție utilizată în multe forme de compresie cu pierderi.
Senzația comprimată începe de obicei cu luarea unei combinații liniare ponderate de eșantioane numite și măsurători compresive într-o bază diferită de baza în care se știe că semnalul este rarefiat. Rezultatele găsite de Emmanuel Candès, Justin Romberg, Terence Tao și David Donoho, au arătat că numărul acestor măsurători compresive poate fi mic și totuși să conțină aproape toate informațiile utile. Prin urmare, sarcina de a converti imaginea înapoi în domeniul vizat implică rezolvarea unei ecuații matriceale subdeterminate, deoarece numărul de măsurători compresive efectuate este mai mic decât numărul de pixeli din imaginea completă. Cu toate acestea, adăugarea constrângerii ca semnalul inițial să fie rarefiat permite rezolvarea acestui sistem subdeterminat de ecuații liniare.
Soluția celor mai mici pătrate pentru astfel de probleme este de a minimiza L 2 {\displaystyle L^{2}}

normă – adică minimizarea cantității de energie din sistem. Acest lucru este, de obicei, simplu din punct de vedere matematic (implicând doar o înmulțire a matricei cu pseudo-inversul bazei eșantionate în). Cu toate acestea, acest lucru conduce la rezultate slabe pentru multe aplicații practice, pentru care coeficienții necunoscuți au energie diferită de zero.
Pentru a impune constrângerea de zgârcenie atunci când se rezolvă sistemul subdeterminat de ecuații liniare, se poate minimiza numărul de componente non-zero ale soluției. Funcția care numără numărul de componente non-zero ale unui vector a fost numită L 0 {\displaystyle L^{0}}.

„normă” de către David Donoho.
Candès et al. au demonstrat că pentru multe probleme este probabil ca norma L 1 {\displaystyle L^{1}}

este echivalentă cu norma L 0 {\displaystyle L^{0}}.

normă, într-un sens tehnic: Acest rezultat de echivalență permite rezolvarea normei L 1 {\displaystyle L^{1}}.

problemă, care este mai ușoară decât L 0 {\displaystyle L^{0}}.

problem. Găsirea candidatului cu cel mai mic L 1 {\displaystyle L^{1}}.

normă poate fi exprimată relativ ușor sub forma unui program liniar, pentru care există deja metode eficiente de rezolvare. În cazul în care măsurătorile pot conține o cantitate finită de zgomot, denotarea prin urmărirea bazei este preferată în locul programării liniare, deoarece conservă sparsitatea în fața zgomotului și poate fi rezolvată mai rapid decât un program liniar exact.
Reconstrucția CS pe bază de variație totală
Motivație și aplicații
Rolul regularizării TV
Variația totală poate fi văzută ca o funcțională cu valori reale non-negative definită pe spațiul funcțiilor cu valori reale (pentru cazul funcțiilor de o variabilă) sau pe spațiul funcțiilor integrabile (pentru cazul funcțiilor de mai multe variabile). Pentru semnale, în special, variația totală se referă la integrala gradientului absolut al semnalului. În reconstrucția semnalelor și a imaginilor, se aplică ca regularizare a variației totale, unde principiul de bază este că semnalele cu detalii excesive au o variație totală mare și că eliminarea acestor detalii, păstrând în același timp informații importante, cum ar fi marginile, ar reduce variația totală a semnalului și ar face ca subiectul semnalului să fie mai aproape de semnalul original din problemă.
În scopul reconstrucției semnalelor și a imaginilor, l 1 {\displaystyle l1}

se utilizează modele de minimizare. Alte abordări includ, de asemenea, metoda celor mai mici pătrate, așa cum a fost discutat anterior în acest articol. Aceste metode sunt extrem de lente și returnează o reconstrucție nu foarte perfectă a semnalului. Modelele actuale de regularizare CS încearcă să abordeze această problemă prin încorporarea unor priorități de dispersie a imaginii originale, dintre care una este variația totală (TV). Abordările TV convenționale sunt concepute pentru a oferi soluții constante la bucată. Unele dintre acestea includ (după cum se discută mai departe) – limitarea l1-minimizare care utilizează o schemă iterativă. Această metodă, deși este rapidă, duce ulterior la o supradimensionare a marginilor, ceea ce duce la o imagine neclară. Metodele TV cu reponderare iterativă au fost implementate pentru a reduce influența magnitudinilor mari ale valorilor de gradient din imagini. Această metodă a fost utilizată în reconstrucția tomografiei computerizate (CT) sub forma unei metode cunoscute sub numele de variație totală de conservare a marginilor. Cu toate acestea, deoarece mărimile gradientului sunt utilizate pentru estimarea ponderilor relative de penalizare între fidelitatea datelor și termenii de regularizare, această metodă nu este robustă la zgomot și artefacte și nu este suficient de precisă pentru reconstrucția imaginii/semnalului CS și, prin urmare, nu reușește să păstreze structurile mai mici.
Progrese recente în această problemă implică utilizarea unui rafinament TV direcțional iterativ pentru reconstrucția CS. Această metodă ar avea 2 etape: prima etapă ar estima și rafina câmpul de orientare inițial – care este definit ca o estimare inițială punctuală zgomotoasă, prin detectarea marginilor, a imaginii date. În a doua etapă, modelul de reconstrucție CS este prezentat prin utilizarea regularizatorului TV direcțional. Mai multe detalii despre aceste abordări bazate pe TV – minimizarea l1 reponderată iterativ, TV cu prezervarea marginilor și modelul iterativ care utilizează câmpul de orientare direcțional și TV – sunt furnizate mai jos.
Abordări existente
Iteratively reweighted l 1 {\displaystyle l_{1}}


minimizare

În modelele de reconstrucție CS care utilizează l 1 constrâns {\displaystyle l_{1}}.

minimizare, coeficienții mai mari sunt puternic penalizați în l 1 {\displaystyle l_{1}}.

norm. S-a propus o formulare ponderată a l 1 {\displaystyle l_{1}}.

minimizare concepută pentru a penaliza mai democratic coeficienții care nu sunt zero. Se utilizează un algoritm iterativ pentru construirea ponderilor adecvate. Fiecare iterație necesită rezolvarea unui l 1 {\displaystyle l_{1}}.

problemă de minimizare prin găsirea minimului local al unei funcții de penalizare concave care seamănă mai mult cu l 0 {\displaystyle l_{0}}.

norm. În ecuația iterativă se introduce un parametru suplimentar, de obicei pentru a evita orice tranziție bruscă în curba funcției de penalizare, pentru a asigura stabilitatea și pentru ca o estimare zero într-o iterație să nu ducă neapărat la o estimare zero în iterația următoare. Metoda implică, în esență, utilizarea soluției curente pentru calcularea ponderilor care urmează să fie utilizate în iterația următoare.
Avantaje și dezavantaje
În iterațiile timpurii se pot găsi estimări de eșantionare inexacte, însă această metodă le va eșantiona mai puțin într-o etapă ulterioară pentru a da mai multă greutate estimărilor mai mici ale semnalelor care nu sunt zero. Unul dintre dezavantaje este necesitatea de a defini un punct de pornire valid, deoarece este posibil ca un minim global să nu fie obținut de fiecare dată din cauza concavității funcției. Un alt dezavantaj este că această metodă tinde să penalizeze uniform gradientul imaginii, indiferent de structurile imaginii subiacente. Acest lucru determină o supraslăbire a marginilor, în special a celor din regiunile cu contrast scăzut, ceea ce duce ulterior la pierderea informațiilor cu contrast scăzut. Printre avantajele acestei metode se numără: reducerea ratei de eșantionare pentru semnalele rare; reconstrucția imaginii, fiind în același timp robustă la eliminarea zgomotului și a altor artefacte; și utilizarea unui număr foarte mic de iterații. Aceasta poate ajuta, de asemenea, la recuperarea imaginilor cu gradienți rari.
În figura de mai jos, P1 se referă la prima etapă a procesului de reconstrucție iterativă, a matricei de proiecție P a geometriei fasciculului în evantai, care este constrânsă de termenul de fidelitate a datelor. Aceasta poate conține zgomot și artefacte, deoarece nu se efectuează nicio regularizare. Minimizarea lui P1 se rezolvă prin metoda celor mai mici pătrate cu gradient conjugat. P2 se referă la a doua etapă a procesului iterativ de reconstrucție, în care se utilizează termenul de regularizare a variației totale de păstrare a marginilor pentru a elimina zgomotul și artefactele și, astfel, pentru a îmbunătăți calitatea imaginii/semnalului reconstruit. Minimizarea lui P2 se realizează printr-o metodă simplă de coborâre a gradientului. Convergența este determinată prin testarea, după fiecare iterație, a pozitivității imaginii, prin verificarea dacă f k – 1 = 0 {\displaystyle f^{k-1}=0}.

pentru cazul în care f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Observați că f {\displaystyle f}

se referă la diferiți coeficienți de atenuare liniară a razelor X la diferiți voxeli din imaginea pacientului).
Detecție comprimată bazată pe variația totală (TV) cu prezervarea marginilor

Acesta este un algoritm iterativ de reconstrucție CT cu regularizare TV cu prezervarea marginilor pentru a reconstrui imagini CT din date cu subeșantionare mare obținute la CT cu doză mică prin niveluri scăzute de curent (miliamperi). Pentru a reduce doza de imagistică, una dintre abordările utilizate constă în reducerea numărului de proiecții de raze X achiziționate de detectoarele scanerului. Cu toate acestea, aceste date de proiecție insuficiente care sunt utilizate pentru a reconstrui imaginea CT pot cauza artefacte de tip streaking. În plus, utilizarea acestor proiecții insuficiente în algoritmii standard de televiziune sfârșește prin a face ca problema să fie subdeterminată și, astfel, să conducă la un număr infinit de soluții posibile. În această metodă, o funcție suplimentară de penalizare ponderată este atribuită normei TV originale. Acest lucru permite o detectare mai ușoară a discontinuităților bruște de intensitate în imagini și, astfel, adaptarea ponderii pentru a stoca informațiile de margine recuperate în timpul procesului de reconstrucție a semnalului/imaginii. Parametrul σ {\displaystyle \sigma }

controlează gradul de netezire aplicat pixelilor de la margini pentru a-i diferenția de pixelii fără margini. Valoarea lui σ {\displaystyle \sigma }

este modificată în mod adaptiv pe baza valorilor histogramei magnitudinii gradientului, astfel încât un anumit procent de pixeli să aibă valori ale gradientului mai mari decât σ {\displaystyle \sigma }

. Astfel, termenul de variație totală care păstrează marginile devine mai rarefiat, ceea ce accelerează implementarea. Se utilizează un proces de iterație în doi pași cunoscut sub numele de algoritmul de divizare înainte-înapoi. Problema de optimizare este împărțită în două subprobleme care sunt apoi rezolvate cu metoda celor mai mici pătrate cu gradient conjugat și, respectiv, cu metoda simplă de coborâre a gradientului. Metoda este oprită atunci când se obține convergența dorită sau dacă se atinge numărul maxim de iterații.
Avantaje și dezavantaje
Câteva dintre dezavantajele acestei metode sunt absența structurilor mai mici în imaginea reconstruită și degradarea rezoluției imaginii. Cu toate acestea, acest algoritm TV de păstrare a marginilor necesită mai puține iterații decât algoritmul TV convențional. Analizând profilurile de intensitate orizontală și verticală ale imaginilor reconstruite, se poate observa că există salturi bruște în punctele de margine și fluctuații neglijabile, minore, în punctele fără margini. Astfel, această metodă conduce la o eroare relativă scăzută și la o corelație mai mare în comparație cu metoda TV. De asemenea, suprimă și elimină în mod eficient orice formă de zgomot de imagine și artefacte de imagine, cum ar fi striațiile.
Model iterativ care utilizează un câmp de orientare direcțională și o variație totală direcțională
Pentru a preveni supradimensionarea marginilor și a detaliilor de textură și pentru a obține o imagine CS reconstruită care este precisă și rezistentă la zgomot și artefacte, se utilizează această metodă. Mai întâi, se realizează o estimare inițială a câmpului de orientare punctuală zgomotoasă a imaginii I {\displaystyle I}.

, d ^ { {\displaystyle {\hat {d}}}}

, se obține. Acest câmp de orientare zgomotos este definit astfel încât să poată fi rafinat într-o etapă ulterioară pentru a reduce influențele zgomotului în estimarea câmpului de orientare. Se introduce apoi o estimare grosieră a câmpului de orientare pe baza tensorului de structură, care se formulează astfel: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 12 J 22 ) {\displaystyle J_{\rho }(\nabla I_{\sigma })=G_{\rho }*(\nabla I_{\sigma }\otimes \nabla I_{\sigma })={\begin{pmatrix}J_{11}&J_{12}\\\\J_{12}&J_{22}\end{pmatrix}}}}

. Aici, J ρ {\displaystyle J_{\rho }}

se referă la tensorul de structură legat de punctul de pixel al imaginii (i,j) având deviația standard ρ {\displaystyle \rho }

. G {\displaystyle G}

se referă la nucleul gaussian ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

cu deviația standard ρ {\displaystyle \rho }

. σ {\displaystyle \sigma }

se referă la parametrul definit manual pentru imaginea I {\displaystyle I}

sub care detectarea marginilor este insensibilă la zgomot. ∇ I σ {\displaystyle \nabla I_{\sigma }}}.

se referă la gradientul imaginii I {\displaystyle I}.

și ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{\sigma }\otimes \nabla I_{\sigma })}

se referă la produsul tensorial obținut prin utilizarea acestui gradient.
Tensorul de structură obținut se convolează cu un nucleu gaussian G {\displaystyle G}

pentru a îmbunătăți precizia estimării orientării cu σ {\displaystyle \sigma }

fiind setat la valori ridicate pentru a ține seama de nivelurile de zgomot necunoscute. Pentru fiecare pixel (i,j) din imagine, tensorul de structură J este o matrice simetrică și semi-definită pozitivă. Convoluția tuturor pixelilor din imagine cu G {\displaystyle G}.

, se obțin vectorii proprii ortonormali ω și υ ai lui J {\displaystyle J}.

matrice. ω punctează în direcția orientării dominante care are cel mai mare contrast, iar υ punctează în direcția orientării structurii care are cel mai mic contrast. Estimarea inițială grosieră a câmpului de orientare d ^ {\displaystyle {\hat {d}}}}.

se definește ca d ^ {\displaystyle {\hat {d}}}.

= υ. Această estimare este precisă în cazul marginilor puternice. Cu toate acestea, la marginile slabe sau în regiunile cu zgomot, fiabilitatea sa scade.
Pentru a depăși acest dezavantaj, se definește un model de orientare rafinat în care termenul de date reduce efectul zgomotului și îmbunătățește acuratețea, în timp ce al doilea termen de penalizare cu norma L2 este un termen de fidelitate care asigură acuratețea estimării grosiere inițiale.
Acest câmp de orientare este introdus în modelul de optimizare a variației totale direcționale pentru reconstrucția CS prin intermediul ecuației: m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}.

. X {\displaystyle \mathrm {X} }

este semnalul obiectiv care trebuie recuperat. Y este vectorul de măsurare corespunzător, d este câmpul de orientare rafinat iterativ și Φ {\displaystyle \Phi }

este matricea de măsurare CS. Această metodă trece prin câteva iterații care conduc în cele din urmă la convergență. d ^ {\displaystyle {\hat {d}}}}

este estimarea aproximativă a câmpului de orientare a imaginii reconstruite X k – 1 {\displaystyle X^{k-1}}.

din iterația anterioară (pentru a verifica convergența și performanța optică ulterioară, se utilizează iterația anterioară). Pentru cele două câmpuri vectoriale reprezentate de X {\displaystyle \mathrm {X} }

și d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm {X} \bullet d}

se referă la înmulțirea elementelor vectoriale orizontale și verticale respective ale lui X {\displaystyle \mathrm {X} }

și d {\displaystyle d}

urmată de adăugarea lor ulterioară. Aceste ecuații sunt reduse la o serie de probleme de minimizare convexă care sunt apoi rezolvate cu o combinație de metode de divizare a variabilelor și Lagrangian augmentat (rezolvare rapidă bazată pe FFT cu o soluție în formă închisă). Aceasta (Augmented Lagrangian) este considerată echivalentă cu iterația Bregman divizată care asigură convergența acestei metode. Câmpul de orientare d este definit ca fiind egal cu ( d h , d v ) {\displaystyle (d_{h},d_{v})}.

, unde d h , d v {\displaystyle d_{h},d_{v}} {\displaystyle d_{h},d_{v}}

definesc estimările orizontale și verticale ale lui d {\displaystyle d}

.

Metoda Lagrangiană augmentată pentru câmpul de orientare, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}.

, presupune inițializarea d h , d v , H , V {\displaystyle d_{h},d_{v},H,V}

și apoi găsirea minimizatorului aproximat al lui L 1 {\displaystyle L_{1}}

cu privire la aceste variabile. Multiplicatorii lui Lagrange sunt apoi actualizați, iar procesul iterativ este oprit atunci când se atinge convergența. Pentru modelul iterativ de rafinare a variației totale direcționale, metoda lagrangiană augmentată implică inițializarea X , P , Q , λ P , λ Q {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}.

.
Aici, H , V , P , Q {\displaystyle H,V,P,Q}

sunt variabile nou introduse unde H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}}

, V {\displaystyle V}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {\displaystyle P}

= ∇ X {\displaystyle \nabla \mathrm {X} }

, și Q {\displaystyle Q}

= P ∙ d {\displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}}

sunt multiplicatorii Lagrangian pentru H , V , P , Q {\displaystyle H,V,P,Q}

. Pentru fiecare iterație, minimizatorul aproximat al lui L 2 {\displaystyle L_{2}}.

în ceea ce privește variabilele ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}

) se calculează. Și la fel ca în modelul de rafinare a câmpului, multiplicatorii lagrangianului sunt actualizați, iar procesul iterativ este oprit atunci când se atinge convergența.
Pentru modelul de rafinare a câmpului de orientare, multiplicatorii lagrangiani sunt actualizați în procesul iterativ după cum urmează:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Pentru modelul iterativ de rafinare a variației totale direcționale, multiplicatorii Lagrangian sunt actualizați după cum urmează:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}

Aici, γ H , γ V , γ P , γ Q {\displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

sunt constante pozitive.
Vantaje și dezavantaje
Pe baza indicilor de măsurare a raportului semnal/zgomot maxim (PSNR) și a indicelui de similaritate structurală (SSIM) și a imaginilor de referință cunoscute pentru testarea performanțelor, se concluzionează că variația totală direcțională iterativă are o performanță de reconstrucție mai bună decât metodele neiterative în ceea ce privește conservarea zonelor de margine și textură. Modelul de rafinare a câmpului de orientare joacă un rol major în această îmbunătățire a performanței, deoarece crește numărul de pixeli fără direcție în zona plană, îmbunătățind în același timp consistența câmpului de orientare în regiunile cu muchii.
.