Factorul de compresibilitate (gaze) - Knowino

De la Knowino

Aceasta este o versiune verificată a acestei pagini

Salt la: navigation,search

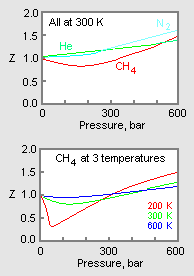
Figura 1: Exemple de grafice ale factorilor de compresibilitate a gazelor

Factorul de compresibilitate (Z) este o proprietate termodinamică utilă pentru modificarea legii gazelor ideale pentru a ține cont de comportamentul gazelor reale. Este o măsură a cât de mult se abat proprietățile termodinamice ale unui gaz real de la cele așteptate de la un gaz ideal. Poate fi considerată ca fiind raportul dintre volumul real al unui gaz real și volumul prezis de gazul ideal la aceeași temperatură și presiune ca și volumul real.

Pentru un gaz ideal, Z are întotdeauna o valoare de 1. Pentru gazele reale, valoarea poate devia pozitiv sau negativ, în funcție de efectul forțelor intermoleculare ale gazului. Cu cât un gaz real este mai aproape de punctul său critic sau de punctul său de saturație, cu atât mai mari sunt abaterile gazului de la comportamentul ideal.

Graficul superior din figura 1 ilustrează modul în care variază factorul de compresibilitate pentru diferite gaze la aceeași temperatură și presiune. Graficul de jos ilustrează modul în care factorul de compresibilitate al unui gaz (de exemplu, metanul) la o presiune dată variază cu temperatura.

Acest articol se ocupă numai de factorul de compresibilitate al gazelor și nu aprofundează compresibilitatea lichidelor sau a amestecurilor vapori-lichid.

Contenit

1 Determinarea valorilor de compresibilitate a gazelor
- 1.1 Grafice generalizate ale factorului de compresibilitate pentru gaze pure
- 1.2 Grafice generalizate ale factorului de compresibilitate pentru amestecuri de gaze
- 1.3 Ecuația lui van der Waals
  - 1.3.1 Versiuni modificate ale ecuației lui van der Waals
    - 1.3.1.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Ecuația de stare virială
- 1.5 Alte ecuații de stare
- 1.6 Notații pentru constanta gazelor
2 Referințe

Determinarea valorilor compresibilității gazelor

Legea gazelor ideale se definește astfel:

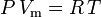
$P\,V_\mathrm{m} = R\,T$

și legea gazului ideal corectată pentru non-idealitate se definește astfel:

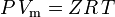
$P\,V_\mathrm{m} = ZR\,T$

unde:
P	= presiunea
Vm	= volumul molar al gazului
Z	= factorul de compresibilitate
R	= constanta universală a gazelor
T	= temperatura

și astfel:

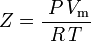
$Z = \frac{\;P\,V_\mathrm{m}}{R\,T}$

care este cea mai simplă și cea mai larg utilizată ecuație de stare a gazelor reale (EOS). Limitarea majoră a acestei ecuații de stare constă în faptul că factorul de compresibilitate a gazului, Z, nu este o constantă, ci variază de la un gaz la altul, precum și în funcție de temperatura și presiunea gazului în cauză. Acesta trebuie determinat experimental.

Dacă sunt disponibile date experimentale pentru anumite gaze, aceste date pot fi utilizate pentru a produce grafice (cum ar fi în figura 1) ale lui Z în funcție de presiune la o temperatură constantă sau ale lui Z în funcție de presiune pentru diferite temperaturi pentru acele gaze specifice. Astfel de grafice sunt utile pentru a obține cu ușurință valori interpolate ale lui Z între valorile determinate experimental.

Factorul de compresibilitate, așa cum s-a menționat mai devreme, poate fi, de asemenea, exprimat ca:

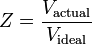
$Z = \frac{V_\mathrm{real}}{V_\mathrm{ideal}}$

Există trei regimuri care afectează factorul de compresibilitate:

valoarea lui Z tinde spre 1 pe măsură ce presiunea gazului se apropie de 0, unde toate gazele tind spre un comportament ideal
valoarea lui Z este mai mică decât 1 la presiuni intermediare deoarece forțele de atracție intermoleculare fac ca volumele reale să fie mai mici decât valorile ideale
valoarea lui Z este mai mare decât 1 și tinde în cele din urmă spre infinit la presiuni ridicate, deoarece forțele intermoleculare de respingere determină ca volumele reale să fie mai mari decât valorile ideale

Grafice generalizate ale factorului de compresibilitate pentru gaze pure

Relația unică dintre factorul de compresibilitate și temperatura redusă, Tr, și presiunea redusă, Pr, a fost recunoscută pentru prima dată de van der Waals în 1873 și este cunoscută sub numele de principiul celor doi parametri ai stărilor corespunzătoare. Principiul stărilor corespunzătoare exprimă generalizarea conform căreia proprietățile unui gaz care depind de forțele intermoleculare sunt legate de proprietățile critice ale gazului într-un mod universal. Aceasta oferă o bază extrem de importantă pentru dezvoltarea corelațiilor proprietăților moleculare.

În ceea ce privește compresibilitatea gazelor, principiul stărilor corespunzătoare indică faptul că orice gaz pur la aceeași temperatură redusă, Tr, și presiune redusă, Pr, ar trebui să aibă același factor de compresibilitate.

Temperatura și presiunea redusă se definesc astfel:

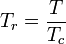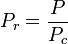
$T_r = \frac{T}{T_c}$ și $P_r = \frac{P}{P_c}$

Tc și Pc sunt cunoscute ca temperatura și presiunea critică a unui gaz. Acestea sunt caracteristici ale fiecărui gaz în parte, Tc fiind temperatura peste care nu este posibilă lichefierea unui anumit gaz, iar Pc este presiunea minimă necesară pentru a lichefia un anumit gaz la temperatura sa critică. Împreună, ele definesc punctul critic al unui fluid peste care nu există faze distincte lichide și gazoase ale unui anumit fluid.

Datele de presiune-volum-temperatură (PVT) pentru gazele reale variază de la un gaz pur la altul. Cu toate acestea, atunci când factorii de compresibilitate ai diferitelor gaze cu un singur component sunt reprezentați grafic în funcție de presiune împreună cu izotermele de temperatură (așa cum se arată pentru metan în graficul inferior din figura 1), multe dintre grafice prezintă forme izoterme similare.

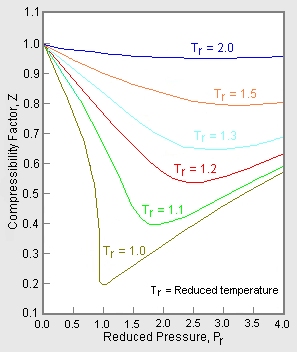
Figura 2: Exemplu de grafic generalizat al factorului de compresibilitate

Pentru a obține un grafic generalizat care poate fi utilizat pentru multe gaze diferite, presiunea și temperatura reduse, Pr și Tr, sunt utilizate pentru a normaliza datele factorului de compresibilitate. Figura 2 este un exemplu de grafic generalizat al factorului de compresibilitate derivat din sute de puncte de date P-V-T experimentale pentru 10 gaze pure, și anume metan, etan, etenă, etilenă, propan, n-butan, i-pentan, i-pentan, n-hexan, azot, dioxid de carbon și abur.

Există grafice mai detaliate ale factorilor de compresibilitate generalizate bazate pe până la 25 sau mai multe gaze pure diferite, cum ar fi graficele Nelson-Obert. Se spune că astfel de grafice au o precizie de 1-2 procente pentru valori Z mai mari de 0,6 și de 4-6 procente pentru valori Z de 0,3-0,6.

Graficele generalizate ale factorului de compresibilitate pot fi considerabil eronate pentru gazele puternic polare, care sunt gaze pentru care centrele de sarcină pozitivă și negativă nu coincid. În astfel de cazuri, estimarea pentru Z poate fi eronată cu până la 15-20%.

Gazele cuantice hidrogen, heliu și neon nu se conformează comportamentului stărilor corespunzătoare și presiunea și temperatura redusă pentru aceste trei gaze ar trebui redefinite în felul următor pentru a îmbunătăți precizia predicției factorilor lor de compresibilitate atunci când se utilizează graficele generalizate:

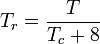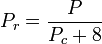
$T_r = \frac{T}{T_c + 8}$ și $P_r = \frac{P}{P_c + 8}$

unde temperaturile sunt în grade Kelvin și presiunile sunt în atmosfere.

Grafice generalizate ale factorului de compresibilitate pentru amestecuri de gaze

Graficele generalizate ale factorului de compresibilitate pentru gaze pure (cum ar fi cele exemplificate în figura 2 sau graficele Nelson-Obert pot fi, de asemenea, utilizate pentru amestecuri de gaze prin utilizarea regulii lui Kay propusă de W. B. Kay în 1936. Această regulă prezice comportamentul P-V-T al unui amestec de gaze prin determinarea factorului de compresibilitate pentru un amestec de gaze la temperatura redusă și la presiunea redusă definite în termeni de temperatură pseudocritică, Tpc și presiune pseudocritică, Ppc care sunt definite astfel:

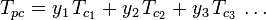
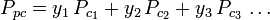
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3}\,\dots$ $P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3}\,\dots$

unde:
Tpc	= temperatura pseudocritică a amestecului de gaze
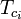$T_{c_i}$	= temperatura critică a unui component al amestecului de gaze
Ppc	= temperatura pseudocritică presiune a amestecului de gaze
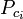$P_{c_i}$	= temperatura critică a unui component al gazului
yi	= fracția molară (sau de volum) a unui component al gazului

Temperatura pseudoreduită, Tpr, și presiunea pseudoreduită, Ppr, care se utilizează cu graficele factorului de compresibilitate generalizat pentru gazele pure sunt atunci:

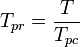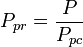
$T_{pr} = \frac{T}{T_{pc}}$ și $P_{pr} = \frac{P}{P_{pc}}$

Un grafic al factorului de compresibilitate pentru gazul natural (care este un amestec de hidrocarburi și alte gaze) folosind temperaturi și presiuni pseudoreducute este disponibil pe internet.

Ecuația lui van der Waals

Ecuația lui van der Waals a fost dezvoltată în 1873 și poate fi exprimată astfel:

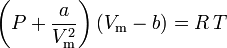
$\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T$

unde:

a este o măsură a puterii de atracție dintre moleculele de gaz b ține cont de volumul ocupat de moleculele de gaz, ceea ce scade volumul deschis disponibil

Ecuația lui van der Waals poate fi rearanjată astfel:

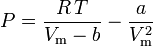
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

și factorul de compresibilitate poate fi scris ca:

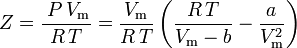
$Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_mathrm{m}}{R\,T}\left(\frac{R\,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2}\right)$

și avem acum o ecuație pentru determinarea lui Z folosind parametrii van der Waals a și b:

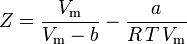
$Z = \frac{V_\mathrm{m}}{V_mathrm{m}} - b} - \frac{a}{R\,T\,V_\mathrm{m}}$

Deși a și b sunt denumite „constantele Van der Waals”, ele nu sunt cu adevărat constante, deoarece variază de la un gaz la altul; ele sunt, totuși, independente de P, V și T. Cu alte cuvinte, ele sunt constante pentru gazul considerat. Date fiind temperatura și presiunea critică pentru un anumit gaz, a și b pot fi obținute pentru acel gaz specific din aceste ecuații:

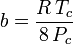
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ și $b = \frac{R\, T_c}{8\, P_c}$

De exemplu, presiunea critică a etanului este 4.884 MPa, iar temperatura critică este de 305,43 K (32,3˚C). Utilizând constanta universală a gazelor, R, de 8,3145 Pa m3 K-1 mol-1, ecuațiile de mai sus dau a = 0,557 m6 Pa mol-2 și b = 6,500×10-5 m3 mol-1.

Valorile tabelate ale lui a și b pentru diferite gaze sunt disponibile în aceste referințe, precum și în multe alte surse din literatura tehnică.

Versiuni modificate ale ecuației van der Waals

Determinarea factorilor de compresibilitate prin utilizarea ecuației de stare van der Waals reprezintă o îmbunătățire față de utilizarea graficelor de compresibilitate generalizate. Cu toate acestea, există versiuni modificate ale ecuației de stare van der Waals care oferă o îmbunătățire și mai mare. Poate că cele mai utilizate ecuații de stare de către inginerii care lucrează în rafinarea petrolului, producția petrochimică, prelucrarea gazelor naturale, distilarea criogenică și alte industrii conexe sunt: ecuația Redlich-Kwong dezvoltată în 1949, ecuația Soave-Redlich-Kwong dezvoltată în 1972 și ecuația Peng-Robinson dezvoltată în 1976. Aceste trei ecuații sunt, în esență, versiuni modificate ale ecuației van der Waals. Ecuațiile comparative sunt:

Redlich-Kwong

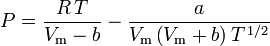
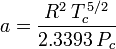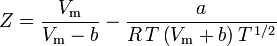
$P = \frac{R\,T}{V_\mathrm{m}{m} - b} - \frac{a}{V_\mathrm{m}\stânga(V_\mathrm {m} + b\-dreapta)T^{\,1/2}}$ $a = \frac{R^2\, T_c^{\,5/2}}}{2.3393\\, P_c}$ și $b = \frac{R\, T_c}{11.5420\\\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}$

Soave-Redlich-Kwong

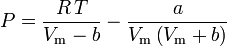
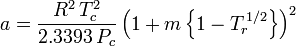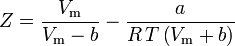
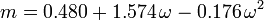
$P = \frac{R\,T}{V_\mathrm{m}{m} - b} - \frac{a}{V_\mathrm{m}\stânga(V_\mathrm {m} + b\dreapta)}$ $a = \frac{R^2\,T_c^2}{2.3393\\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big)^2$ și $b = \frac{R\\, T_c}{11.5420\\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}$ $m = 0.480 + 1,574\\, \omega - 0,176\, \omega^2$

Factorul acentric, ω, utilizat ca parametru în ecuațiile Soave-Redlich-Kwong și Peng-Robinson a fost introdus pentru prima dată de Pitzer et al. în 1955. Acesta poate fi exprimat ca:

\omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}\right) – 1

unde Pvp este presiunea de vapori saturați a gazului la o temperatură de 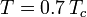$T = 0,7\, T_c$ .

Peng-Robinson

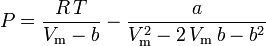
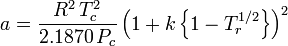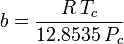
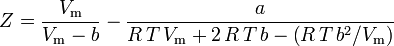
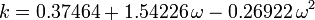
$P = \frac{R\,T}{V_\mathrm{m}{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}$ $a = \frac{R^2\,T_c^2}{2.1870\\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2$ și $b = \frac{R\, T_c}{12.8535\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_mathrm{m} + 2\,R\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}$ $k = 0.37464 + 1.54226\, \omega - 0.26922\, \omega^2$

Ecuația de stare virială

Cea mai fundamentală ecuație de stare , în sensul că are cea mai solidă bază teoretică, este ecuația de stare virială:

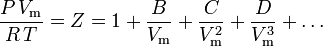
$\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}}. + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots$

A fost propusă pentru prima dată pe o bază empirică de Thiesen în 1885 și dezvoltată în continuare în 1901 de Kamerlingh-Onnes. O expresie statistico-mecanică pentru B a fost derivată pentru prima dată de Ornstein în teza sa de doctorat. Ecuația a fost ulterior reelaborată de H.D. Ursell în 1927 pe o bază teoretică derivată dintr-o analiză statistico-mecanică (cluster) a forțelor intermoleculare.

Parametrii B, C și D sunt denumiți al doilea, al treilea și, respectiv, al patrulea coeficient virial. Coeficienții nu sunt constanți, deoarece variază de la un gaz la altul, precum și temperatura gazului considerat. Aceștia se scriu uneori ca B(T), C(T) și D(T) pentru a indica faptul că sunt funcții de temperatură. Valoarea numerică a coeficienților trebuie să fie determinată experimental.

Cel de-al doilea coeficient virial asigură cea mai mare parte a corecției pentru comportamentul neideal al unui gaz. Din acest motiv, ecuația virială este uneori trunchiată după termenul care conține cel de-al doilea coeficient. Cu toate acestea, atunci când este disponibil cel de-al treilea coeficient, ecuația este de obicei trunchiată după termenul care conține cel de-al treilea coeficient. Cel de-al patrulea coeficient este rareori disponibil.

O compilație extinsă de coeficienți viriali pentru gaze pure și amestecuri de gaze a fost pregătită din baza de date a coeficienților viriali de la Thermodynamics Research Center, fostă Texas A&M University, College Station, Texas și acum localizată la National Institute of Standards and Technology (NIST), Boulder, Colorado. Cea mai recentă versiune a acestei compilații a fost publicată în 2003. NIST oferă, de asemenea, spre achiziționare un program software, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), care include al doilea și al treilea coeficient virial, precum și o multitudine de alte proprietăți termodinamice.

Alte ecuații de stare

Există o serie de alte ecuații de stare pentru prezicerea comportamentului gazelor reale. Poate, cele mai cunoscute sunt ecuația Beattie-Bridgeman dezvoltată în 1929 și ecuația Benedict-Rubin-Webb dezvoltată în 1940. În general, acestea sunt mai complexe decât ecuațiile discutate mai sus.

Noțiune pentru constanta gazelor

Constanta gazelor utilizată în acest articol este constanta universală a gazelor, R, care se aplică oricărui gaz. Există, de asemenea, o constantă specifică a gazelor, care poate fi notată cu Rs, și este definită ca Rs = R / M, unde M este greutatea moleculară.

Din păcate, mulți autori din literatura tehnică folosesc uneori R ca și constantă specifică a gazelor fără să o denumească ca atare sau să precizeze că aceasta este constanta specifică a gazelor. Acest lucru poate duce și duce la confuzii.

1.0 1.1 1.1 1.2 1.3 1.4 McQuarrie, Donald A. și Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X.

2.0 2.1 2.2 2.2 2.3 2.4 Yunus A. Çengal și Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, ediția a doua. McGraw-Hill Professional. ISBN 0-07-245426-1.

3.0 3.1 3.2 3.3 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, ediția a șaptea. McGraw Hill. ISBN 0-07-310445-0.

4.0 4.1 4.2 4.3 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Termodinamica ingineriei chimice. Universities Press (India). ISBN 81-7371-048-1.

5.0 5.1 Legile gazelor (Prelegere susținută de profesorul M.J. Mombourquette la Universitatea Queens, Canada)

Hong Wei Xiang (2005). Principiul stărilor corespondente și practica sa: Thermodynamic, Transport and Surface Properties of Fluids (Proprietăți termodinamice, de transport și de suprafață ale fluidelor). Elsevier. ISBN 0-444-52062-7.

IUPAC Goldbook

Gouq-Jen Su (1946). „Modified Law of Corresponding States” (Legea modificată a stărilor corespondente). Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.

9.0 9.1 Ecuații de stare (Profesor Lyes Kadem, Universitatea Concordia, Canada)

10.0 10.1 Ecuații de stare (Material de curs folosit de profesorul Sanford Klein de la Universitatea din Wisconsin-Madison, S.U.A.)

Richard W. Miller (1996). Flow Measurement Engineering Handbook, ediția a 3-a. McGraw-Hill. ISBN 0-07-04-042366-0. (Vezi Figura G-1 la pagina G.145)

Kai-Fui Vincent Wong (2000). Termodinamică pentru ingineri, Ediția I. CRC Press. ISBN 0-8493-0232-3. (Vezi Figura A-2, pagina 278}

Nelson-Obert Generalized Compressibility Charts (Grafice disponibile pe Internet, de pe site-ul Universității de Stat din San Diego, S.U.A.)

W.B.Kay (1936). „Gases and Vapors At High Temperature and Pressure – Density of Hydrocarbon” (Gaze și vapori la temperaturi și presiuni ridicate – Densitatea hidrocarburilor). Inginerie industrială & Chimie 28:1014. ISSN 0096-4484.

Yunus A. Çengal și Michael A. Bowes (2005). Termodinamica: An Engineering Approach, ediția a 5-a. McGraw-Hill. ISBN 0-07-2884959.

Real Gases (Material de curs folosit de profesorul R.M. Price la Universitatea Christian Brothers, S.U.A.)

Properties of Natural Gases (Profesor Jon Steiner Gudmandsson, Universitatea Norvegiană de Știință și Tehnologie)

Robert C. Weast (Editor) (1975). Manual de chimie și fizică, ediția a 56-a. (Handbook of Chemistry and Physics, 56th Edition). CRC Press. ISBN 0-87819-455-X.

19.0 19.1 19.2 19.2 Capitolul 3: Ecuații de stare (paginile 6-8 din 65 pagini pdf) (Parte a tezei de doctorat de Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)

20.0 20.1 20.2 Jean Vidal (2003). Thermodynamics: Aplicații în ingineria chimică și în industria petrolieră. Editions Technip. ISBN 2-7108-0800-5.

Zakia Nasri și Housam Binous (2007). „Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Recuperat de aici.

K.S. Pitzer et al. (1955). „The Volumetric and Thermodynamic Properties of Fluids” (Proprietățile volumetrice și termodinamice ale fluidelor). Journal of the American Chemical Society 77: 3427-3440.

Francis S. Manning și Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.

Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)

Max F. Thiesen (1885). „Investigations of the Equation of State” (Investigații privind ecuația de stare). Annalen der Physik und Chemie (24): 467-492.

Heike Kamerlingh-Onnes (1901). „Expression of the Equation of State of Gases and Liquids by Means of Series”. Commun. Phys. Lab. Leiden (71).

S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Application of the statistical mechanics of Gibbs on molecular-theoretical problems), Leiden

H. D. Ursell (1927). „The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.

J.D. Dymond și R.C. Wilhoit (autori), K.N. Marsch și M. Fenkel (editori) (2003). Virial Coefficients of Pure gases and Mixtures, 1st Edition. Springer. ISBN 3-540-4434040-1.

NIST Standard Reference Database 23

J.A. Beattie and O.C. Bridgeman (1929). „A New Equation of State for Fluids” (O nouă ecuație de stare pentru fluide). Proc. Amer. Acad. Arts Sci. (63): 229-305.

M. Benedict, G.B. Webb și L.C. Rubin (1940). „An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures” (O ecuație empirică pentru proprietățile termodinamice ale hidrocarburilor ușoare și ale amestecurilor lor). J. Chem. Phys. 8: 334-335.

Este posibil ca o parte din conținutul acestei pagini să fi apărut anterior pe Citizendium.

Retrasmis din „http://knowino.org/wiki/Compressibility_factor_(gases)”

Categorie: Fizică