O matrice de confuzie este un tabel care este adesea utilizat pentru a descrie performanța unui model de clasificare (sau „clasificator”) pe un set de date de test pentru care se cunosc valorile reale. Matricea de confuzie în sine este relativ simplu de înțeles, dar terminologia aferentă poate fi confuză.
Am vrut să creez un „ghid de referință rapidă” pentru terminologia matricelor de confuzie deoarece nu am putut găsi o resursă existentă care să corespundă cerințelor mele: prezentare compactă, folosind numere în loc de variabile arbitrare și explicată atât în termeni de formule, cât și de propoziții.
Să începem cu un exemplu de matrice de confuzie pentru un clasificator binar (deși poate fi ușor extins la cazul a mai mult de două clase):
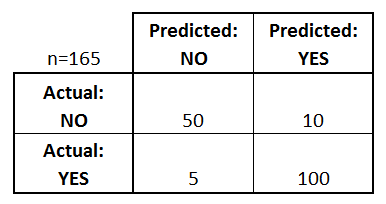
Ce putem învăța din această matrice?
- Există două clase prezise posibile: „da” și „nu”. Dacă am prezice prezența unei boli, de exemplu, „da” ar însemna că au boala, iar „nu” ar însemna că nu au boala.
- Clasificatorul a făcut un total de 165 de predicții (de ex, 165 de pacienți au fost testați pentru prezența acelei boli).
- Din aceste 165 de cazuri, clasificatorul a prezis „da” de 110 ori și „nu” de 55 de ori.
- În realitate, 105 pacienți din eșantion au boala, iar 60 de pacienți nu o au.
Să definim acum cei mai de bază termeni, care sunt numere întregi (nu rate):
- adevărați pozitivi (TP): Acestea sunt cazuri în care am prezis că da (au boala), și chiar au boala.
- adevărați negativi (TN): Am prezis nu, și nu au boala.
- false pozitive (FP): Am prezis da, dar ei nu au de fapt boala. (Cunoscută și sub numele de „eroare de tip I.”)
- false negative (FN): Am prezis că nu, dar ei au de fapt boala. (Cunoscută și sub numele de „eroare de tip II”)
Am adăugat acești termeni în matricea de confuzie și, de asemenea, am adăugat totalurile rândurilor și coloanelor:
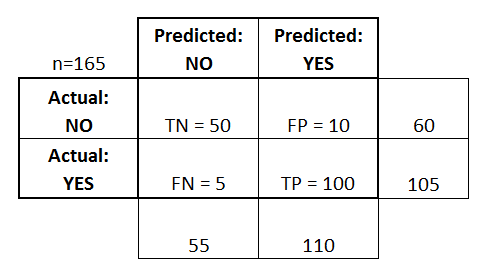
Aceasta este o listă de rate care sunt adesea calculate dintr-o matrice de confuzie pentru un clasificator binar:
- Precizie: În general, cât de des este corect clasificatorul?
- (TP+TN)/total = (100+50)/165 = 0,91
- Rata de neclasificare: În general, cât de des se greșește?
- (FP+FN)/total = (10+5)/165 = 0,09
- echivalent cu 1 minus Accuracy
- cunoscută și ca „Error Rate”
- True Positive Rate: Atunci când este de fapt da, cât de des prezice da?
- TP/da real = 100/105 = 0,95
- cunoscută și ca „Sensibilitate” sau „Recall”
- Rata falsului pozitiv: Atunci când este de fapt nu, cât de des prezice da?
- FP/nu real = 10/60 = 0,17
- Rata Adevărat Negativ: Când este de fapt nu, cât de des prezice nu?
- TN/nu real = 50/60 = 0,83
- echivalent cu 1 minus rata falsului pozitiv
- cunoscută și sub numele de „specificitate”
- Precizie: Când prezice da, cât de des este corect?
- TP/predicție da = 100/110 = 0,91
- Prevalența: Cât de des apare de fapt condiția da în eșantionul nostru?
- Da real/total = 105/165 = 0,64
Câțiva alți termeni merită, de asemenea, menționați:
- Rata de eroare nulă: Aceasta este frecvența cu care ați greși dacă ați prezice întotdeauna clasa majoritară. (În exemplul nostru, rata de eroare nulă ar fi 60/165=0,36, deoarece dacă ați prezice întotdeauna da, ați greși doar pentru cele 60 de cazuri „nu”). Aceasta poate fi o măsură de referință utilă pentru a vă compara clasificatorul. Cu toate acestea, cel mai bun clasificator pentru o anumită aplicație va avea uneori o rată de eroare mai mare decât rata de eroare nulă, după cum demonstrează Paradoxul Preciziei.
- Cohen’s Kappa: Aceasta este, în esență, o măsură a cât de bine a funcționat clasificatorul în comparație cu cât de bine ar fi funcționat prin simpla întâmplare. Cu alte cuvinte, un model va avea un scor Kappa ridicat dacă există o diferență mare între acuratețe și rata de eroare nulă. (Mai multe detalii despre Cohen’s Kappa.)
- Scorul F: Aceasta este o medie ponderată a ratei pozitive adevărate (recall) și a preciziei. (Mai multe detalii despre scorul F.)
- ROC Curve: Acesta este un grafic utilizat în mod obișnuit care rezumă performanța unui clasificator pe toate pragurile posibile. Se generează prin reprezentarea grafică a ratei adevăraților pozitivi (axa y) față de rata falșilor pozitivi (axa x) pe măsură ce variați pragul de atribuire a observațiilor la o anumită clasă. (Mai multe detalii despre curbele ROC.)
Și, în final, pentru cei din lumea statisticii bayesiene, iată un scurt rezumat al acestor termeni din Applied Predictive Modeling:
În legătură cu statistica bayesiană, sensibilitatea și specificitatea sunt probabilitățile condiționate, prevalența este prioritatea, iar valorile pozitive/negative prezise sunt probabilitățile posterioare.
Vreți să aflați mai multe?
În noul meu videoclip de 35 de minute, Making sense of the confusion matrix, explic aceste concepte mai în profunzime și abordez subiecte mai avansate:
- Cum să calculați precizia și reamintirea pentru probleme cu mai multe clase
- Cum să analizați o matrice de confuzie cu 10 clase
- Cum să alegeți metrica de evaluare potrivită pentru problema dumneavoastră
- De ce precizia este adesea o metrică înșelătoare
Spuneți-mi dacă aveți întrebări!