Sunt procese de învățare stocastice cu structură recurentă și stau la baza primelor tehnici de optimizare utilizate în RNA. Mașina Boltzmann a fost inventată de Geoffrey Hinton și Terry Sejnowski în 1985. Mai multă claritate poate fi observată în cuvintele lui Hinton despre Mașina Boltzmann.
„O caracteristică surprinzătoare a acestei rețele este că utilizează numai informațiile disponibile la nivel local. Schimbarea ponderii depinde doar de comportamentul celor două unități pe care le conectează, chiar dacă schimbarea optimizează o măsură globală.” – Ackley, Hinton 1985.
Câteva puncte importante despre Mașina Boltzmann –
-
Utilizează o structură recurentă.
-
Consistă din neuroni stocastici, care au una din cele două stări posibile, 1 sau 0.
-
Câțiva dintre neuronii din aceasta sunt adaptativi (stare liberă) și unii sunt fixați (stare înghețată).
-
Dacă aplicăm recoacerea simulată pe rețeaua discretă Hopfield, atunci aceasta ar deveni mașina Boltzmann.
Obiectivul mașinii Boltzmann
Obiectivul principal al mașinii Boltzmann este de a optimiza soluția unei probleme. Munca mașinii Boltzmann constă în optimizarea greutăților și a cantității legate de acea problemă particulară.
Arhitectura
Diagrama următoare prezintă arhitectura mașinii Boltzmann. Din diagramă reiese clar că aceasta este o matrice bidimensională de unități. Aici, ponderile pe interconexiunile dintre unități sunt -p unde p > 0. Ponderile autoconexiunilor sunt date de b unde b > 0.
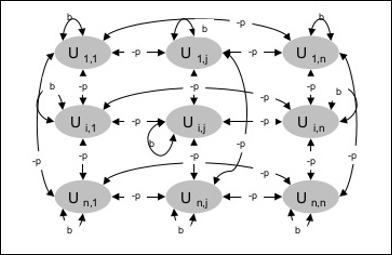
Algoritm de învățare
Cum știm că mașinile Boltzmann au ponderi fixe, prin urmare nu va exista un algoritm de învățare, deoarece nu este nevoie să actualizăm ponderile din rețea. Cu toate acestea, pentru a testa rețeaua, trebuie să stabilim ponderile, precum și să găsim funcția de consens (CF).
Mașina Boltzmann are un set de unități Ui și Uj și are conexiuni bidirecționale pe acestea.
-
Considerăm ponderea fixă, spunem wij.
-
wij ≠ 0 dacă Ui și Uj sunt conectate.
-
Există și o simetrie în interconectarea ponderată, i.e.adică wij = wji.
-
există și wii, adică ar exista autoconectarea între unități.
-
Pentru orice unitate Ui, starea ei ui ar fi fie 1, fie 0.
Obiectivul principal al mașinii Boltzmann este de a maximiza funcția de consens (CF) care poate fi dată de următoarea relație
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Acum, când starea se schimbă fie de la 1 la 0, fie de la 0 la 1, atunci modificarea consensului poate fi dată de următoarea relație –
$$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Aici ui este starea curentă a lui Ui.
Variația coeficientului (1 – 2ui) este dată de următoarea relație –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
În general, unitatea Ui nu-și schimbă starea, dar dacă o face, atunci informația ar fi rezidentă local în unitatea respectivă. Odată cu această schimbare, ar exista, de asemenea, o creștere a consensului rețelei.
Probabilitatea rețelei de a accepta schimbarea stării unității este dată de următoarea relație –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Aici, T este parametrul de control. Acesta va scădea pe măsură ce CF atinge valoarea maximă.
Algoritm de testare
Etapa 1 – Se inițializează următoarele pentru a începe antrenamentul –
- Ponderi care reprezintă constrângerile problemei
- Parametru de control T
Etapa 2 – Se continuă etapele 3-8, când condiția de oprire nu este adevărată.
Etapa 3 – Efectuați pașii 4-7.
Etapa 4 – Presupuneți că una dintre stări a schimbat ponderea și alegeți numerele întregi I, J ca valori aleatoare între 1 și n.
Etapa 5 – Calculați modificarea consensului după cum urmează –
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Etapa 6 – Calculați probabilitatea ca această rețea să accepte schimbarea de stare
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Etapa 7 – Acceptați sau respingeți această schimbare după cum urmează –
Cazul I – dacă R < AF, acceptați schimbarea.
Cazul II – dacă R ≥ AF, respingeți modificarea.
În acest caz, R este un număr aleator între 0 și 1.
Etapa 8 – Reduceți parametrul de control (temperatura) după cum urmează –
T(nou) = 0.95T(vechi)
Etapa 9 – Se testează condițiile de oprire care pot fi următoarele –
- Temperatura atinge o valoare specificată
- Nu există nici o schimbare de stare pentru un număr specificat de iterații
.