Bravais Lattices

Videnskab >Kemi >Feststof > Bravais Lattices

I denne artikel vil vi studere strukturerne af Bravais Lattices.

En krystal er en homogen del af et fast stof, der består af et regelmæssigt mønster af strukturelle enheder, der er bundet sammen af plane flader, der danner en bestemt vinkel med hinanden.

Enhedscelle:

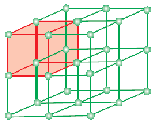
En enhedscelle er den mindste strukturelle gentagende enhed i et krystallinsk fast stof (rumgitter). Når enhedsceller af det samme krystallinske stof gentages i rummet i alle retninger, dannes der et krystallinsk fast stof. Enhedscellen repræsenteres på papir ved at tegne linjer, der forbinder de enkelte partiklers centre.

Den geometriske form, der kun består af en regelmæssig række af punkter i rummet, kaldes gitter eller rumgitter. Det kan defineres som en række punkter, der viser, hvordan molekyler, atomer eller ioner er anbragt på forskellige steder i et tredimensionelt rum. Hvert punkt i skæringspunktet mellem linjerne i enhedscellen repræsenterer en konstituerende partikel, dvs. et molekyle, et atom eller en ion. Dette skæringspunkt mellem linjerne i enhedscellen kaldes gitterpunkt eller gittersted.

Note: Hvert gitterpunkt i krystalgitteret har samme omgivelser eller miljø. To eller flere krystallinske stoffer kan have samme gitterplads. Hver eneste partikel i matrixen er altid repræsenteret ved et gitterpunkt i den tredimensionelle matrix.

Kendetegn ved krystalgitteret:

• Krystalgitteret er et regelmæssigt arrangement af bestanddelene i et krystallinsk fast stof i det tredimensionelle rum.
• Det består af et stort antal enhedsceller.
• Krystalgitteret defineres ud fra enhedscellens egenskaber.
• Ved opbrydning danner det mange enhedsceller.
• Et krystalgitter kan fremstilles, håndteres og studeres i et laboratorium under eksperimenter.
• Det er en makroskopisk egenskab.

Karakteristika ved enhedscelle:

• En enhedscelle er den mindste strukturelle gentagende enhed i et krystallinsk fast stof.
• Det er den grundlæggende enhed i krystalgitteret, som besidder alle krystallens egenskaber.
• Enhedscellen definerer de grundlæggende egenskaber krystalgitteret.
• Enhedsceller er en grundlæggende enhed, og kan derfor ikke opdeles yderligere.
• Enhedscellen er et hypotetisk begreb Derfor kan den ikke opnås under eksperimenter.
• Det er en mikroskopisk egenskab.

Typer af rumgitter:

Endimensionelt gitter:

I dette gitter findes der et sæt punkter, der er arrangeret med lige store afstande langs.

To dimensionelt gitter:

I denne type er der angivet to sider og vinklen mellem dem. Der findes fem typer to-dimensionelle gitter.

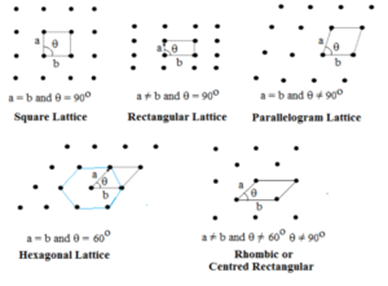
Hexagonalt gitter er en rhombe med θ = 60°

Bravais-gitter:

Lad længderne af tre kanter af enhedscellen være a, b og c. Lad α være vinklen mellem side b og c. Lad β være vinklen mellem side a og c. Lad γ være vinklen mellem side a og b.

Den franske matematiker Bravais sagde, at for forskellige værdier af a, b, c og α, β, γ, er der maksimalt fjorten (14) strukturer mulige. Disse arrangementer kaldes Bravais-netværk.

14 Bravais-netværk:

Sr. Nr.	Krystal System	Space Lattice Type	Diagram	Kantlængder	Vinkler	Eksempler
	Kubisk	Enkel primitive		a = b = c	α = β = γ = γ = 90°	Polonium (Po)
	Kubisk	Krop centreret		a = b = c	α = β = γ = 90°	Iron (Fe), Rubidium (Rb), Natrium (Na), Titanium (Ti), Vungsten (W), Uranium (U), Zirconium (Zr)
	Kubisk	Facet centreret		a = b = c	α = β = γ = γ = 90°	Kobber (Cu), Aluminium (Al), Nikkel (Ni), Guld (Au), Sølv (Ag), Platin (Pt)
	Tetragonal	Enkel primitive		a = b ≠ c	α = β = γ = γ = 90°	SnO2
	Tetragonal	Krop centreret		a = b ≠ c	α = β = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombisk	Enkel primitive		a ≠ b ≠ c	α = β = γ = 90°	Rhombisk svovl
	Orthorhombisk	Krop centreret		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombisk	Face centreret		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Orthorhombisk	Endcentreret ende		a ≠ b ≠ c	α = β = γ = γ = 90°	MgSO4, 7H2O
	Monoklin	simpel primitive		a ≠ b ≠ c	α =γ = 90° og β ≠ 90°	Monoklin svovl
	Monoklin	Endcentreret ende		a ≠ b ≠ c	α =γ = 90° og β ≠ 90	Na2SO4. 10H2O
	Triklinisk	simpel primitive		a ≠ b ≠ c	α =γ = 90° og β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonalt	Enkel primitive		a = b ≠ c	α = β = 90° og γ = 120°	ZnO, BeO, CoS, SnS
	Romboedrisk	Enkel primitive		a ≠ b ≠ c	α = β = γ ≠ 90°	Calcit, NaNO3, FeCO3

Partikel på hjørne:

Partiklen i hjørnet af enhedscellen er delt af 8 enhedsceller (4 lag under og 4 lag over). Derfor er hver enhedscelle 1/8 partikel.

Partikel på forsiden:

Partiklen på forsiden af enhedscellen deles af 2 tilstødende enhedsceller. Derfor er hver enhedscelle 1/2 partikel.

Partikel på kanten:

Partiklen på kanten af enhedscellen deles af 4 enhedsceller (2 lag under og 2 lag over). Derfor er hver enhedscelle 1/4 partikel.

Koordineringsnummer:

Koordineringsnummeret for den enkelte partikel i krystalgitteret er antallet af partikler, der omgiver en enkelt partikel i et krystalgitter.

Højere koordinationsnummeret er tættere partiklerne er pakket i krystalgitteret. Koordineringstallet er et mål for krystallens hårdhed.

Antal partikler i enhedscellen og koordineringstal

Simple Cubic Structure (scc):

Fra strukturen kan vi se, at der er 8 partikler i 8 hjørner af enhedscellen.Hver hjørnepartikel er delt af 8 naboenhedsceller. Derfor indeholder hver enhedscelle 1/8 af partiklen i dens hjørne.
Antal hjørner = 8, derfor antal partikler i enhedscellen = 1/8x 8 = 1

Hver partikel i denne struktur er direkte i kontakt med fire andre partikler i dens plan og en partikel i laget over og laget under. Hencetkoordineringstallet for simpel kubisk struktur er 4+ 1+ 1 = 6

Body-Centred Cubic Structure (bcc):

Fra strukturen kan vi se, at der er 8 partikler ved 8 hjørner af enhedscellen.Hver hjørnepartikel er delt af 8 naboenhedsceller. Derfor indeholder hver enhedscelle 1/8 af partiklen i dens hjørne. Antal hjørner = 8, derfor er antallet af partikler i enhedscellen i hjørnerne = 1/8 x 8 = 1

Til samme tid er der et atom i midten af cellen, derfor er antallet af partikler i enhedscellen 1 + 1 = 2

Hver partikel i denne struktur er direkte i kontakt med fire andre partikler i laget over og fire partikler i laget under. Derfor er koordineringstallet for den kropscentrerede kubiske struktur 4 + 4 = 8

FaceCentered Cubic Structure (fcc):

Fra strukturen kan vi se, at der er 8 partikler ved 8 hjørner af enhedscellen. Hver hjørnepartikel deles af 8 andre naboenhedsceller. Derfor indeholder hver enhedscelle 1/8 af partiklen i dens hjørne. Antallet af hjørner = 8. Derfor er antallet af partikler i en enhedscelle på hjørnerne = 1/8 x 8 = 1

Der er 6partikler på 6 flader i enhedscellen. Hver partikel på hver side deles af 2 naboenhedsceller. Derfor indeholder hver enhedscelle 1/2 af partiklen på dens flade.
Antal flader = 6. Derfor er antallet af partikler på fladen = 1/2 x 6 = 3

Dermed er antallet af partikler i enhedscellen 1 + 3 = 4

Hver partikel i denne struktur er direkte i kontakt med 4 andre partikler i dens lag og med 4 partikler i laget over og 4 partikler i laget under. Derfor er koordineringstallet for en kubisk struktur med kantcentreret kubisk struktur 4 + 4 + 4 + 4 = 12

Noter:

For en kantcentreret partikel er den delt af 4 enhedsceller. Derfor består hver enhedscelle af 1/4 partikel Antallet af atomer pr. enhedscelle er i samme forhold som forbindelsens stoikiometri. Det hjælper derfor til at forudsige forbindelsens formel.

Naturvidenskab >Kemi > Faststof > Bravais-netværk