Science >Chimie >Etat solide >Réseaux de Bravais
Dans cet article, nous allons étudier les structures des réseaux de Bravais.
Un cristal est une portion homogène d’une substance solide constituée d’un motif régulier d’unités structurelles liées par des surfaces planes faisant un angle défini entre elles.
Cellule unitaire:
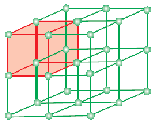
Une cellule unitaire est la plus petite unité structurelle répétitive d’un solide cristallin (réseau spatial). Lorsque les cellules unitaires d’une même substance cristalline sont répétées dans l’espace dans toutes les directions, un solide cristallin est formé. La cellule unitaire est représentée sur le papier en traçant des lignes reliant les centres des particules constitutives.
La forme géométrique consistant uniquement en un réseau régulier de points dans l’espace est appelée réseau ou treillis spatial. Il peut être défini comme un réseau de points montrant comment les molécules, les atomes ou les ions sont disposés dans différents sites, dans un espace tridimensionnel. Chaque point à l’intersection des lignes dans la cellule unitaire représente une particule constitutive, à savoir une molécule, un atome ou un ion. Ce point d’intersection des lignes dans la cellule unitaire est appelé point de réseau ou site de réseau.
Note : Chaque point de réseau dans le réseau cristallin a le même entourage ou environnement. Deux substances cristallines ou plus peuvent avoir le même espace de treillis. Chaque particule du réseau est toujours représentée par un point du réseau dans le réseau tridimensionnel.
Caractéristiques du réseau cristallin:
- Le réseau cristallin est un arrangement régulier des particules constitutives d’un solide cristallin dans un espace tridimensionnel.
- Il est constitué d’un grand nombre de cellules unitaires.
- Le réseau cristallin est défini en fonction des propriétés de la cellule unitaire.
- Lors de la rupture, il forme de nombreuses cellules unitaires.
- Un réseau cristallin peut être obtenu, manipulé et étudié en laboratoire lors d’expériences.
- C’est une propriété macroscopique.
Caractéristiques de la cellule unitaire:
- Une cellule unitaire est la plus petite unité structurelle répétitive d’un solide cristallin.
- C’est l’unité fondamentale du réseau cristallin qui possède toutes les propriétés du cristal.
- La cellule unitaire définit les propriétés fondamentales du réseau cristallin.
- Les cellules unitaires sont une unité fondamentale, donc ne peuvent pas être divisées davantage.
- Une cellule unitaire est un concept hypothétique D’où l’impossibilité de l’obtenir lors des expériences.
- C’est une propriété microscopique.
Types de treillis spatiaux:
Treillis à une dimension:
Dans ce treillis, il existe un ensemble de points disposés à des distances égales le long…

Treillis à deux dimensions:
Dans ce type, deux côtés et l’angle entre eux sont spécifiés. Il existe cinq types de treillis à deux dimensions.
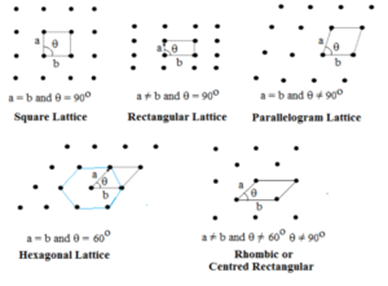
Le treillis hexagonal est un losange avec θ = 60°
Treillis de Bravais:

Les longueurs de trois bords de la cellule unitaire sont a, b et c. Soit α l’angle entre le côté b et c. Soit β l’angle entre les côtés a et c. Soit γ l’angle entre les côtés a et b.
Le mathématicien français Bravais a dit que pour différentes valeurs de a, b, c, et α, β, γ, maximum quatorze (14) structures sont possibles. Ces arrangements sont appelés treillis de Bravais.
14 treillis de Bravais :
|
Sr. No. |
Cristal Système |
Réseau spatial Type |
Diagramme |
Longueur des arêtes |
Angles |
Exemples |
|
Cubique |
Simple primitif . |
 |
a = b = c |
α = β = γ = 90° |
Polonium (Po) |
|
|
Cubique |
Corps centré |
 |
a = b = c |
α = β = γ = 90° |
Fer (Fe), Rubidium (Rb), Sodium (Na), Titanium (Ti), Tungstène (W), Uranium (U), Zirconium (Zr) |
|
|
Cubique |
Face centrée |
 |
a = b = c |
α = β = γ = 90° |
Cuivre (Cu), Aluminium (Al), Nickel (Ni), Or (Au), Argent (Ag), Platine (Pt) |
|
|
Tétragonal |
Simple primitif |
 |
a = b ≠ c |
α = β = γ = 90° . |
SnO2 |
|
|
Tétragonal |
Corps. centré |
 |
a = b ≠ c |
α = β = γ = 90° |
Ti, O2, CaSO4 |
|
|
Orthorhombique |
Simple . primitif |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
Soufre rhombique |
|
|
Orthorhombique |
Corps. centré |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
KNO3 |
|
|
Orthorhombique |
Face centrée |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
BaSO4 |
|
|
Orthorhombique |
End centré |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
MgSO4, 7H2O |
|
|
Monoclinique |
simple . primitif |
 |
a ≠ b ≠ c |
α =γ = 90° et β ≠ 90° |
Soufre monoclinique |
|
|
Monoclinique |
End centré |
 |
a ≠ b ≠ c |
α =γ = 90° et β ≠ 90 |
Na2SO4. 10H2O |
|
|
Triclinique |
simple primitif |
 |
a ≠ b ≠ c |
α =γ = 90° et β ≠ 90° |
K2Cr2O7, H3BO3 |
|
|
Hexagonal |
Simple primitif |
 |
a = b ≠ c |
α = β = 90° et γ = 120° |
ZnO, BeO, CoS, SnS |
|
|
Rhombohedral |
Simple primitif |
 |
a ≠ b ≠ c |
α = β = γ ≠ 90° |
Calcite, NaNO3, FeCO3 |
Particule au coin :

La particule au coin de la cellule unitaire est partagée par 8 cellules unitaires (4 couches en dessous et 4 couches au-dessus). D’où chaque cellule unitaire 1/8 particule.
Particule à la face:

La particule à la face de la cellule unitaire est partagée par 2 cellules unitaires adjacentes. D’où chaque cellule unitaire 1/2 particule.
Particule au bord:

La particule au bord de la cellule unitaire est partagée par 4 cellules unitaires (2 couches en dessous et2 couches au-dessus). Par conséquent, chaque cellule unitaire 1/4 de particule.
Nombre de coordination:
Le nombre de coordination de la particule constitutive du réseau cristallin est alors le nombre de particules entourant une seule particule dans un réseau cristallin.
Plus le nombre de coordination est élevé, plus les particules sont serrées dans le réseau cristallin. Le nombre de coordination est la mesure de la dureté du cristal.
Nombre de particules dans la cellule unitaire et nombre de coordination
Simple structure cubique (scc):

D’après la structure, nous pouvons voir qu’il y a 8 particules aux 8 coins de la cellule unitaire.Chaque particule de coin est partagée par 8 cellules unitaires voisines. Par conséquent, chaque cellule unitaire contient 1/8ème de la particule à son coin.
Nombre de coins = 8, Par conséquent, le nombre de particules dans la cellule unitaire = 1/8x 8 = 1
Chaque particule dans cette structure est directement en contact avec quatre autres particules dans son plan et une particule chacune dans la couche au-dessus et la couche en dessous. D’où le nombre de coordination pour la structure cubique simple est 4+ 1+ 1 = 6

Structure cubique centrée sur le corps (bcc):

D’après la structure, nous pouvons voir qu’il y a 8 particules aux 8 coins de la cellule unitaire.Chaque particule de coin est partagée par 8 cellules unitaires voisines. Par conséquent, chaque cellule unitaire contient 1/8ème de la particule à son coin. Nombre de coins = 8, d’où le nombre de particules dans la cellule unitaire aux coins = 1/8 x 8 = 1
En même temps, il y a un atome au centre de la cellule, D’où le nombre de particules dans la cellule unitaire 1 + 1 = 2
Chaque particule dans cette structure est directement en contact avec quatre autres particules dans la couche au-dessus et quatre particules dans la couche en dessous. Par conséquent, le nombre de coordination pour la structure cubique centrée sur le corps est 4 + 4 = 8

Structure cubique centrée sur la face (fcc):

D’après la structure, nous pouvons voir qu’il y a 8 particules aux 8 coins de la cellule unitaire. Chaque particule de coin est partagée par 8 autres cellules unitaires voisines. Par conséquent, chaque cellule unitaire contient 1/8ème de la particule à son coin. Le nombre de coins = 8. Par conséquent, le nombre de particules dans une cellule unitaire aux coins = 1/8 x 8 = 1
Il y a 6particules à 6 faces de la cellule unitaire. Chaque particule de face est partagée par 2 cellules unitaires voisines. D’où chaque cellule unitaire contient la moitié de la particule sur sa face.
Le nombre de faces = 6. D’où le nombre de particules sur la face = 1/2 x 6 = 3
D’où le nombre de particules dans la cellule unitaire 1 + 3 = 4
Chaque particule dans cette structure est directement en contact avec 4 autres particules dans sa couche et avec 4 particules dans la couche au-dessus et4 particules dans la couche en dessous. Par conséquent, le nombre de coordination pour la structure cubique à faces centrées est de 4 + 4 + 4 = 12

Notes:
Pour la particule à faces centrées, elle est partagée par 4 cellules unitaires. Par conséquent, chaque cellule unitaire est constituée de 1/4 de particule Le nombre d’atomes par cellule unitaire est dans le même rapport que la stœchiométrie du composé. Par conséquent, cela permet de prédire la formule du composé.
Science >Chimie >Etat solide >Réseaux de Bravais