I centri dei triangoli

Dove si trova il centro di un triangolo?

Ci sono in realtà migliaia di centri!

Ecco i 4 più popolari:

Centroide, Circumcentro, Incentro e Ortocentro

Per ognuno di questi, il “centro” è dove si incrociano linee speciali, quindi tutto dipende da quelle linee!

Guardiamo ognuno di essi:

Centroide

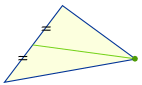Disegna una linea (chiamata “mediana”) da ogni angolo al punto medio del lato opposto. Il punto in cui tutte e tre le linee si intersecano è il centroide, che è anche il “centro di massa”:

Prova: taglia un triangolo di cartone, traccia le mediane. Si incontrano tutte in un punto? Puoi bilanciare il triangolo in quel punto?

Circumcentro

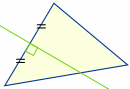Disegna una linea (chiamata “bisettrice perpendicolare”) perpendicolare al punto medio di ogni lato. Il punto in cui le tre linee si intersecano è il centro della “circonferenza” di un triangolo, chiamato “circocentro”:

Prova: trascina i punti qui sopra fino ad ottenere un triangolo rettangolo (ad occhio va bene). Dov’è il circocentro? Perché?

Incentro

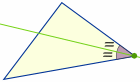Disegna una linea (chiamata “bisettrice dell’angolo”) da un angolo in modo che divida l’angolo a metà Il punto in cui le tre linee si intersecano è il centro dell'”incircolo” di un triangolo, chiamato “incentro”:

Prova questo: trova l’incentro di un triangolo usando un compasso e un righello a: Inscrivere un cerchio in un triangolo

Ortocentro

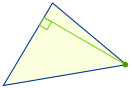Traccia un segmento di linea (chiamato “quota”) ad angolo retto con un lato che va all’angolo opposto. Il punto in cui tutte e tre le linee si intersecano è l'”ortocentro”:

Nota che a volte i bordi del triangolo devono essere estesi fuori dal triangolo per disegnare le quote. Allora l’ortocentro è anche fuori dal triangolo.