科学 > 化学 > 固体 > ブラベ格子
この記事では、ブラベ格子の構造について勉強しましょう。
結晶は、互いに一定の角度をなす平面によって結合された構造単位の規則的なパターンからなる固体物質の均質な部分である。
単位セル:
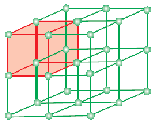
単位セルとは結晶性固体の最小構造繰り返し単位(空間格子)である。 同じ結晶性物質の単位セルが空間的に四方八方に繰り返されると、結晶性固体が形成される。
空間的に規則正しく並んだ点のみからなる幾何学的形態を格子または空間格子という。 分子、原子、イオンが3次元空間の異なる場所にどのように配置されているかを示す点の配列と定義することができる。 ユニットセル内の線の交点にある各点は、構成粒子viz.分子または原子またはイオンを表します。 注:結晶格子の各格子点は、同じ周囲または環境を持つ。 2つ以上の結晶体がthesame格子空間を持つことがあります。
結晶格子の特徴:
- 結晶格子は、3次元空間における結晶性固体の構成粒子の規則的な配列である。
- 結晶格子は、単位セルの特性で定義されます。
- 分割すると、多数の単位セルを形成します。
- 結晶格子は、実験室で入手、取り扱い、実験中に調べることが可能です。
- マクロな性質です。
単位格子の特徴:
- 単位格子は結晶性固体の最小の構造繰り返し単位で、結晶性固体を構成しています。
- 結晶格子の基本単位で、結晶のすべての性質を持ちます。
- 単位胞は基本単位なので、それ以上分割できません。
- 単位胞は仮説的概念なので、実験中に得ることはできません。
- ミクロな性質です。
空間格子の種類:
一次元格子:
この格子では、等間隔で並んだ点の集合が存在します。

二次元格子:
二辺とそれらの間の角度が指定されているものである。 2次元格子は5種類ある。
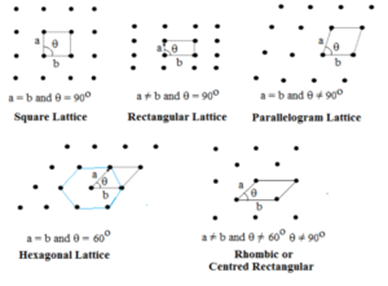
六角格子はθ=60°のひし形
Bravais Lattices:

単位セルの三つの辺の長さをa、b、cとする。 αは辺bとcのなす角、γは辺aとbのなす角とする。
フランスの数学者ブラベは、a、b、c、α、β、γの異なる値に対して、最大14の構造が可能であると言った。 これらの配置はブラベ格子と呼ばれる。
|
Sr. No. |
結晶 系 |
空間格子 型 |
Diagram |
辺長 |
例 |
|
|
立方体 |
単純 primitive |
 |
a = b = c |
α = beta = γ = 90° |
Polonium (Po) |
|
|
立方体 |
体中心 |
 |
a = b = c |
α = β =γ = 90° |
鉄(Fe).珪素(Cr), ルビジウム(Rb), ナトリウム(Na), チタン(Ti), タングステン(W), ウラン(U), イリジウム(U), イリジウム(U), ルビジウム(S),ルビジウム(S ジルコニウム(Zr) |
|
|
キュービック |
面心出し
|
a = b = c |
α = β = γ = 90° |
銅(Cu)である。 アルミニウム(Al), ニッケル(Ni), 金(Au), 銀(Ag)………………………………, 白金(Pt) |
||
|
正方形 |
単純な primitive |
 |
a = b ≠ c |
α=β=γ=90° |
SnO2 |
|
|
Tetragonal |
Body centred |
 |
a = b ≠ c |
α=β=γ=90° |
Ti, O2, CaSO4 |
|
|
斜方晶系 |
単純系 。 primitive |
 |
a≠b≠c |
α=β=γ=90° |
斜方硫黄 |
|
|
斜方体 |
体型 centred |
 |
a≠b≠c |
α=β=γ=90° |
KNO3 |
|
|
斜方形 |
面 centred |
 |
a≠b≠c |
α=β=γ=90° |
BaSO4 |
|
|
斜方晶 |
端面中心
|
a≠b≠c |
α=β=γ=90° |
MgSO4. 7H2O |
||
|
Monoclinic |
simple primitive |
 |
a≠b≠c |
α=γ=90° および β≠90° |
単斜硫黄 |
|
|
Monoclinic |
End Centred |
 |
a ≠ b ≠ c |
α =γ = 90°でβ ≠ 90 |
Na2SO4. 10H2O |
|
|
Triclinic |
simple primitive |
 |
a ≠ b ≠ c |
α =γ = 90°、β ≠ 90° |
||
|
Hexagonal |
Simple primitive |
 |
a = b ≠ c |
α = β = 90° および γ = 120° |
ZnO.の場合。 BeO, CoS, SnS |
|
|
Rhombohedral |
Simple primitive |
 |
a≠b≠c |
α=β=γ≠90° |
Calcite (カルサイト)。 NaNO3, FeCO3 |
コーナーにある粒子です。

単位格子の角の粒子は8つの単位格子(下の4層と上の4層)に共有されています。
面の粒子:

面の粒子は隣接する2つの単位セルで共有されます。
端の粒子:

端の粒子は下2層と上2層の合計4層で共有されます。
配位数:
結晶格子の構成粒子の配位数は、結晶格子の中で1つの粒子を取り囲む粒子の数であり、配位数が多いほど結晶格子の中で粒子が密に詰まっている。
単位格子の粒子数と配位数
単純立方構造(scc):

構造から、単位セルの8隅に8粒子があり、各隅粒子は隣接する8単位セルで共有していることがわかる。
Number of corners = 8, Hence number of particles in unit cell = 1/8x 8 = 1
この構造の各粒子は、その平面上で他の4粒子、上の層と下の層で各1粒子と直接接触している。 単純立方構造の配位数は4+ 1+ 1 = 6

体心立方構造(bcc):

構造から、ユニットセルの8隅に8個の粒子があることが分かる。各コーナー粒子は8つの隣接するユニットセルで共有される。 したがって、各単位セルには、その角の粒子の1/8が含まれていることになる。 角の数=8、したがって角の単位セルの粒子数=1/8×8=1
同時にセルの中心に原子があるので、単位セルの粒子数は1+1=2
この構造の各粒子は上の層で他の4粒子と下の層で4粒子と直接接触している。 したがって、体心立方構造の配位数は4 + 4 = 8

面心立方構造 (fcc):

構造から、ユニットセルの8隅に8個の粒子があることがわかる。 各コーナー粒子は隣接する他の8つの単位セルに共有されている。 したがって、各単位セルにはその角の粒子の1/8が含まれる。 したがって、単位セルの角の粒子の数 = 1/8 x 8 = 1
単位セルの6つの面には6個の粒子がある。 各面の粒子は隣り合う2つのユニットセルで共有される。 したがって、各単位セルにはその面の粒子の1/2が含まれる。
面の数=6なので、面の粒子の数=1/2×6=3
したがって単位セルの粒子の数1+3=4
この構造中の各粒子はその層中の他の4粒子、上の層の4粒子、下の層の4粒子と直接接触していることになる。 したがって面心立方構造の配位数は4+4+4=12

注:
端面心粒子では4つのユニットセルで共有されます。 単位セルあたりの原子数は、化合物の化学量論と同じ比率である。 したがって、化合物の化学式を予測するのに役立つ。
理学 > 化学 > 固体 > ブラベ格子
のページです。