Unde se află centrul unui triunghi?
Există de fapt mii de centre!
Iată care sunt cele mai populare 4:
Centroid, Circumcenter, Incentru și Ortocentru
Pentru fiecare dintre acestea, „centrul” este acolo unde se intersectează linii speciale, deci totul depinde de aceste linii!
Să ne uităm la fiecare dintre ele:
Centroid
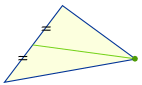 |
Desenați o linie (numită „mediană”) de la fiecare colț până la punctul median al laturii opuse. |
Încercați acest lucru: tăiați un triunghi din carton, desenați medianele. Se întâlnesc toate într-un punct? Puteți echilibra triunghiul în acel punct?
Centrul Circumcentru
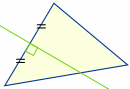 |
Desenați o linie (numită „bisectoare perpendiculară”) în unghi drept pe mijlocul fiecărei laturi. Unde se intersectează toate cele trei linii este centrul „circumferinței” unui triunghi, numit „circumcentru”: |
Încercați acest lucru: trageți punctele de mai sus până când obțineți un triunghi dreptunghic (doar cu ochiul liber este OK). Unde se află circumcentrul? De ce?
Centrul
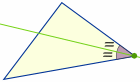 |
Desenați o linie (numită „bisectoarea unghiului”) dintr-un colț astfel încât să împartă unghiul în două Locul în care se intersectează toate cele trei linii este centrul „circumferinței” unui triunghi, numit „incentru”: |
Încercați acest lucru: găsiți incinta unui triunghi folosind un compas și o rigla la: Înscrierea unui cerc într-un triunghi
Ortocentrul
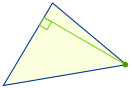 |
Desenați un segment de dreaptă (numit „altitudine”) în unghi drept cu o latură care merge spre colțul opus.Unde se intersectează toate cele trei linii este „ortocentrul”: |
Rețineți că uneori marginile triunghiului trebuie extinse în afara triunghiului pentru a desena altitudinile. Atunci, ortocentrul este, de asemenea, în afara triunghiului.
.

