Bravais Lattices

Vetenskap >Kemi >Fasta tillstånd >Bravais Lattices

I den här artikeln kommer vi att studera strukturerna hos Bravais Lattices.

En kristall är en homogen del av ett fast ämne som består av ett regelbundet mönster av strukturella enheter som är bundna genom plana ytor som gör en bestämd vinkel med varandra.

Enhetscell:

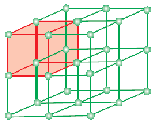
Enhetscellen är den minsta strukturella upprepningsenheten i ett kristallint fast ämne (rymdgitter). När enhetsceller av samma kristallina ämne upprepas i rummet i alla riktningar bildas ett kristallint fast ämne. Enhetscellen representeras på papper genom att man drar linjer som förbinder de ingående partiklarnas centra.

Den geometriska form som endast består av en regelbunden uppsättning punkter i rymden kallas gitter eller rymdgitter. Det kan definieras som en uppsättning punkter som visar hur molekyler, atomer eller joner är arrangerade på olika platser i ett tredimensionellt rum. Varje punkt i skärningspunkten mellan linjerna i enhetscellen representerar en beståndsdel, dvs. en molekyl, atom eller jon. Denna punkt där linjerna korsar varandra i enhetscellen kallas gitterpunkt eller gitterplats.

Anmärkning: Varje gitterpunkt i kristallgitteret har samma omgivning eller miljö. Två eller flera kristallina ämnen kan ha samma gitterplats. Varje enskild partikel i matrisen representeras alltid av en gitterpunkt i den tredimensionella matrisen.

Kristallgitterets egenskaper:

• Kristallgitteret är ett regelbundet arrangemang av beståndsdelarna i ett kristallint fast ämne i ett tredimensionellt rum.
• Det består av ett stort antal enhetsceller.
• Kristallgitteret definieras i termer av enhetscellens egenskaper.
• När det bryts upp bildar det många enhetsceller.
• Ett kristallgitter kan erhållas, hanteras och studeras i ett laboratorium under experiment.
• Det är en makroskopisk egenskap.

Kännetecken för enhetscell:

• En enhetscell är den minsta strukturella upprepande enheten i kristallina fasta ämnen.
• Det är den grundläggande enheten i kristallgitteret som har alla egenskaper hos kristallen.
• Enhetscellen definierar de grundläggande egenskaperna hos kristallgitteret.
• Enhetsceller är en grundläggande enhet och kan därför inte delas upp ytterligare.
• Enhetscellen är ett hypotetiskt begrepp och kan därför inte erhållas vid experiment.
• Det är en mikroskopisk egenskap.

Typer av rymdgitter:

Ettdimensionellt gitter:

I detta gitter existerar en uppsättning punkter som är arrangerade på lika avstånd längs.

Två dimensionellt lattice:

I denna typ finns två sidor och vinkeln mellan dem specificerad. Det finns fem typer av tvådimensionella gitter.

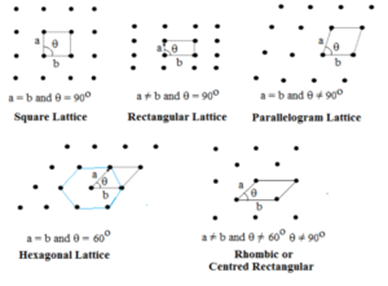
Hexagonalt gitter är en romb med θ = 60°

Bravaisgitter:

Låt längderna på de tre kanterna av enhetscellen vara a, b och c. Låt α vara vinkeln mellan sidorna b och c. Låt β vara vinkeln mellan sidorna a och c. Låt γ vara vinkeln mellan sidorna a och b.

Den franske matematikern Bravais sade att för olika värden på a, b, c och α, β, γ är högst fjorton (14) strukturer möjliga. Dessa arrangemang kallas Bravais Lattices.

14 Bravais Lattices:

.

.

Sr. Nr.	Kristall System	Rymdgitter Typ	Diagram	Kantlängder	Anglar	Exempel
	Kubisk	Enkel primitiv		a = b = c	α = β = γ = 90°	Polonium (Po)
	Kubisk	Kropp centrerad		a = b = c	α = β = γ = 90°	Iron (Fe), Rubidium (Rb), Natrium (Na), Titan (Ti), Vungsten (W), Uran (U), Zirkonium (Zr)
	Kubisk	Förhållning centrerad		a = b = c	α = β = γ = 90°	Koppar (Cu), Aluminium (Al), Nickel (Ni), Guld (Au), Silver (Ag), Platina (Pt)
	Tetragonalt	Enkel . primitive		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonal	Kropp centrerad		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombisk	Enkel primitive		a ≠ b ≠ c	α = β = γ = 90°	Rombiskt svavel
	Orthorhombiskt	Kropp centrerad		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombisk	Fasad centrerad		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Orthorhombisk	Endcentrerat slut		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monoklin	enkel primitive		a ≠ b ≠ c	α =γ = 90° och β ≠ 90°	Monoklin svavel
	Monoklin	Ett centrerat slut		a ≠ b ≠ c	α =γ = 90° och β ≠ 90	Na2SO4. 10H2O
	Triklinisk	Enkel primitive		a ≠ b ≠ c	α =γ = 90° och β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonal	Enkel primitive		a = b ≠ c	α = β = 90° och γ = 120°	ZnO, BeO, CoS, SnS
	Romboeder	Enkel primitive		a ≠ b ≠ c	α = β = γ ≠ 90°	Calcit, NaNO3, FeCO3

Partikel i hörnet:

Partikeln i hörnet av enhetscellen delas av 8 enhetsceller (4 lager under och 4 lager över). Därför har varje enhetscell 1/8 partikel.

Partikel på ytan:

Partikeln på ytan av enhetscellen delas av 2 intilliggande enhetsceller. Därför är varje enhetscell 1/2 partikel.

Partikel vid kanten:

Partikeln vid kanten av enhetscellen delas av 4 enhetsceller (2 lager under och 2 lager över). Därför är varje enhetscell 1/4 partikel.

Koordinationstal:

Koordinationstalet för den ingående partikeln i kristallgitteret är antalet partiklar som omger en enskild partikel i ett kristallgitter.

Jo högre koordinationstal desto tätare är partiklarna packade i kristallgitteret. Koordineringstalet är ett mått på kristallens hårdhet.

Antal partiklar i enhetscellen och koordineringstal

Simple Cubic Structure (scc):

Från strukturen kan vi se att det finns 8 partiklar i 8 hörn av enhetscellen.Varje hörnpartikel delas av 8 angränsande enhetsceller. Därför innehåller varje enhetscell 1/8 av partikeln i dess hörn.
Antal hörn = 8, därför är antalet partiklar i enhetscellen = 1/8x 8 = 1

Varje partikel i denna struktur är i direkt kontakt med fyra andra partiklar i dess plan och en partikel vardera i skiktet ovanför och i skiktet nedanför. Hencethe koordinationstal för enkel kubisk struktur är 4+ 1+ 1 = 6

Kroppscentrerad kubisk struktur (bcc):

Från strukturen kan vi se att det finns 8 partiklar i 8 hörn av enhetscellen.Varje hörnpartikel delas av 8 angränsande enhetsceller. Därför innehåller varje enhetscell 1/8 av partikeln i sitt hörn. Antal hörn = 8, därför är antalet partiklar i enhetscellen vid hörnen = 1/8 x 8 = 1

Tidigare finns det en atom i cellens centrum, därför är antalet partiklar i enhetscellen 1 + 1 = 2

Varje partikel i denna struktur står i direkt kontakt med fyra andra partiklar i lagret ovanför och fyra partiklar i lagret under. Därför är koordinationstalet för kroppscentrerad kubisk struktur 4 + 4 = 8

FaceCentered Cubic Structure (fcc):

Uppifrån strukturen ser vi att det finns 8 partiklar vid 8 hörn i enhetscellen. Varje hörnpartikel delas av 8 andra angränsande enhetsceller. Därför innehåller varje enhetscell 1/8 av partikeln i dess hörn. Antalet hörn är 8. Därför är antalet partiklar i en enhetscell vid hörnen = 1/8 x 8 = 1

Det finns 6partiklar vid 6 sidor av enhetscellen. Varje partikel på varje sida delas av två angränsande enhetsceller. Därför innehåller varje enhetscell 1/2 av partikeln på dess yta.
Antalet ytor = 6. Därför är antalet partiklar på ytan = 1/2 x 6 = 3

Det innebär att antalet partiklar i enhetscellen är 1 + 3 = 4

Varje partikel i denna struktur är i direkt kontakt med 4 andra partiklar i sitt lager och med 4 partiklar i lagret ovanför och 4 partiklar i lagret nedanför. Därför är koordinationstalet för den kantcentrerade kubiska strukturen 4 + 4 + 4 = 12

Anmärkningar:

För den kantcentrerade partikeln är den delad med 4 enhetsceller. Varje enhetscell består alltså av 1/4 partikel. Antalet atomer per enhetscell är i samma förhållande som föreningens stökiometri. Därför hjälper det till att förutsäga föreningens formel.

Naturvetenskap > Kemi > Fast tillstånd > Bravais-gitter