Věda > Chemie > Pevné látky > Bravaisovy mřížky
V tomto článku se budeme zabývat strukturami Bravaisových mřížek.
Krystal je homogenní část pevné látky tvořená pravidelným uspořádáním strukturních jednotek spojených rovinnými plochami svírajícími mezi sebou určitý úhel.
Jednotková buňka:
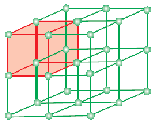
Jednotková buňka je nejmenší strukturní opakující se jednotka krystalické pevné látky (prostorová mřížka). Když se jednotkové buňky téže krystalické látky opakují v prostoru ve všech směrech, vzniká krystalická pevná látka. Jednotková buňka se na papíře znázorňuje nakreslením čar spojujících středy jednotlivých částic.
Geometrická forma sestávající pouze z pravidelného uspořádání bodů v prostoru se nazývá mřížka nebo prostorová mřížka. Lze ji definovat jako pole bodůzobrazující, jak jsou molekuly, atomy nebo ionty uspořádány na různých místech, v trojrozměrném prostoru. Každý bod na průsečíku čar vjednotlivé buňce představuje složenou částici, tj. molekulu nebo atom nebo iont. Tento bod průsečíku čar v jednotkové buňce se nazývá mřížkový bod nebo mřížkové místo.
Poznámka: Každý mřížkový bod v krystalové mřížce má stejné okolí nebo prostředí. Dvě nebo více krystalických látek mohou mítstejné mřížkové místo. Každá částice v mřížce je vždy reprezentována mřížkovým bodem v trojrozměrném poli.
Charakteristika krystalové mřížky:
- Krystalová mřížka je pravidelné uspořádání základních částic krystalické látky v trojrozměrném prostoru.
- Skládá se z velkého počtu jednotkových buněk.
- Krystalová mřížka je definována z hlediska vlastností jednotkové buňky.
- Při rozpadu tvoří četné jednotkové buňky.
- Krystalovou mřížku lze získat, zpracovat a studovat v laboratoři při experimentech.
- Je to makroskopická vlastnost.
Charakteristika jednotkové buňky:
- Jednotková buňka je nejmenší strukturní opakující se jednotka krystalické pevné látky.
- Jedná se o základní jednotku krystalové mřížky, která má všechny vlastnosti krystalu.
- Jednotková buňka definuje základní vlastnosti krystalové mřížky.
- Jednotková buňka je základní jednotkou, proto ji nelze dále dělit.
- Jednotková buňka je hypotetický pojem Proto ji nelze získat při experimentech.
- Je to mikroskopická vlastnost.
Typy prostorových mřížek:
Jednorozměrná mřížka:
V této mřížce existuje množina bodů uspořádaných ve stejných vzdálenostech podél.

Dvourozměrná mřížka:
V tomto typu jsou určeny dvě strany a úhel mezi nimi. Existuje pět typů dvourozměrných mříží.
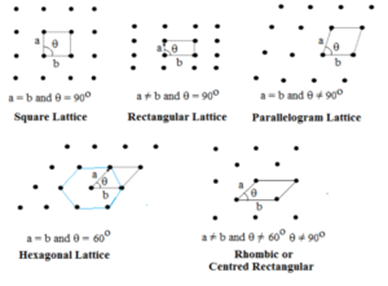
Šestihranná mřížka je kosočtverec s θ = 60°
Bravaisova mřížka:

Nechť délky tří hran jednotkové buňky jsou a, b a c. Nechť α je úhel mezi stranami b a c. Nechť β je úhel mezi stranami a a c. Nechť γ je úhel mezi stranami a a b.
Francouzský matematik Bravais řekl, že pro různé hodnoty a, b, c a α, β, γ je možných maximálně čtrnáct (14) struktur. Tato uspořádání se nazývají Bravaisovy mřížky.
14 Bravaisových mřížek:
|
Sr. Č. |
Krystal Systém |
Prostor mřížky Typ |
Diagram |
Délky hran |
Úhelník |
Příklady |
|
Kubický |
Prostý primitivní |
 |
a = b = c |
α = β = γ = 90° |
Polonium (Po) |
|
|
Kubický |
Těleso centrované |
 |
a = b = c |
α = β = γ = 90° |
Železo (Fe), Rubidium (Rb), Sodík (Na), Titan (Ti), Volfram (W), Uran (U), Zirkonium (Zr) |
|
|
Kubický |
Čelně centrovaný |
 |
a = b = c |
α = β = γ = 90° |
Měď (Cu), Hliník (Al), Nikl (Ni), Zlato (Au), Stříbro (Ag), Platina (Pt) |
|
|
Tetragonální |
Prostý primitivní |
 |
a = b ≠ c |
α = β = γ = 90° |
SnO2 |
|
|
Tetragonální |
Těleso centrované |
 |
a = b ≠ c |
α = β = γ = 90° |
Ti, O2, CaSO4 |
|
|
Orthorhombický |
Jednoduchý primitivní |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
Rombická síra |
|
|
Ortorhombická |
Těleso centrované |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
KNO3 |
|
|
Orthorhombický |
Tvář. centrovaný |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
BaSO4 |
|
|
Orthorhombický |
Konec centrovaný |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
MgSO4, 7H2O |
|
|
monoklinický |
jednoduchý primitivní |
 |
a ≠ b ≠ c |
α =γ = 90° a β ≠ 90° |
Monoklinická síra |
|
|
Monoklinická |
Konec centrovaný |
 |
a ≠ b ≠ c |
α =γ = 90° a β ≠ 90 |
Na2SO4. 10H2O |
|
|
Triklinický |
jednoduchý primitivní |
 |
a ≠ b ≠ c |
α =γ = 90° a β ≠ 90° |
K2Cr2O7, H3BO3 |
|
|
šestihranný |
jednoduchý primitivní |
 |
a = b ≠ c |
α = β = 90° a γ = 120° |
ZnO, BeO, CoS, SnS |
|
|
Rhombohedral |
Simple primitivní |
 |
a ≠ b ≠ c |
α = β = γ ≠ 90° |
Kalcit, NaNO3, FeCO3 |
Částice v rohu:

Částicev rohu jednotkové buňky je společná pro 8 jednotkových buněk (4 vrstvy pod a 4 vrstvy nad). Proto každá jednotková buňka 1/8 částice.
Částice na čelní straně:

Částicena čelní straně jednotkové buňky je sdílena 2 sousedními jednotkovými buňkami. Protokaždá jednotková buňka 1/2 částice.
Částice na okraji:

Částicena okraji jednotkové buňky je sdílena 4 jednotkovými buňkami (2 vrstvy pod a2 vrstvy nad). Každá jednotková buňka tedy 1/4 částice.
Koordinační číslo:
Koordinační číslo částice tvořící krystalovou mřížku je pak počet částic obklopujících jednu částici v krystalové mřížce.
Větší koordinační číslo je těsněji zabalené částice v krystalové mřížce. Koordinační číslo je měřítkem tvrdosti krystalu.
Počet částic v jednotkové buňce a koordinační číslo
Prostá kubická struktura (scc):

Ze struktury vidíme, že v 8 rozích jednotkové buňky je 8 částic. každá rohová částice je společná pro 8 sousedních jednotkových buněk. Každá jednotková buňka tedy obsahuje 1/8 částice ve svém rohu.
Počet rohů = 8, tedy počet částic v jednotkové buňce = 1/8x 8 = 1
Každá částice v této struktuře je v přímém kontaktu se čtyřmi dalšími částicemi ve své rovině a po jedné částici ve vrstvě nad a pod ní. Hencetovo koordinační číslo pro jednoduchou kubickou strukturu je 4+ 1+ 1 = 6

Kubická struktura s tělesným středem (bcc):

Z této struktury vidíme, že v 8 rozích jednotkové buňky je 8 částic.Každá rohová částice je společná pro 8 sousedních jednotkových buněk. Každá jednotková buňka tedy obsahuje 1/8 částice ve svém rohu. Počet rohů = 8,tudíž počet částic v jednotkové buňce v rozích = 1/8 x 8 = 1
Ve středu buňky je zároveň atom, tudíž počet částic v jednotkové buňce 1 + 1 = 2
Každá částice v této struktuře je v přímém kontaktu se čtyřmi dalšími částicemi ve vrstvě nad ní a čtyřmi částicemi ve vrstvě pod ní. Koordinační číslo pro tělesově centrovanou kubickou strukturu je tedy 4 + 4 = 8

Tělesově centrovaná kubická struktura (fcc):

Z této struktury vidíme, že v 8 rozích jednotkové buňky je 8 částic. Každá rohová částice je společná pro 8 dalších sousedních jednotkových buněk. Každá jednotková buňka tedy obsahuje 1/8 částice ve svém rohu. Počet rohů = 8. Proto počet částic v jednotkové buňce v rozích = 1/8 x 8 = 1
Na 6 stěnách jednotkové buňky je 6částic. Každá částice na stěně je společná pro 2sousední jednotkové buňky. Proto každá jednotková buňka obsahuje 1/2 částic na své stěně.
Počet stěn = 6. Proto počet částic na stěně = 1/2 x 6 = 3
Tudíž počet částic v jednotkové buňce 1 + 3 = 4
Každá částice v této struktuře je v přímém kontaktu se 4 dalšími částicemi ve své vrstvě a se 4 částicemi ve vrstvě nad a4 částicemi ve vrstvě pod. Koordinační číslo pro krychlovou strukturu s hranovým centrováním je tedy 4 + 4 + 4 = 12

Poznámky:
Pro částice s hranovým centrováním je sdíleno 4 jednotkovými buňkami. Každou jednotkovou buňku tedy tvoří 1/4 částice Počet atomů na jednotkovou buňku je ve stejném poměru jako stechiometrie sloučeniny. Proto pomáhá předpovědět vzorec sloučeniny.
Věda > Chemie > Pevné látky > Bravaisovy mřížky