Bravais Lattices

Tiede >Kemia > Kiinteä olomuoto > Bravais Lattices

Tässä artikkelissa tutkitaan Bravais Lattices -rakenteita.

Kide on kiinteän aineen homogeeninen osa, joka koostuu säännönmukaisesta rakenteellisten yksiköiden kuviosta, jotka on sidottu toisiinsa tasopinnoilla, jotka muodostavat tietyn kulman toisiinsa nähden.

Yksikkösolu:

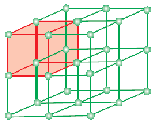
Yksikkösolu on kiteisen kiintoaineen rakenteellinen toistuva yksikkö (avaruusristikko). Kun saman kiteisen aineen yksikkösolut toistuvat avaruudessa kaikissa suunnissa, muodostuu kiteinen kiinteä aine. Yksikkösolu esitetään paperilla piirtämällä hiukkasten keskipisteet yhdistäviä viivoja.

Geometrista muotoa, joka koostuu vain säännöllisestä pistemäärästä avaruudessa, kutsutaan ristikoksi tai avaruusristikoksi. Se voidaan määritellä pistejoukoksi, joka osoittaa, miten molekyylit, atomit tai ionit on järjestetty eri paikkoihin kolmiulotteisessa avaruudessa. Jokainen piste yksikkösolun viivojen leikkauspisteessä edustaa hiukkasta eli molekyyliä, atomia tai ionia. Tätä yksikkösolun viivojen leikkauspistettä kutsutaan ristikkopisteeksi tai ristikkopaikaksi.

Huomautus: Kristalliristikon jokaisella ristikkopisteellä on samanlainenympäristö tai ympäristö. Kahdella tai useammalla kiteisellä aineella voi olla sama ristikkotila. Jokainen hiukkanen edustaa aina kolmiulotteisen joukon ristikkopistettä.

Kristalliristikon ominaisuudet:

• Kristalliristikko on kiteisen kiinteän aineen muodostavien hiukkasten säännöllinen järjestys kolmiulotteisessa avaruudessa.
• Se koostuu suuresta määrästä yksikkösoluja.
• Kideverkko määritellään yksikkösolun ominaisuuksien perusteella.
• Kideverkko muodostaa hajotessaan lukuisia yksikkösoluja.
• Kideverkkoa voidaan saada, käsitellä ja tutkia laboratoriossa kokeissa.
• Se on makroskooppinen ominaisuus.

Yksikkösolun ominaisuudet:

• Yksikkösolu on kiteisen kiinteän aineen pienin rakenteellinen toistuva yksikkö.
• Se on kideruudukon perusyksikkö, jolla on kaikki kiteen ominaisuudet.
• Yksikkösolu määrittelee kideruudukon perusominaisuudet.
• Yksikkösolu on perusyksikkö, joten sitä ei voida jakaa enempää.
• Yksikkösolu on hypoteettinen käsite Näin ollen sitä ei voida saada kokeissa.
• Se on mikroskooppinen ominaisuus.

Avaruusristikon tyypit:

Yksiulotteinen ristikko:

Tässä ristikossa on olemassa joukko pisteitä, jotka on järjestetty yhtäläisillä etäisyyksillä pitkin.

Kaksiulotteinen ristikko:

Tässä tyypissä on määritelty kaksi sivua ja niiden välinen kulma. Kaksiulotteisia ristikkoja on viittä tyyppiä.

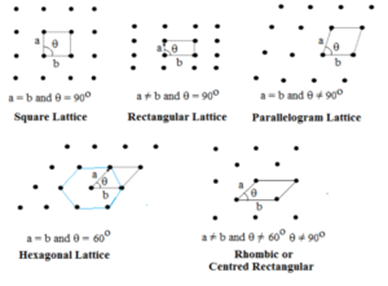
Hexagonaalinen ristikko on rombi, jonka θ = 60°

Bravais’n ristikko:

Letetään, että yksikkösolun kolmen reunan pituudet ovat a, b ja c. Olkoon α sivujen b ja c välinen kulma. Olkoon β sivujen a ja c välinen kulma. Olkoon γ sivujen a ja b välinen kulma.

Ranskalainen matemaatikko Bravais sanoi, että eri a-, b-, c- ja α-, β-, γ-arvoilla on korkeintaan neljätoista (14) rakennetta mahdollista. Näitä järjestelyjä kutsutaan Bravais’n ristikoiksi.

14 Bravais’n ristikkoa:

.

SnO2

.

.

.

Sr. Nro.	Kristalli Systeemi	Avaruusristikko Tyyppi	Diagrammi	Särmien pituudet	Kulmat	Esimerkkejä
	Kuutio	Simple primitiivinen		a = b = c	α = β = γ = 90°	Polonium (Po)
	Kuutio	Kappaleen keskipiste		a = b = c	α = β = γ = 90°	Rauta (Fe), Rubidium (Rb), Natrium (Na), Titaani (Ti), Volframi (W), Uraani (U), Zirkonium (Zr)
	Kuutio	Pinta keskitetty		a = b = c	α = β = γ = 90°	Kupari (Cu), Alumiini (Al), Nikkeli (Ni), Kulta (Au), Hopea (Ag), Platina (Pt)
	Tetragonaalinen	Yksinkertainen . primitiivinen		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonaalinen	Runko. keskitetty		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombinen	Simple primitiivinen		a ≠ b ≠ c	α = β = γ = 90°	Rhombinen rikki
	Orthorhombinen	Keho keskitetty		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombinen	Face keskitetty		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Orthorhombinen	Pää keskitetty		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monokliininen	simple primitiivinen		a ≠ b ≠ c	α =γ = 90° ja β ≠ 90°	Monokliininen rikki
	Monokliininen	Pää keskitetty		a ≠ b ≠ c	α =γ = 90° ja β ≠ 90	Na2SO4. 10H2O
	trikliininen	yksinkertainen alkuinen		a ≠ b ≠ c	α =γ = 90° ja β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonal	Simple primitiivinen		a = b ≠ c	α = β = 90° ja γ = 120°	ZnO, BeO, CoS, SnS
	Rhombohedral	Simple primitive		a ≠ b ≠ c	α = β = γ ≠ 90°	Kalsiitti, NaNO3, FeCO3

Hiukkanen kulmassa:

Yksikkösolun kulmassa oleva hiukkanen on jaettu 8 yksikkösolun kesken (4 kerrosta alapuolella ja 4 kerrosta yläpuolella). Näin ollen jokainen yksikkösolu 1/8 hiukkasta.

Hiukkanen otsalla:

Yksikkösolun otsalla olevan hiukkasen jakavat 2 vierekkäistä yksikkösolua. Sitenjokainen yksikkösolu 1/2 hiukkasta.

Hiukkanen reunalla:

Yksikkösolun reunalla olevan hiukkasen jakavat 4 yksikkösolua (2 kerrosta alapuolella ja2 kerrosta yläpuolella). Näin ollen kukin yksikkösolu 1/4 hiukkasta.

Koordinaatioluku:

Kideverkon muodostavan hiukkasen koordinaatioluku onkristalliristikon yksittäistä hiukkasta ympäröivien hiukkasten lukumäärä.

Mitä suurempi koordinaatioluku, sitä tiiviimmin hiukkaset ovat pakkautuneet kideverkkoon. Koordinaatioluku on kiteen kovuuden mittari.

Yksikkösolun hiukkasten lukumäärä ja koordinaatioluku

Simple Cubic Structure (scc):

Rakenteesta nähdään, että yksikkösolun kahdeksassa kulmassa on kahdeksan hiukkasta.Kukin kulmahiukkanen jakautuu kahdeksaan viereiseen yksikkösoluun. Näin ollen kukin yksikkösolu sisältää 1/8 sen kulmassa olevasta hiukkasesta.
Nurkkien lukumäärä = 8, Näin ollen hiukkasten lukumäärä yksikkösolussa = 1/8x 8 = 1

Jokainen hiukkanen tässä rakenteessa on suorassa kosketuksessa neljään muuhun hiukkaseen sen tasossa ja kumpaankin hiukkaseen sen yläpuolella ja alapuolella olevassa kerroksessa. Hencethe koordinaatioluku yksinkertaiselle kuutiorakenteelle on 4+ 1+ 1 = 6

Kappaleenkeskeinen kuutiorakenne (bcc):

Rakenteesta nähdään, että yksikkösolun kahdeksassa kulmassa on kahdeksan hiukkasta.Jokainen kulmahiukkanen on jaettu 8 viereisen yksikkösolun kanssa. Näin ollen kukin yksikkösolu sisältää 1/8 th sen kulmassa olevasta hiukkasesta. Kulmien lukumäärä = 8,joten hiukkasten lukumäärä yksikkösolussa kulmissa = 1/8 x 8 = 1

Yksikkösolun keskellä on samaan aikaan atomi, joten hiukkasten lukumäärä yksikkösolussa 1 + 1 = 2

Jokainen hiukkanen tässä rakenteessa on suorassa kosketuksessa neljään muuhun hiukkaseen yläpuolisessa kerroksessa ja neljään hiukkaseen alapuolisessa kerroksessa. Näin ollen koordinaatioluku kappalekeskeisessä kuutiorakenteessa on 4 + 4 = 8

Kappalekeskeinen kuutiorakenne (fcc):

Rakenteesta nähdään, että yksikkösolun kahdeksassa kulmassa on kahdeksan hiukkasta. Jokainen kulmahiukkanen on jaettu 8 muun viereisen yksikkösolun kanssa. Näin ollen jokainen yksikkösolu sisältää 1/8 th hiukkasta kulmassaan. Kulmien lukumäärä = 8. Näin ollen yksikkösolun hiukkasten lukumäärä kulmissa = 1/8 x 8 = 1

Yksikkösolun 6 pinnalla on 6 hiukkasta. Kukin kasvojen hiukkanen on jaettu 2naapurien yksikkösolujen kanssa. Näin ollen kussakin yksikkösolussa on 1/2 hiukkasta sen pinnalla.
Pintojen lukumäärä = 6. Näin ollen hiukkasten lukumäärä pinnalla = 1/2 x 6 = 3

Siten hiukkasten lukumäärä yksikkösolussa 1 + 3 = 4

Jokainen hiukkanen tässä rakenteessa on suorassa kosketuksessa 4:n muun hiukkasen kanssa kerroksessaan ja 4:n yläpuolella olevan kerroksen hiukkasen ja 4:n alapuolella olevan kerroksen hiukkasen kanssa. Näin ollen reunakeskisen kuutiorakenteen koordinaatioluku on 4 + 4 + 4 = 12

Huomautuksia:

Reunakeskisellä hiukkasella se on jaettu 4 yksikkösolun kesken. Näin ollen jokainen yksikkösolu koostuu 1/4 hiukkasesta Atomien lukumäärä yksikkösolua kohti on samassa suhteessa kuin yhdisteen stoikiometria. Näin ollen se auttaa ennustamaan yhdisteen kaavan.

Tiede > Kemia > Kiinteä olomuoto > Bravais’n hilat