Rețele Bravais

Știință > Chimie > Stare solidă > Rețele Bravais

În acest articol, vom studia structurile rețelelor Bravais.

Un cristal este o porțiune omogenă a unei substanțe solide alcătuită dintr-un model regulat de unități structurale legate prin suprafețe plane care fac un unghi definit între ele.

Celula unitară:

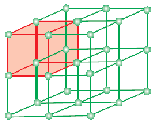
O celulă unitară este cea mai mică unitate structurală repetitivă a unui solid cristalin (rețeaua spațială). Atunci când celulele unitare ale aceleiași substanțe cristaline se repetă în spațiu în toate direcțiile, se formează un solid cristalin. Celula unitară este reprezentată pe hârtie prin trasarea unor linii care leagă centrele particulelor constitutive.

Forma geometrică formată numai dintr-o serie regulată de puncte în spațiu se numește rețea sau zăbrele spațială. Ea poate fi definită ca o matrice de puncte care arată modul în care sunt dispuse moleculele, atomii sau ionii în diferite locuri, într-un spațiu tridimensional. Fiecare punct de la intersecția liniilor din celula unitară reprezintă o particulă constitutivă, respectiv o moleculă, un atom sau un ion. Acest punct de intersecție a liniilor din celula unitară se numește punct de rețea sau site de rețea.

Nota: Fiecare punct de rețea din rețeaua cristalină are același înconjur sau mediu. Două sau mai multe substanțe cristaline pot avea același spațiu reticular. Fiecare particulă din rețea este întotdeauna reprezentată de un punct de rețea în rețeaua tridimensională.

Caracteristicile rețelei cristaline:

• Rețeaua cristalină este un aranjament regulat al particulelor constitutive ale unui solid cristalin în spațiul tridimensional.
• Este formată dintr-un număr mare de celule unitare.
• Rețeaua cristalină este definită în termeni de proprietăți ale celulei unitare.
• La descompunere, formează numeroase celule unitare.
• O rețea cristalină poate fi obținută, manipulată și studiată în laborator în timpul experimentelor.
• Este o proprietate macroscopică.

Caracteristicile celulei unitare:

• O celulă unitară este cea mai mică unitate structurală repetitivă a unui solid cristalin.
• Este unitatea fundamentală a rețelei cristaline care posedă toate proprietățile cristalului.
• Celula unitară definește proprietățile fundamentale ale rețelei cristaline.
• Celulele unitare sunt o unitate fundamentală, prin urmare nu pot fi divizate mai departe.
• O celulă unitară este un concept ipotetic Prin urmare, nu poate fi obținută în timpul experimentelor.
• Este o proprietate microscopică.

Tipuri de rețele spațiale:

Rețea unidimensională:

În această rețea, există un set de puncte dispuse la distanțe egale de-a lungul.

Rețea bidimensională:

În acest tip, se specifică două laturi și unghiul dintre ele. Există cinci tipuri de rețele bidimensionale.

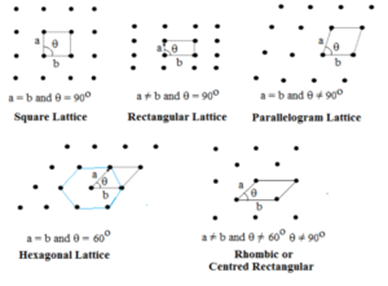
Rețeaua hexagonală este un romb cu θ = 60°

Rețelele Bravais:

Să fie lungimile celor trei muchii ale celulei unitare a, b și c. Fie α unghiul dintre laturile b și c. Fie β unghiul dintre laturile a și c. Fie γ unghiul dintre laturile a și b.

Matematicianul francez Bravais a spus că pentru diferite valori ale lui a, b, c și α, β, γ, sunt posibile maximum paisprezece (14) structuri. Aceste structuri se numesc rețele Bravais.

14 Rețele Bravais:

.

.

.

.

.

.

.

.

Sr. Nr.	Cristal Sistem	Rețea spațială Tip	Diagramă	Lungimi de muchie	Anguli	Exemple
	Cubic	Simplu primitiv .		a = b = c	α = β = γ = 90°	Polonium (Po)
	Cubic	Corp centrat		a = b = c	α = β = γ = 90°	Iron (Fe), Rubidiu (Rb), Sodiu (Na), Titaniu (Ti), Tungsten (W), Uraniu (U), Zirconiu (Zr)
	Cubic	Față centrată		a = b = c	α = β = γ = 90°	Cupru (Cu), Aluminiu (Al), Nichel (Ni), Our (Au), Argint (Ag), Platina (Pt)
	Tetragonal	Simplu . primitiv		a = b ≠ c	α = β = γ = 90° .	SnO2
	Tetragonal	Corpul centrat		a = b ≠ c	α = β = γ = 90°		Ti, O2, CaSO4
	Orthorhombic	Simplu . primitive		a ≠ b ≠ c	α = β = γ = 90°	.	Sulfură rombică
	Sulfură ortorombică	Corpul centrat		a ≠ b ≠ c	α = β = γ = 90°	.	KNO3
	Orthorhombic	Față centrat		a ≠ b ≠ c	α = β = γ = 90°	.	BaSO4
	Orthorhombic	Final centrat		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monoclinic	simplu . primitiv		a ≠ b ≠ c	α =γ = 90° și β ≠ 90°	Sulfură monoclinică
	Monoclinică	Extremitate centrată		a ≠ b ≠ c	α =γ = 90° și β ≠ 90		Na2SO4. 10H2O
	Triclinic	simplu primitiv		a ≠ b ≠ c	α =γ = 90° și β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonal	Simplu primitiv		a = b ≠ c	α = β = 90° și γ = 120°	ZnO, BeO, CoS, SnS
	Rhomboedru	Simplu primitiv .		a ≠ b ≠ c	α = β = γ ≠ 90°	Calcite, NaNO3, FeCO3

Particulă la colț:

Particula din colțul celulei unitare este împărțită de 8 celule unitare (4 straturi dedesubt și 4 straturi de deasupra). Prin urmare, fiecare celulă unitară 1/8 particulă.

Particulă la fața:

Particula de la fața celulei unitare este împărțită de 2 celule unitare adiacente. Prin urmare, fiecare celulă unitară 1/2 particulă.

Particulă la margine:

Particula de la marginea celulei unitare este împărțită de 4 celule unitare (2 straturi dedesubt și 2 straturi de deasupra). Prin urmare, fiecare celulă unitară are 1/4 particulă.

Numărul de coordonare:

Numărul de coordonare al particulei constitutive a rețelei cristaline este numărul de particule care înconjoară o singură particulă într-o rețea cristalină.

Cât mai mare este numărul de coordonare, mai strâns sunt împachetate particulele în rețeaua cristalină. Numărul de coordonare este măsura durității cristalului.

Numărul de particule din celula unitară și numărul de coordonare

Structura cubică simplă (scc):

Din această structură se poate observa că există 8 particule la 8 colțuri ale celulei unitare.Fiecare particulă din colț este împărțită de 8 celule unitare vecine. Prin urmare, fiecare celulă unitară conține 1/8 din particula de la colțul său.
Numărul de colțuri = 8, deci numărul de particule din celula unitară = 1/8x 8 = 1

Care particulă din această structură este în contact direct cu alte patru particule din planul său și cu câte o particulă din stratul superior și din stratul inferior. Hencetenumărul de coordinare pentru structura cubică simplă este 4+ 1+ 1 = 6

Structura cubică centrată pe corp (bcc):

Din această structură se poate observa că există 8 particule în cele 8 colțuri ale celulei unitare.Fiecare particulă de colț este împărțită de 8 celule unitare învecinate. Prin urmare, fiecare celulă unitară conține 1/8 din particula din colțul său. Numărul de colțuri = 8, deci numărul de particule din celula unitară la colțuri = 1/8 x 8 = 1

În același timp, există un atom în centrul celulei, deci numărul de particule din celula unitară 1 + 1 = 2

Care particulă din această structură este în contact direct cu alte patru particule din stratul superior și patru particule din stratul inferior. Prin urmare, numărul de coordinație pentru structura cubică centrată pe corp este 4 + 4 = 8

Structura cubică centrată pe față (fcc):

Din structură, putem vedea că există 8 particule în 8 colțuri ale celulei unitare. Fiecare particulă de colț este împărțită cu alte 8 celule unitare vecine. Prin urmare, fiecare celulă unitară conține 1/8 din particula din colțul său. Numărul de colțuri = 8. Prin urmare, numărul de particule dintr-o celulă unitară la colțuri = 1/8 x 8 = 1

Există 6 particule la 6 fețe ale celulei unitare. Fiecare particulă de pe fiecare față este împărțită cu 2 celule unitare învecinate. Prin urmare, fiecare celulă unitară conține 1/2 din particula de pe fața sa.
Numărul de fețe = 6. Prin urmare, numărul de particule de pe față = 1/2 x 6 = 3

De aici numărul de particule din celula unitară 1 + 3 = 4

Care particulă din această structură este în contact direct cu alte 4 particule din stratul său și cu 4 particule din stratul superior și 4 particule din stratul inferior. Prin urmare, numărul de coordonare pentru structura cubică centrată pe față este 4 + 4 + 4 + 4 = 12

Note:

Pentru particula centrată pe muchie, aceasta este împărțită de 4 celule unitare. Prin urmare, fiecare celulă unitară este formată din 1/4 particulă Numărul de atomi pe celulă unitară este în același raport cu stoichiometria compusului. Prin urmare, ajută la prezicerea formulei compusului.

Știință > Chimie > Stare solidă > Rețele Bravais