Test for uafhængighed
Hypotesetest, som vi er stødt på tidligere i bogen, havde at gøre med, hvordan de numeriske værdier af to populationsparametre sammenlignes. I dette underafsnit vil vi undersøge hypoteser, der har at gøre med, om to tilfældige variabler tager deres værdier uafhængigt af hinanden eller ej, eller om værdien af den ene har en sammenhæng med værdien af den anden. Hypoteserne vil således blive udtrykt i ord og ikke i matematiske symboler. Vi bygger diskussionen op omkring følgende eksempel:
Der findes en teori om, at kønnet på en baby i livmoderen hænger sammen med babyens hjertefrekvens: babypiger har tendens til at have en højere hjertefrekvens. Lad os antage, at vi ønsker at teste denne teori. Vi undersøger 40 babyers hjerterytmeoptegnelser, der er taget i forbindelse med mødrenes sidste prænatale kontrol før fødslen, og for hver af disse 40 tilfældigt udvalgte optegnelser beregner vi værdierne af to tilfældige mål: 1) køn og 2) hjertefrekvens. I denne sammenhæng kaldes disse to tilfældige mål ofte faktorer En variabel med flere kvalitative niveauer… Da bevisbyrden er, at hjertefrekvens og køn hænger sammen, ikke at de ikke er uafhængige, kan problemet med at teste teorien om babyens køn og hjertefrekvens formuleres som en test af følgende hypoteser:
H0:Babyens køn og babyens hjertefrekvens er uafhængigevs. Ha:Babykøn og babyhjertefrekvens er ikke uafhængige
Faktoren køn har to naturlige kategorier eller niveauer: dreng og pige. Vi opdeler den anden faktor, hjerterytme, i to niveauer, lav og høj, ved at vælge en vis hjerterytme, f.eks. 145 slag pr. minut, som grænsen mellem dem. En puls under 145 slag pr. minut betragtes som lav og 145 slag pr. minut og derover som høj. De 40 registreringer giver anledning til en 2 × 2 kontingenstabel. Ved at lægge rækketotaler, kolonnetotaler og en samlet totalsum sammen får vi den tabel, der er vist som tabel 11.1 “Baby Gender and Heart Rate”. De fire poster med fed skrift er optællinger af observationer fra stikprøven på n = 40. Der var 11 piger med lav hjerterytme, 17 drenge med lav hjerterytme osv. De udgør kernen i den udvidede tabel.
Tabel 11.1 Babys køn og hjertefrekvens
| Hjertefrekvens | ||||
|---|---|---|---|---|
| Lavt | Højt | Række i alt | ||
| Genre | Pige | 11 | 7 | 18 |
| Dreng | 17 | 5 | 22 | |
| Spalte i alt | 28 | 12 | Total = 40 | |
I analogi med det faktum, at sandsynligheden for uafhængige hændelser er produktet af sandsynlighederne for hver enkelt hændelse, hvis hjertefrekvens og køn var uafhængige, ville vi forvente, at antallet i hver kernecelle ville være tæt på produktet af rækkens total R og kolonnens total C for den række og kolonne, der indeholder den, divideret med stikprøvens størrelse n. Hvis vi betegner et sådant forventet antal observationer E, er disse fire forventede værdier:
- 1. række og 1. kolonne: E=(R×C)∕n=18×28∕40=12,6
- 1. række og 2. kolonne: E=(R×C)∕n=18×28∕40=12,6
- 1: E=(R×C)∕n=18×12∕40=5,4
- 2. række og 1. kolonne: E=(R×C)∕n=18×12∕40=5,4
- 2: E=(R×C)∕n=22×28∕40=15,4
- 2. række og 2. kolonne: E=(R×C)∕n=22×28∕40=15,4
- 2: E=(R×C)∕n=22×12∕40=6,6
Vi opdaterer tabel 11.1 “Babykøn og hjertefrekvens” ved at placere hver forventet værdi i den tilsvarende kernecelle, lige under den observerede værdi i cellen. Dette giver den opdaterede tabel Tabel 11.2 “Opdateret babykøn og hjertefrekvens”.
Tabel 11.2 Opdateret Babys køn og hjertefrekvens
| Hjertefrekvens | ||||
|---|---|---|---|---|
| Lav | Høj | Række i alt | ||
| Genre | Pige | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Dreng | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Spalte i alt | C = 28 | C = 12 | n = 40 | |
Et mål for, hvor meget dataene afviger fra det, vi ville forvente at se, hvis faktorerne virkelig var uafhængige, er summen af kvadraterne af forskellen på tallene i hver kernecelle, eller, ved at standardisere ved at dividere hvert kvadrat med det forventede antal i cellen, summen Σ(O-E)2∕E. Vi ville kun forkaste nulhypotesen om, at faktorerne er uafhængige, hvis dette tal er stort, så testen er højresvinget. I dette eksempel har den tilfældige variabel Σ(O-E)2∕E chi-kvadratfordelingen med én frihedsgrad. Hvis vi fra starten havde besluttet at teste på 10 % signifikansniveau, ville den kritiske værdi, der definerer afvisningsområdet, ifølge figur 12.4 “Critical Values of Chi-Square Distributions” være χα2=χ0,102=2,706, således at afvisningsområdet ville være intervallet [2,706,∞). Når vi beregner værdien af den standardiserede teststatistik, får vi
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Da 1,231 < 2,706, er beslutningen ikke at forkaste H0. Se figur 11.3 “Forudsigelse af babyens køn”. Dataene giver ikke tilstrækkeligt bevis på 10 % signifikansniveau til at konkludere, at hjertefrekvens og køn hænger sammen.
Figur 11.3 Forudsigelse af babykøn
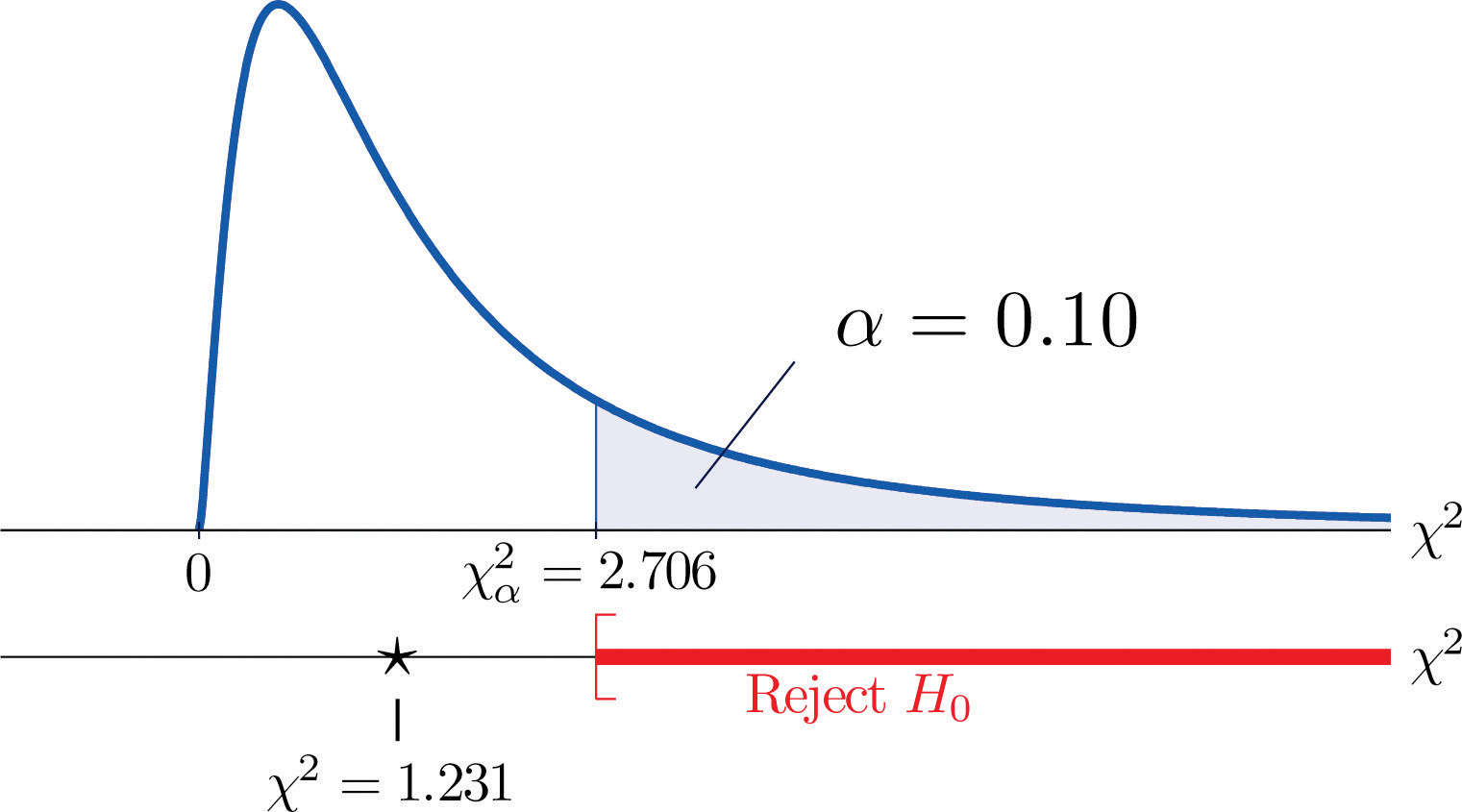
Med dette specifikke eksempel i baghovedet skal vi nu vende os til den generelle situation. I den generelle situation, hvor man tester uafhængigheden af to faktorer, kald dem faktor 1 og faktor 2, er de hypoteser, der skal testes, følgende
H0:De to faktorer er uafhængigevs. Ha:De to faktorer er ikke uafhængige
Som i eksemplet er hver faktor opdelt i et antal kategorier eller niveauer. Disse kan opstå naturligt, som i opdelingen dreng-pige af køn, eller noget arbitrært, som i opdelingen høj-lav af hjertefrekvens. Lad os antage, at faktor 1 har I-niveauer og faktor 2 har J-niveauer. Så giver oplysningerne fra en tilfældig stikprøve anledning til en generel I × J-kontingenstabel, som med rækketotaler, kolonnetotaler og en samlet totalsum ville se ud som vist i tabel 11.3 “Generel kontingenstabel”. Hver celle kan mærkes med et par indeks (i,j). Oij står for det observerede antal observationer i cellen i række i og kolonne j, Ri for den i-te samlede række og Cj for den j-te samlede kolonne. For at forenkle notationen vil vi droppe indeksene, så tabel 11.3 “Generel kontingenstabel” bliver til tabel 11.4 “Forenklet generel kontingenstabel”. Det er dog vigtigt at holde sig for øje, at Os, Rs og Cs, selv om de betegnes med de samme symboler, i virkeligheden er forskellige tal.
Tabel 11.3 Generel kontingenstabel
| Faktor 2 Niveauer | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Række i alt | ||||
| Faktor 1 Niveauer | 1 | O11 | – – – – | O1j | – – – – | O1J | R1 | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | Oi1 | – – – – | Oij | – – – – | OiJ | Ri | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OI1 | – – – – | OIj | – – – – | OIJ | RI | |||
| Spalte i alt | C1 | – – – – | Cj | – – – – | CJ | n | |||
Tabel 11.4 Forenklet generel kontingenstabel
| Faktor 2-niveauer | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Række i alt | |||
| Faktor 1 Niveauer | 1 | O | – – – – | O | – – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – – | O | – – – – | O | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | O | – – – – | O | – – – – | O | R | ||
| Spalte i alt | C | C | – – – – | C | – – – – | C | n | |
Som i eksemplet, for hver kernecelle i tabellen beregner vi, hvad der ville være det forventede antal E af observationer, hvis de to faktorer var uafhængige. E beregnes for hver kernecelle (hver celle med et O i) i tabel 11.4 “Simplified General Contingency Table” ved hjælp af den regel, der blev anvendt i eksemplet:
hvor R er rækketotalen og C er kolonnetotalen svarende til cellen, og n er stikprøvens størrelse.
Når det forventede antal er beregnet for hver celle, opdateres tabel 11.4 “Forenklet generel kontingenstabel” til tabel 11.5 “Opdateret generel kontingenstabel” ved at indsætte den beregnede værdi af E i hver enkelt kernecelle.
Tabel 11.5 Opdateret generel beredskabstabel
| Faktor 2-niveauer | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – – | J | Række i alt | ||||
| Faktor 1 Niveauer | 1 | OE | – – – – | OE | – – – – | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | OE | – – – – | OE | – – – – | OE | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OE | – – – – | OE | OE | – – – – | OE | R | ||
| Spalte i alt | C | – – – – | C | C | – – | C | n | ||
Her er teststatistikken for den generelle hypotese baseret på tabel 11.5 “Opdateret generel kontingenstabel”, sammen med betingelserne om, at den følger en chi-kvadratfordeling.
Teststatistik for test af uafhængigheden af to faktorer
χ2=Σ(O-E)2E
hvor summen er over alle kerneceller i tabellen.
Hvis
- de to undersøgelsesfaktorer er uafhængige, og
- det observerede antal O for hver celle i tabel 11.5 “Opdateret generel kontingenstabel” er mindst 5,
så følger χ2 omtrent en chi-square-fordeling med df=(I-1)×(J-1) frihedsgrader.
De samme procedurer i fem trin, enten den kritiske værditilgang eller p-værditilgangen, som blev introduceret i afsnit 8.1 “Elementerne i hypotesetestning” og afsnit 8.3 “Den observerede signifikans af en test” i kapitel 8 “Test af hypoteser”, anvendes til at udføre testen, som altid er højresvingende.
Eksempel 1
En forsker ønsker at undersøge, om elevernes resultater på en optagelsesprøve på college (CEE) har nogen indikativ kraft for fremtidige præstationer på college, målt ved GPA. Han ønsker med andre ord at undersøge, om faktorerne CEE og GPA er uafhængige eller ej. Han udvælger tilfældigt n = 100 studerende på et college og noterer hver enkelt studerendes score på optagelsesprøven og hans karaktergennemsnit ved udgangen af andet år på collegeuddannelsen. Han opdeler scoren ved optagelsesprøven i to niveauer og karaktergennemsnittet i tre niveauer. Ved at sortere dataene efter disse opdelinger danner han den tilfældighedstabel, der er vist som tabel 11.6 “CEE versus GPA Contingency Table”, hvor række- og kolonnetotalerne allerede er blevet beregnet.
Tabel 11.6 CEE versus GPA Contingency Table
| GPA | |||||
|---|---|---|---|---|---|
| <2,7 | 2,7 til 3,2 | >3.2 | Række I alt | ||
| CEE | 1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 18 | 48 |
| Spalte i alt | 41 | 36 | 23 | Total=100 | |
Test, på et signifikansniveau på 1 %, om disse data giver tilstrækkelige beviser til at konkludere, at CEE-scoringer indikerer fremtidige præstationsniveauer for indkommende førsteårsstuderende på college, målt ved GPA.
Løsning:
Vi udfører testen ved hjælp af den kritiske værditilgang og følger den sædvanlige femtrinsmetode, der er skitseret i slutningen af afsnit 8.1 “Elementerne i hypotesetestning” i kapitel 8 “Test af hypoteser”.
-
Trin 1. Hypoteserne er
H0:CEE og GPA er uafhængige faktorer vs. Ha:CEE og GPA er ikke uafhængige faktorer
- Stræk 2. Fordelingen er chi-square.
-
Stræk 3. For at beregne værdien af teststatistikken skal vi først beregne det forventede tal for hver af de seks kerneceller (dem, hvis poster er skrevet med fed skrift):
- 1. række og 1. kolonne: E=(R×C)∕n=41×52∕100=21,32
- 1. række og 2. kolonne:
- 1: E=(R×C)∕n=36×52∕100=18,72
- 1. række og 3. kolonne: E=(R×C)∕n=36×52∕100=18,72
- 1: E=(R×C)∕n=23×52∕100=11,96
- 2. række og 1. kolonne: E=(R×C)∕n=23×52∕100=11,96
- 2: E=(R×C)∕n=41×48∕100=19,68
- 2. række og 2. kolonne: E=(R×C)∕n=41×48∕100=19,68
- 2: E=(R×C)∕n=36×48∕100=17,28
- 2. række og 3. kolonne: E=(R×C)∕n=36×48∕100=17,28
- 2: E=(R×C)∕n=23×48∕100=11,04
Tabel 11.6 “CEE versus GPA-kontingenttabel” er opdateret til tabel 11.7 “Opdateret CEE versus GPA-kontingenttabel”.
Tabel 11.7 Opdateret CEE versus GPA-kontingenttabel
GPA <2.7 2.7 2.7 til 3,2 >3,2 Række I alt CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Spalte i alt C = 41 C = 36 C = 23 n = 100 Teststatistikken er
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Da CEE-faktoren har to niveauer og GPA-faktoren har tre, er I = 2 og J = 3. Teststatistikken følger således chi-square-fordelingen med df=(2-1)×(3-1)=2 frihedsgrader.
Da testen er højrehalet, er den kritiske værdi χ0,012. Når man læser fra figur 12.4 “Critical Values of Chi-Square Distributions”, er χ0,012=9,210, så afvisningsområdet er [9,210,∞).
- Stræk 5. Da 31,75 > 9,21 er beslutningen at forkaste nulhypotesen. Se figur 11.4. Dataene giver tilstrækkelig dokumentation på et signifikansniveau på 1 % til at konkludere, at CEE-scoren og GPA ikke er uafhængige: Optagelsesprøvens score har en forudsigelseskraft.
Figur 11.4 Note 11.9 “Eksempel 1”
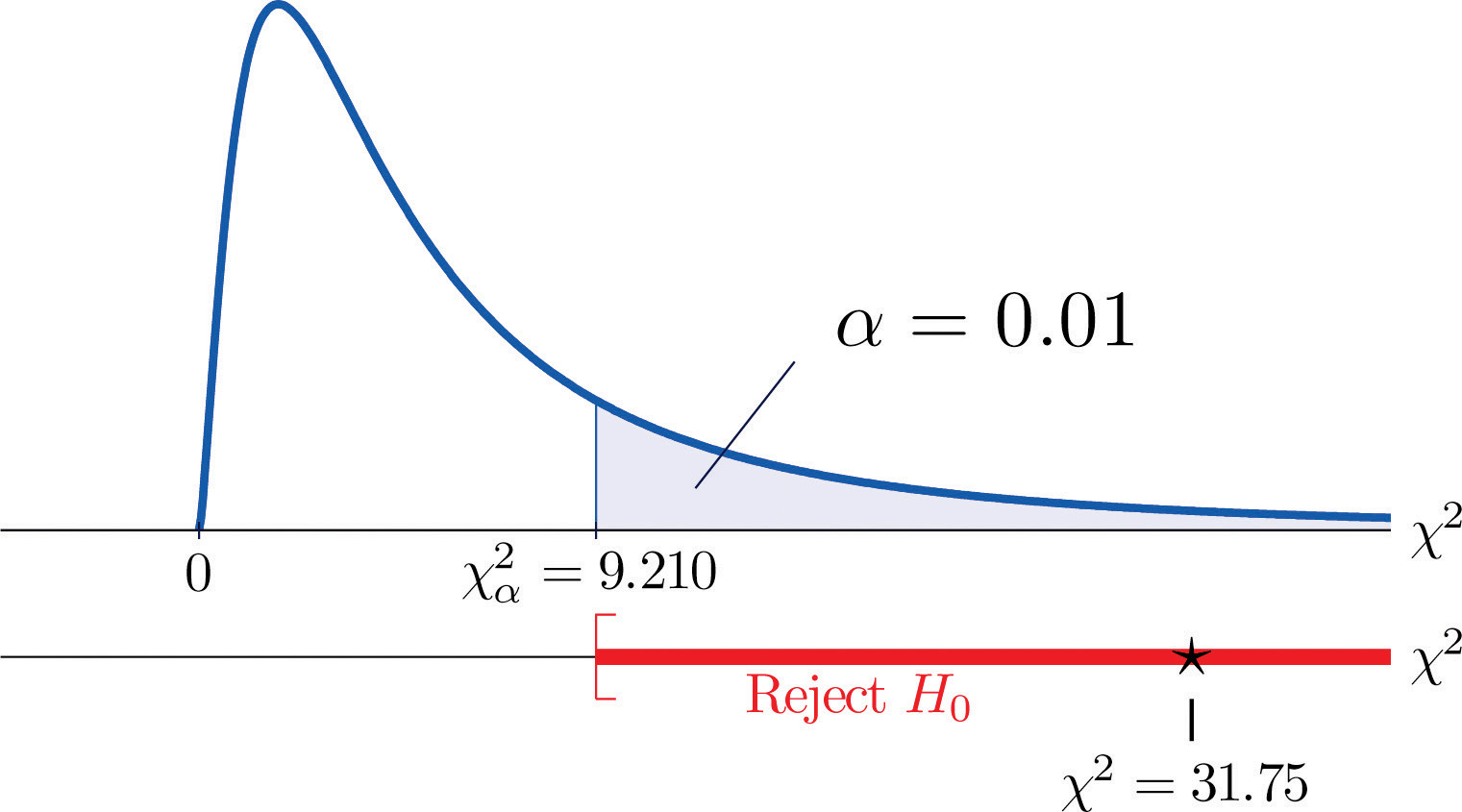
Nøgleudbytte
- Kritiske værdier for en chi-square-fordeling med frihedsgrader df findes i figur 12.4 “Kritiske værdier af chi-kvadratfordelinger”.
- En chi-kvadrattestEn test baseret på en chi-kvadratstatistik til at kontrollere, om to faktorer er uafhængige. kan bruges til at vurdere hypotesen om, at to tilfældige variabler eller faktorer er uafhængige.
Opgaver
Grundlæggende
-
Find χ0,012 for hvert af følgende antal frihedsgrader.
- df=5
- df=11
- df=25
-
Søg χ0,052 for hvert af følgende antal frihedsgrader.
- df=6
- df=12
- df=30
-
Find χ0.102 for hvert af følgende antal frihedsgrader.
- df=6
- df=12
- df=30
-
Find χ0.012 for hvert af følgende antal frihedsgrader.
- df=7
- df=10
- df=20
-
For df=7 og α=0.05, find
- χα2
- χα22
-
For df=17 og α=0.01, find
- χα2
- χα22
-
En dataprøve er sorteret i en 2 × 2 kontingenstabel baseret på to faktorer, som hver har to niveauer.
Faktor 1
Niveau 1
Niveau 2
Række i alt
Faktor 2
Niveau 1
20
10
10
R
Niveau 2
15
5
R
Spaltsum
C
C
C
n
- Find kolonnesummen, rækketotalerne og den samlede totalsum, n, for tabellen.
- Find det forventede antal E af observationer for hver celle ud fra den antagelse, at de to faktorer er uafhængige (dvs. brug blot formlen E=(R×C)∕n).
- Find værdien af chi-square-teststatistikken χ2.
- Find antallet af frihedsgrader for chi-kvadrat-teststatistikken.
Grundlæggende
Find χ0,012 for hvert af følgende antal frihedsgrader.
- df=5
- df=11
- df=25
Søg χ0,052 for hvert af følgende antal frihedsgrader.
- df=6
- df=12
- df=30
Find χ0.102 for hvert af følgende antal frihedsgrader.
- df=6
- df=12
- df=30
Find χ0.012 for hvert af følgende antal frihedsgrader.
- df=7
- df=10
- df=20
For df=7 og α=0.05, find
- χα2
- χα22
For df=17 og α=0.01, find
- χα2
- χα22
En dataprøve er sorteret i en 2 × 2 kontingenstabel baseret på to faktorer, som hver har to niveauer.
| Faktor 1 | |||||
|---|---|---|---|---|---|
| Niveau 1 | Niveau 2 | Række i alt | |||
| Faktor 2 | Niveau 1 | 20 | 10 | 10 | R |
| Niveau 2 | 15 | 5 | R | ||
| Spaltsum | C | C | C | n | |
- Find kolonnesummen, rækketotalerne og den samlede totalsum, n, for tabellen.
- Find det forventede antal E af observationer for hver celle ud fra den antagelse, at de to faktorer er uafhængige (dvs. brug blot formlen E=(R×C)∕n).
- Find værdien af chi-square-teststatistikken χ2.
- Find antallet af frihedsgrader for chi-kvadrat-teststatistikken.
En dataprøve er sorteret i en 3 × 2 kontingenstabel baseret på to faktorer, hvoraf den ene har tre niveauer og den anden har to niveauer.
| Faktor 1 | |||||
|---|---|---|---|---|---|
| Niveau 1 | Niveau 2 | Række i alt | |||
| Faktor 2 | Niveau 1 | 20 | 10 | R | R |
| Niveau 2 | 15 | 5 | R | ||
| Niveau 3 | 10 | 20 | R | R | |
| Spaltsum | C | C | C | n | |
- Find kolonnesummen, rækketotalerne og den samlede totalsum, n, for tabellen.
- Find det forventede antal E af observationer for hver celle ud fra den antagelse, at de to faktorer er uafhængige (dvs. brug blot formlen E=(R×C)∕n).
- Find værdien af chi-square-teststatistikken χ2.
- Find antallet af frihedsgrader for chi-kvadrat-teststatistikken.
-
En børnepsykolog mener, at børn klarer sig bedre til prøver, når de får en opfattet valgfrihed. For at teste denne overbevisning udførte psykologen et eksperiment, hvor 200 børn i tredje klasse blev tilfældigt fordelt på to grupper, A og B. Hvert barn fik den samme enkle logiske test. I gruppe B fik hvert barn imidlertid frihed til at vælge et teksthæfte blandt mange med forskellige tegninger på forsiderne. Hvert barns præstation blev vurderet som meget god, god og rimelig. Resultaterne er opsummeret i tabellen. Test med et signifikansniveau på 5 %, om der er tilstrækkelig dokumentation i dataene til at understøtte psykologens overbevisning.
Gruppe A B Performance Very Good 32 29 God 55 61 Middelmådig 10 13 -
Med hensyn til konkurrencer i forbindelse med vinsmagning, mange eksperter hævder, at det første glas vin, der serveres, sætter en referencesmag, og at en anden referencevin kan ændre den relative placering af de andre vine i konkurrencen. For at teste denne påstand blev der serveret tre vine, A, B og C, ved en vinsmagning. Hver person fik serveret et enkelt glas af hver vin, men i forskellige rækkefølger for de forskellige gæster. Ved afslutningen blev hver person bedt om at nævne den bedste af de tre vine. Der var 172 personer til stede ved arrangementet, og deres bedste valg er angivet i tabellen. Test med et signifikansniveau på 1 %, om der er tilstrækkelig dokumentation i dataene til at understøtte påstanden om, at vineksperternes præference er afhængig af den først serverede vin.
Topvalg A B B C Første glas A 12 31 31 27 B 15 40 21 C C 10 9 7 -
Er ved at blive efterladt-håndleddet arveligt? For at besvare dette spørgsmål udvælges 250 voksne tilfældigt, og deres og deres forældres håndledighed noteres. Resultaterne er opsummeret i den medfølgende tabel. Test med et signifikansniveau på 1 %, om der er tilstrækkeligt belæg i dataene til at konkludere, at der er et arveligt element i håndledighed.
Antal af forældre venstrehåndedeHanded 0 1 2 Handedness Links 8 10 12 Højre 178 21 21 -
Nogle genetikere hævder, at generne, der bestemmer venstre-venstrehåndethed også styrer udviklingen af sprogcentrene i hjernen. Hvis denne påstand er sand, ville det være rimeligt at forvente, at venstrehåndede mennesker har en tendens til at have stærkere sproglige evner. I en undersøgelse, der skulle belyse denne påstand, blev der tilfældigt udvalgt 807 studerende, som tog Graduate Record Examination (GRE). Deres resultater på den sproglige del af eksamen blev inddelt i tre kategorier: lav, gennemsnitlig og høj, og deres håndledighed blev også noteret. Resultaterne er angivet i den medfølgende tabel. Test, på et signifikansniveau på 5 %, om der er tilstrækkelig dokumentation i dataene til at konkludere, at venstrehåndede personer har tendens til at have stærkere sproglige evner.
GRE English Scores Low Average Høj Håndfærdighed Venstre 18 18 40 22 Højre 201 360 166 -
Det er en generel opfattelse, at børn, der vokser op i stabile familier, har en tendens til at klare sig godt i skolen. For at verificere en sådan opfattelse undersøgte en samfundsvidenskabelig forsker 290 tilfældigt udvalgte elevers journaler i en offentlig gymnasieskole og noterede hver enkelt elevs familiestruktur og akademiske status fire år efter, at de var begyndt på gymnasiet. Dataene blev derefter sorteret i en 2 × 3 kontingenstabel med to faktorer. Faktor 1 har to niveauer: “dimitteret” og “ikke dimitteret”. Faktor 2 har tre niveauer: ingen forældre, en forælder og to forældre. Resultaterne fremgår af den vedlagte tabel. Test på et signifikansniveau på 1 %, om der er tilstrækkeligt bevis i dataene til at konkludere, at familiestrukturen har betydning for elevernes skolepræstationer.
Akademisk status Afgangseksamen Afgangseksamen ikke Familie Ingen forældre 18 18 31 En forælder 101 44 To forældre 70 26 -
En stor mellemskoleadministrator ønsker at bruge kendissernes indflydelse til at tilskynde eleverne til at træffe sundere valg i skolens cafeteria. Cafeteriet ligger i midten af et åbent område. Hver dag ved frokosttid får eleverne deres frokost og en drink i tre separate rækker, der fører til tre separate serveringsstationer. Som et eksperiment har skolelederen hængt en plakat op med en populær teenagepopstjerne, der drikker mælk ved hvert af de tre områder, hvor der serveres drikkevarer, bortset fra at mælken på plakaten er forskellig på hvert sted: et sted er der hvid mælk, et sted er der pink mælk med jordbærsmag, og et sted er der chokolademælk. Efter den første dag af forsøget noterede administratoren elevernes mælkevalg separat for de tre linjer. Dataene er anført i den medfølgende tabel. Test med et signifikansniveau på 1 %, om der er tilstrækkelig dokumentation i dataene til at konkludere, at plakaterne havde en vis indflydelse på elevernes valg af drikkevarer.
Studenternes valg Regulært Strawberry Strawberry Chocolate Plakatvalg Regulært 38 28 40 Strawberry 18 18 51 24 Chokolade 32 32 32 53
Anvendelser
-
Large Datasæt 8 indeholder resultatet af en undersøgelse af 300 tilfældigt udvalgte voksne, der regelmæssigt går i biografen. For hver person blev køn og den foretrukne type film registreret. Test med et signifikansniveau på 5 %, om der er tilstrækkelig dokumentation i dataene til at konkludere, at faktorerne “køn” og “foretrukken type film” er afhængige.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Large Datasæt Øvelse
Svar
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5.99, forkaster ikke H0
-
χ2=72.35, χ0.012=9.21, forkaster H0
-
χ2=21.2784, χ0.012=9.21, forkastes H0
-
χ2=28.4539. df=3. Afvisningsområde: [7.815,∞). Afgørelse: Afvisning af H0 for uafhængighed.