Tests d’indépendance
Les tests d’hypothèses rencontrés plus tôt dans le livre avaient trait à la façon dont les valeurs numériques de deux paramètres de la population se comparaient. Dans cette sous-section, nous étudierons des hypothèses qui ont à voir avec le fait que deux variables aléatoires prennent leurs valeurs indépendamment ou non, ou que la valeur de l’une a une relation avec la valeur de l’autre. Les hypothèses seront donc exprimées en mots, et non en symboles mathématiques. Nous construisons la discussion autour de l’exemple suivant.
Il existe une théorie selon laquelle le sexe d’un bébé dans l’utérus est lié au rythme cardiaque du bébé : les bébés filles ont tendance à avoir un rythme cardiaque plus élevé. Supposons que nous souhaitions tester cette théorie. Nous examinons les enregistrements du rythme cardiaque de 40 bébés pris lors des derniers contrôles prénataux de leurs mères avant l’accouchement, et à chacun de ces 40 enregistrements choisis au hasard, nous calculons les valeurs de deux mesures aléatoires : 1) le sexe et 2) le rythme cardiaque. Dans ce contexte, ces deux mesures aléatoires sont souvent appelées facteursUne variable avec plusieurs niveaux qualitatifs . Puisque la charge de la preuve est que la fréquence cardiaque et le sexe sont liés, et non qu’ils ne sont pas liés, le problème du test de la théorie sur le sexe et la fréquence cardiaque du bébé peut être formulé comme un test des hypothèses suivantes :
H0:Le sexe du bébé et la fréquence cardiaque du bébé sont indépendantsvs. Ha:Le sexe du bébé et la fréquence cardiaque du bébé ne sont pas indépendants
Le facteur sexe a deux catégories ou niveaux naturels : garçon et fille. Nous divisons le second facteur, la fréquence cardiaque, en deux niveaux, faible et élevé, en choisissant une certaine fréquence cardiaque, disons 145 battements par minute, comme seuil entre les deux. Une fréquence cardiaque inférieure à 145 battements par minute sera considérée comme faible et 145 et plus comme élevée. Les 40 enregistrements donnent lieu à un tableau de contingence 2 × 2. En joignant les totaux des lignes, les totaux des colonnes et un total général, on obtient le tableau 11.1 « Sexe du bébé et fréquence cardiaque ». Les quatre entrées en caractères gras correspondent au nombre d’observations de l’échantillon de n = 40. Il y avait 11 filles avec une fréquence cardiaque basse, 17 garçons avec une fréquence cardiaque basse, et ainsi de suite. Elles forment le noyau du tableau développé.
Tableau 11.1 Sexe du bébé et fréquence cardiaque
| Fréquence cardiaque | ||||
|---|---|---|---|---|
| Low | High | Total des rangs | ||
| Gender | Girl | 11 | 7 | 18 |
| Boy | 17 | 5 | 22 | |
| Total des colonnes | 28 | 12 | Total = 40 | |
Par analogie avec le fait que la probabilité d’événements indépendants est le produit des probabilités de chaque événement, si la fréquence cardiaque et le sexe étaient indépendants, nous nous attendrions à ce que le nombre dans chaque cellule centrale soit proche du produit du total de la ligne R et du total de la colonne C de la ligne et de la colonne qui la contiennent, divisé par la taille n de l’échantillon. En dénotant un tel nombre attendu d’observations E, ces quatre valeurs attendues sont :
- 1ère ligne et 1ère colonne : E=(R×C)∕n=18×28∕40=12,6
- 1ère ligne et 2ème colonne : E=(R×C)∕n=18×12∕40=5,4
- 2ème ligne et 1ère colonne : E=(R×C)∕n=22×28∕40=15,4
- 2ème ligne et 2ème colonne : E=(R×C)∕n=22×12∕40=6,6
Nous mettons à jour le tableau 11.1 » Sexe et fréquence cardiaque du bébé » en plaçant chaque valeur attendue dans sa cellule centrale correspondante, juste en dessous de la valeur observée dans la cellule. Cela donne le tableau mis à jour Tableau 11.2 « Sexe et rythme cardiaque du bébé mis à jour ».
Tableau 11.2 Sexe du bébé et fréquence cardiaque actualisés
| Fréquence cardiaque | ||||
|---|---|---|---|---|
| Low | Haut | Total des rangs | ||
| Gender | Girl | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Boy | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Total des colonnes | C = 28 | C = 12 | n = 40 | |
Une mesure de l’écart entre les données et ce que nous nous attendrions à voir si les facteurs étaient vraiment indépendants est la somme des carrés de la différence des nombres dans chaque cellule centrale, ou, en normalisant en divisant chaque carré par le nombre attendu dans la cellule, la somme Σ(O-E)2∕E. Nous ne rejetterions l’hypothèse nulle selon laquelle les facteurs sont indépendants que si ce nombre est grand, le test est donc unilatéral. Dans cet exemple, la variable aléatoire Σ(O-E)2∕E a la distribution du chi carré avec un degré de liberté. Si nous avions décidé au départ de tester au niveau de signification de 10 %, la valeur critique définissant la région de rejet serait, si l’on lit la figure 12.4 « Valeurs critiques des distributions du chi-deux », χα2=χ0,102=2,706, de sorte que la région de rejet serait l’intervalle [2,706,∞). Lorsque nous calculons la valeur de la statistique de test standardisée, nous obtenons
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Puisque 1,231 < 2,706, la décision est de ne pas rejeter H0. Voir la figure 11.3 « Prédiction du sexe du bébé ». Les données ne fournissent pas de preuves suffisantes, au niveau de signification de 10%, pour conclure que la fréquence cardiaque et le sexe sont liés.
Figure 11.3 Prédiction du sexe du bébé
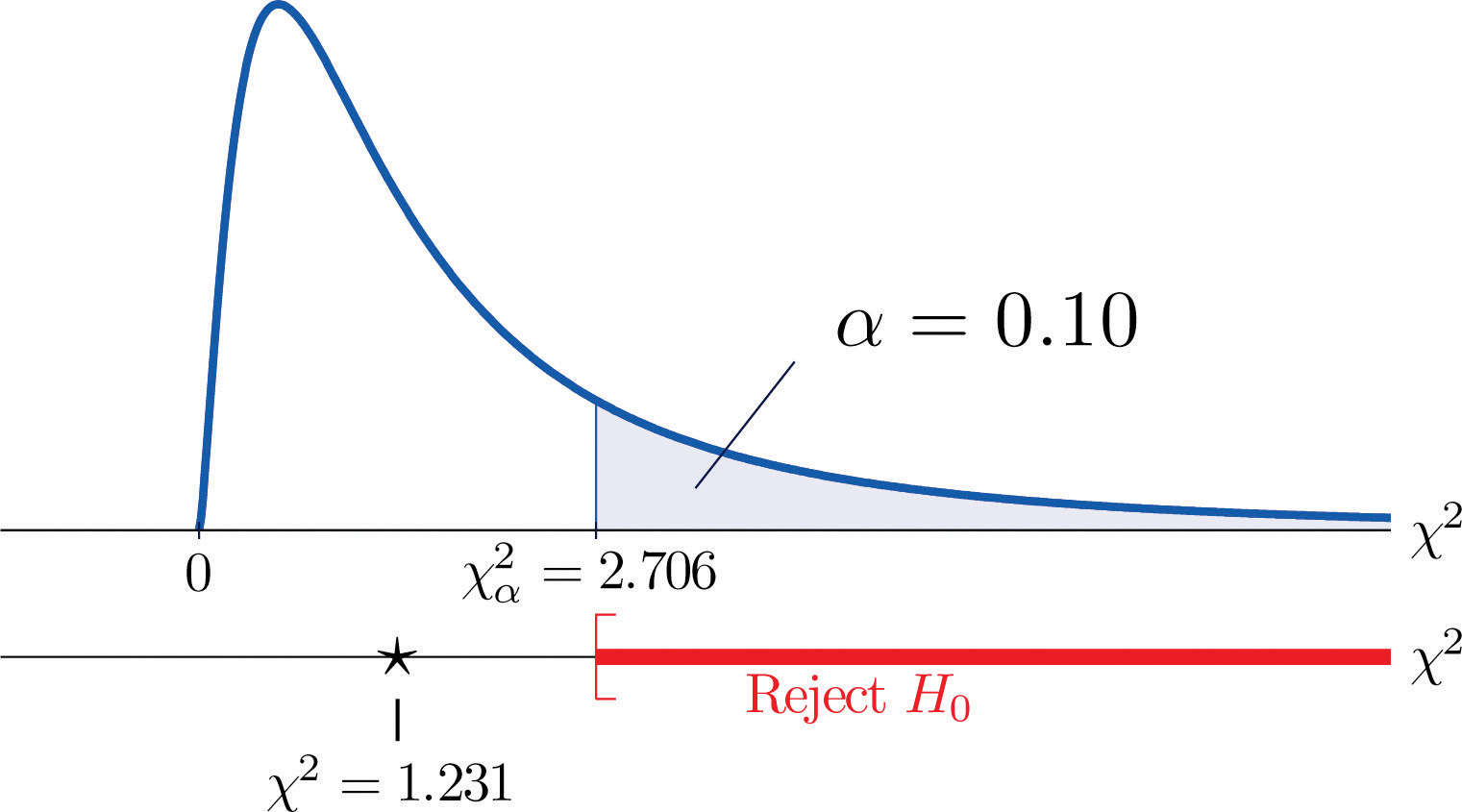
Avec cet exemple spécifique en tête, passons maintenant à la situation générale. Dans le cadre général du test de l’indépendance de deux facteurs, appelons-les Facteur 1 et Facteur 2, les hypothèses à tester sont
H0:Les deux facteurs sont indépendantsvs. Ha:Les deux facteurs ne sont pas indépendants
Comme dans l’exemple, chaque facteur est divisé en un certain nombre de catégories ou de niveaux. Ceux-ci pourraient apparaître naturellement, comme dans la division garçon-fille du sexe, ou quelque peu arbitrairement, comme dans la division haut-bas de la fréquence cardiaque. Supposons que le facteur 1 ait des niveaux I et que le facteur 2 ait des niveaux J. Les informations provenant d’un échantillon aléatoire donnent alors lieu à un tableau de contingence général I × J, qui, avec les totaux des lignes, les totaux des colonnes et un total général, apparaîtrait comme indiqué dans le tableau 11.3 « Tableau de contingence général ». Chaque cellule peut être étiquetée par une paire d’indices (i,j). Oij représente le nombre observé d’observations dans la cellule à la ligne i et à la colonne j, Ri le total de la ième ligne et Cj le total de la jième colonne. Pour simplifier la notation, nous allons supprimer les indices, de sorte que le tableau 11.3 « Tableau de contingence général » devient le tableau 11.4 « Tableau de contingence général simplifié ». Néanmoins il est important de garder à l’esprit que les Os, les R et les C, bien que dénotés par les mêmes symboles, sont en fait des nombres différents.
Tableau 11.3 Tableau général des contingences
| Niveaux du facteur 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Total des rangs | ||
| Niveaux du facteur 1 | 1 | O11 | – – – | O1j | – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – | Oij | – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OI1 | – – – | OIj | – – – | OIJ | RI | |
| Total des colonnes | C1 | – – – | Cj | – – | CJ | n | |
Tableau 11.4 Tableau général simplifié des contingences
| Niveaux du facteur 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Total des rangs | ||
| Niveaux du facteur 1 | 1 | O | – – – | O | – – – | O | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – | O | – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| I | O | – – – | O | – – – | O | R | |
| Total de la colonne | C | – – – | C | – – – | C | n | |
Comme dans l’exemple, pour chaque cellule centrale du tableau, nous calculons quel serait le nombre attendu E d’observations si les deux facteurs étaient indépendants. E est calculé pour chaque cellule centrale (chaque cellule contenant un O) du tableau 11.4 « Tableau de contingence général simplifié » par la règle appliquée dans l’exemple :
où R est le total de la ligne et C est le total de la colonne correspondant à la cellule, et n est la taille de l’échantillon.
Après avoir calculé le nombre attendu pour chaque cellule, le tableau 11.4 « Tableau général simplifié des contingences » est mis à jour pour former le tableau 11.5 « Tableau général actualisé des contingences » en insérant la valeur calculée de E dans chaque cellule centrale.
Tableau 11.5 Tableau général actualisé des imprévus
| Niveaux du facteur 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – | J | Total des rangs | ||
| Niveaux du facteur 1 | 1 | OE | – – – | OE | – – – | OE | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | OE | – – – | OE | – – | OE | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – – | OE | – – – | OE | R | |
| Total de la colonne | C | – – | C | – – | C | n | |
Voici la statistique de test pour l’hypothèse générale basée sur le tableau 11.5 « Tableau de contingence général mis à jour », ainsi que les conditions pour qu’elle suive une distribution chi-carré.
Statistique de test pour tester l’indépendance de deux facteurs
χ2=Σ(O-E)2E
où la somme est sur toutes les cellules centrales du tableau.
Si
- les deux facteurs d’étude sont indépendants, et
- le nombre observé O de chaque cellule du tableau 11.5 « Tableau de contingence général mis à jour » est d’au moins 5,
alors χ2 suit approximativement une distribution chi-carré avec df=(I-1)×(J-1) degrés de liberté.
Les mêmes procédures en cinq étapes, soit l’approche de la valeur critique, soit l’approche de la valeur p, qui ont été introduites dans la section 8.1 « Les éléments du test d’hypothèse » et la section 8.3 « La signification observée d’un test » du chapitre 8 « Test d’hypothèses » sont utilisées pour effectuer le test, qui est toujours à queue droite.
Exemple 1
Un chercheur souhaite étudier si les résultats des étudiants à un examen d’entrée au collège (CEE) ont un quelconque pouvoir indicatif de la performance future au collège, mesurée par la moyenne générale. En d’autres termes, il souhaite déterminer si les facteurs CEE et GPA sont indépendants ou non. Il choisit au hasard n = 100 étudiants dans un collège et note le score de chaque étudiant à l’examen d’entrée et sa moyenne générale à la fin de la deuxième année. Il divise les résultats de l’examen d’entrée en deux niveaux et les moyennes en trois niveaux. En triant les données selon ces divisions, il forme le tableau de contingence présenté dans le tableau 11.6 « Tableau de contingence CEE versus GPA », dans lequel les totaux des lignes et des colonnes ont déjà été calculés.
Tableau 11.6 Tableau de contingence CEE versus GPA
| GPA | |||||
|---|---|---|---|---|---|
| <2,7 | 2,7 à 3,2 | >3.2 | Rangée Total | ||
| CEE | <1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Total des colonnes | 41 | 36 | 23 | Total=100 | |
Test, au niveau de signification de 1%, si ces données fournissent des preuves suffisantes pour conclure que les scores CEE indiquent les niveaux de performance futurs des étudiants entrants en première année de collège, tels que mesurés par la GPA.
Solution:
Nous effectuons le test en utilisant l’approche de la valeur critique, en suivant la méthode habituelle en cinq étapes décrite à la fin de la section 8.1 « Les éléments du test d’hypothèse » du chapitre 8 « Tester des hypothèses ».
-
Étape 1. Les hypothèses sont
H0:CEE et GPA sont des facteurs indépendantsvs. Ha:CEE et GPA ne sont pas des facteurs indépendants
- Étape 2. La distribution est le chi carré.
-
Étape 3. Pour calculer la valeur de la statistique de test, nous devons d’abord calculer le nombre attendu pour chacune des six cellules centrales (celles dont les entrées sont en gras) :
- 1ère ligne et 1ère colonne : E=(R×C)∕n=41×52∕100=21,32
- 1ère ligne et 2ème colonne : E=(R×C)∕n=36×52∕100=18.72
- 1ère ligne et 3ème colonne : E=(R×C)∕n=23×52∕100=11.96
- 2ème ligne et 1ère colonne : E=(R×C)∕n=41×48∕100=19.68
- 2ème ligne et 2ème colonne : E=(R×C)∕n=36×48∕100=17.28
- 2ème ligne et 3ème colonne : E=(R×C)∕n=23×48∕100=11.04
Tableau 11.6 « Tableau de contingence CEE versus GPA » est mis à jour en Tableau 11.7 « Tableau de contingence CEE versus GPA mis à jour ».
Tableau 11.7 Mise à jour du tableau de contingence du CEE par rapport à la moyenne générale
GPA 2.7 2.7 à 3.2 >3.2 Rangée Total CEE 1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Total des colonnes C = 41 C = 36 C = 23 n = 100 La statistique du test est
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Comme le facteur CEE a deux niveaux et le facteur GPA en a trois, I = 2 et J = 3. Ainsi, la statistique du test suit la distribution du chi-deux avec df=(2-1)×(3-1)=2 degrés de liberté.
Comme le test est à queue droite, la valeur critique est χ0,012. En lisant la figure 12.4 « Valeurs critiques des distributions de khi-deux », χ0,012=9,210, donc la région de rejet est [9,210,∞).
- Étape 5. Puisque 31,75 > 9,21, la décision est de rejeter l’hypothèse nulle. Voir la figure 11.4. Les données fournissent suffisamment de preuves, au niveau de signification de 1 %, pour conclure que le score à l’EEC et la GPA ne sont pas indépendants : le score à l’examen d’entrée a un pouvoir prédictif.
Figure 11.4 Note 11.9 « Exemple 1 »
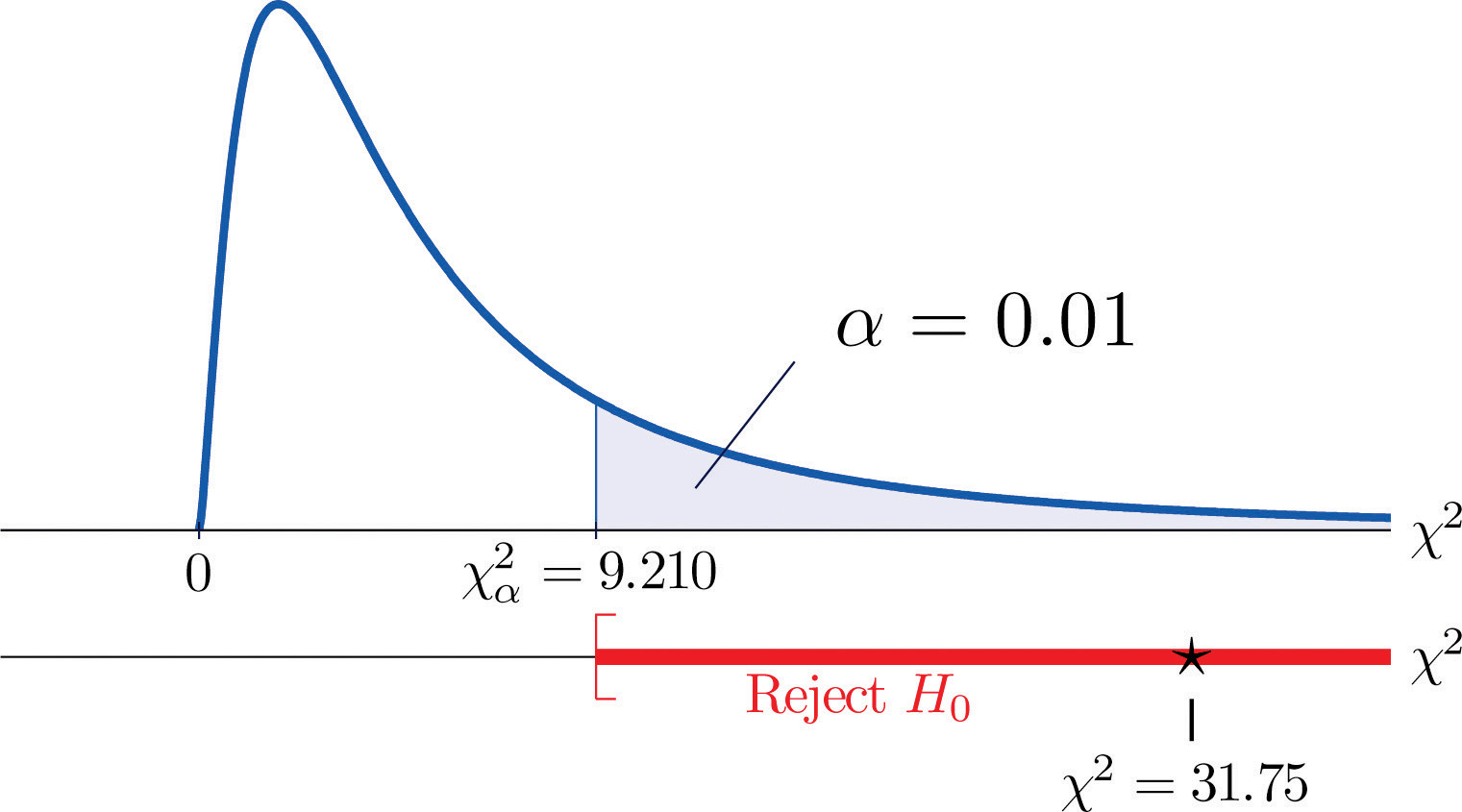
Principaux enseignements
- Les valeurs critiques d’une distribution du chi-deux avec des degrés de liberté df se trouvent dans la figure 12.4 « Valeurs critiques des distributions du chi carré ».
- Test du chi carréUn test basé sur une statistique du chi carré pour vérifier si deux facteurs sont indépendants. peut être utilisé pour évaluer l’hypothèse que deux variables aléatoires ou facteurs sont indépendants.
Exercices
-
Trouver χ0,012 pour chacun des nombres de degrés de liberté suivants.
- df=5
- df=11
- df=25
-
Trouver χ0,052 pour chacun des nombres de degrés de liberté suivants.
- df=6
- df=12
- df=30
-
Trouve χ0.102 pour chacun des nombres de degrés de liberté suivants.
- df=6
- df=12
- df=30
-
Find χ0.012 pour chacun des nombres de degrés de liberté suivants.
- df=7
- df=10
- df=20
-
Pour df=7 et α=0.05, trouver
- χα2
- χα22
-
Pour df=17 et α=0.01, trouver
- χα2
- χα22
-
Un échantillon de données est trié dans un tableau de contingence 2 × 2 basé sur deux facteurs, chacun ayant deux niveaux.
Facteur 1 Niveau 1 .
Niveau 2 Total ligne Facteur 2 Niveau 1 20 10 R Niveau 2 15 5 R Total des colonnes C C n - Trouver les totaux des colonnes, les totaux des lignes et le total général, n, du tableau.
- Trouvez le nombre attendu E d’observations pour chaque cellule en partant de l’hypothèse que les deux facteurs sont indépendants (c’est-à-dire qu’il suffit d’utiliser la formule E=(R×C)∕n).
- Trouvez la valeur de la statistique du test du chi-deux χ2.
- Trouvez le nombre de degrés de liberté de la statistique du test du chi carré.
-
Un échantillon de données est trié dans un tableau de contingence 3 × 2 basé sur deux facteurs, dont l’un a trois niveaux et l’autre deux niveaux.
Facteur 1 Niveau 1 Niveau 2 .
Total ligne Facteur 2 Niveau 1 20 10 R Niveau 2 15 5 R Niveau 3 10 20 R Total des colonnes C C n - Trouver les totaux des colonnes, les totaux des lignes et le total général, n, du tableau.
- Trouvez le nombre attendu E d’observations pour chaque cellule en partant de l’hypothèse que les deux facteurs sont indépendants (c’est-à-dire qu’il suffit d’utiliser la formule E=(R×C)∕n).
- Trouvez la valeur de la statistique du test du chi-deux χ2.
- Trouvez le nombre de degrés de liberté de la statistique du test du chi carré.
Basique
-
Un psychologue pour enfants croit que les enfants réussissent mieux les tests lorsqu’on leur donne une liberté de choix perçue. Pour tester cette croyance, le psychologue a mené une expérience dans laquelle 200 élèves de troisième année ont été répartis au hasard en deux groupes, A et B. Chaque enfant a été soumis au même test de logique simple. Cependant, dans le groupe B, chaque enfant avait la liberté de choisir un livret de texte parmi de nombreux autres dont la couverture était ornée de divers dessins. La performance de chaque enfant a été évaluée comme suit : très bonne, bonne et moyenne. Les résultats sont résumés dans le tableau fourni. Testez, au niveau de signification de 5%, s’il y a suffisamment de preuves dans les données pour soutenir la croyance du psychologue.
Groupe A B Performance Très bonne 32 29 .
Bonne 55 61 Parfaite 10 13 -
En ce qui concerne les concours de dégustation de vin, de nombreux experts affirment que le premier verre de vin servi fixe un goût de référence et qu’un vin de référence différent peut modifier le classement relatif des autres vins en compétition. Pour tester cette affirmation, trois vins, A, B et C, ont été servis lors d’une dégustation de vins. Chaque personne s’est vue servir un seul verre de chaque vin, mais dans des ordres différents selon les invités. À la fin de la dégustation, on a demandé à chaque personne de nommer le meilleur des trois vins. Cent soixante-douze personnes ont participé à l’événement et leurs choix sont indiqués dans le tableau ci-dessous. Testez, au niveau de signification de 1%, s’il y a suffisamment de preuves dans les données pour soutenir l’affirmation selon laquelle la préférence des experts en vin dépend du premier vin servi.
Top Pick A B .
C Premier verre A 12 31 27 B 15 40 21 C 10 9 7 -
Est-ce que le fait d’être gauchergaucher est-il héréditaire ? Pour répondre à cette question, 250 adultes sont choisis au hasard et leur gaucherie ainsi que celle de leurs parents sont notées. Les résultats sont résumés dans le tableau fourni. Testez, au niveau de signification de 1%, s’il y a suffisamment de preuves dans les données pour conclure qu’il y a un élément héréditaire dans la gaucherie.
Nombre de parents gauchers .Gauche
0 1 2 Manipotence Gauche 8 10 12 Droit 178 21 21 -
Certains généticiens affirment que les gènes qui déterminent la gaucherie régissent également le développement du langage.gauchers régissent également le développement des centres du langage dans le cerveau. Si cette affirmation est vraie, il serait alors raisonnable de s’attendre à ce que les gauchers aient tendance à avoir des capacités linguistiques plus fortes. Dans le cadre d’une étude visant à vérifier cette affirmation, 807 étudiants ont été sélectionnés au hasard pour passer le Graduate Record Examination (GRE). Leurs résultats à la partie linguistique de l’examen ont été classés en trois catégories : faible, moyen et élevé, et leur gaucherie a également été notée. Les résultats sont présentés dans le tableau fourni. Testez, au niveau de signification de 5 %, s’il y a suffisamment de preuves dans les données pour conclure que les gauchers ont tendance à avoir des capacités linguistiques plus fortes.
Score d’anglais du GRE Bas Moyen .
Élevée Manipulation Gauche 18 40 .
22 Droit 201 360 166 -
On croit généralement que les enfants élevés dans des familles stables ont tendance à bien réussir à l’école. Pour vérifier une telle croyance, un spécialiste des sciences sociales a examiné les dossiers de 290 élèves choisis au hasard dans un lycée public et a noté la structure familiale et le statut scolaire de chaque élève quatre ans après son entrée au lycée. Les données ont ensuite été classées dans un tableau de contingence 2 × 3 comportant deux facteurs. Le facteur 1 comporte deux niveaux : diplômé et non diplômé. Le facteur 2 comporte trois niveaux : aucun parent, un parent et deux parents. Les résultats sont donnés dans le tableau fourni. Testez, au niveau de signification de 1%, s’il y a suffisamment de preuves dans les données pour conclure que la structure familiale a de l’importance dans les performances scolaires des élèves.
Situation scolaire Diplômé Non diplômé .
Famille Pas de parent 18 31 Un parent 101 44 Deux parents 70 26 -
L’administrateur d’un grand collège souhaite utiliser l’influence de la célébrité pour encourager les élèves à faire des choix plus sains à la cafétéria de l’école. La cafétéria est située au centre d’un espace ouvert. Tous les jours, à l’heure du déjeuner, les élèves prennent leur repas et une boisson dans trois lignes distinctes menant à trois stations de service séparées. À titre d’expérience, l’administrateur de l’école a affiché un poster d’une pop star adolescente populaire buvant du lait à chacun des trois endroits où des boissons sont servies, sauf que le lait sur le poster est différent à chaque endroit : l’un montre du lait blanc, l’autre du lait rose aromatisé à la fraise et le dernier du lait au chocolat. Après le premier jour de l’expérience, l’administrateur a noté les choix de lait des élèves séparément pour les trois lignes. Les données sont indiquées dans le tableau fourni. Testez, au niveau de signification de 1%, s’il y a suffisamment de preuves dans les données pour conclure que les affiches ont eu un certain impact sur les choix de boissons des élèves.
Choix de l’étudiant Régulier Fraise Chocolat .
Choix de l’affiche Régulier 38 28 40 Fraise 18 .
51 24 Chocolat 32 32 53
Applications
-
Large L’ensemble de données 8 enregistre le résultat d’une enquête auprès de 300 adultes sélectionnés au hasard qui vont régulièrement au cinéma. Pour chaque personne, le sexe et le type de film préféré ont été enregistrés. Testez, au niveau de signification de 5%, s’il y a suffisamment de preuves dans les données pour conclure que les facteurs « sexe » et « type de film préféré » sont dépendants.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Grande taille Exercice sur les ensembles de données
Réponses
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5,99, ne pas rejeter H0
-
χ2=72,35, χ0,012=9,21, rejeter H0
-
χ2=21.2784, χ0.012=9.21, rejeter H0
-
χ2=28.4539. df=3. Région de rejet : [7.815,∞). Décision : Rejeter H0 de l’indépendance.
.