Test för oberoende
Hypotest som vi har träffat på tidigare i boken handlade om hur de numeriska värdena för två populationsparametrar jämfördes. I det här underavsnittet kommer vi att undersöka hypoteser som har att göra med om två slumpvariabler tar sina värden oberoende av varandra eller inte, eller om värdet av den ena har ett samband med värdet av den andra. Hypoteserna kommer alltså att uttryckas i ord, inte i matematiska symboler. Vi bygger upp diskussionen kring följande exempel:
Det finns en teori om att könet på ett barn i livmodern är relaterat till barnets hjärtfrekvens: småflickor tenderar att ha högre hjärtfrekvens. Anta att vi vill testa denna teori. Vi undersöker hjärtfrekvensregistreringarna för 40 bebisar som togs under deras mödrars sista prenatala kontroller före förlossningen, och för var och en av dessa 40 slumpmässigt utvalda registreringar beräknar vi värdena för två slumpmässiga mått: 1) kön och 2) hjärtfrekvens. I detta sammanhang kallas dessa två slumpmässiga mått ofta för faktorer En variabel med flera kvalitativa nivåer … Eftersom bevisbördan är att hjärtfrekvens och kön är relaterade, inte att de är orelaterade, kan problemet med att testa teorin om barnets kön och hjärtfrekvens formuleras som ett test av följande hypoteser:
H0:Barnets kön och barnets hjärtfrekvens är oberoendevs. Ha:Barnets kön och barnets hjärtfrekvens är inte oberoende
Fakten kön har två naturliga kategorier eller nivåer: pojke och flicka. Vi delar upp den andra faktorn, hjärtfrekvens, i två nivåer, låg och hög, genom att välja en viss hjärtfrekvens, till exempel 145 slag per minut, som gräns mellan dem. En hjärtfrekvens under 145 slag per minut betraktas som låg och 145 och högre som hög. De 40 registreringarna ger upphov till en 2 × 2-kontingenstabell. Genom att lägga samman rad- och kolumntotaler samt en totalsumma får vi tabellen som visas i tabell 11.1 ”Baby Gender and Heart Rate”. De fyra posterna i fetstil är antal observationer från urvalet n = 40. Det fanns 11 flickor med låg hjärtfrekvens, 17 pojkar med låg hjärtfrekvens och så vidare. De utgör kärnan i den utökade tabellen.
Tabell 11.1 Barnens kön och hjärtfrekvens
| Hjärtfrekvens | ||||
|---|---|---|---|---|
| Låg | Hög | Rad totalt | ||
| Genus | Flicka | 11 | 7 | 18 |
| Pojke | 17 | 5 | 22 | |
| Skolumn totalt | 28 | 12 | Total = 40 | |
I analogi med det faktum att sannolikheten för oberoende händelser är produkten av sannolikheterna för varje händelse, Om hjärtfrekvens och kön var oberoende skulle vi förvänta oss att antalet i varje kärncell skulle vara nära produkten av radantalet R och kolumnantalet C för den rad och kolumn som innehåller den, dividerat med urvalsstorleken n. Om vi kallar ett sådant förväntat antal observationer E är dessa fyra förväntade värden:
- 1:a raden och 1:a kolumnen: E=(R×C)∕n=18×28∕40=12,6
- 1:a raden och 2:a kolumnen: E=(R×C)∕n=18×12∕40=5,4
- 2:a raden och 1:a kolumnen: E=(R×C)∕n=22×28∕40=15,4
- 2:a raden och andra kolumnen: E=(R×C)∕n=22×12∕40=6,6
Vi uppdaterar tabell 11.1 ”Barnets kön och hjärtfrekvens” genom att placera varje förväntat värde i sin motsvarande kärncell, precis under det observerade värdet i cellen. Detta ger den uppdaterade tabellen Tabell 11.2 ”Uppdaterat kön och hjärtfrekvens för barn”.
Tabell 11.2 Uppdaterat kön och hjärtfrekvens
| Hjärtfrekvens | ||||
|---|---|---|---|---|
| Låg | Hög | Rad totalt | ||
| Genus | Flicka | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Pojke | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Kolonnsumma | C = 28 | C = 12 | n = 40 | |
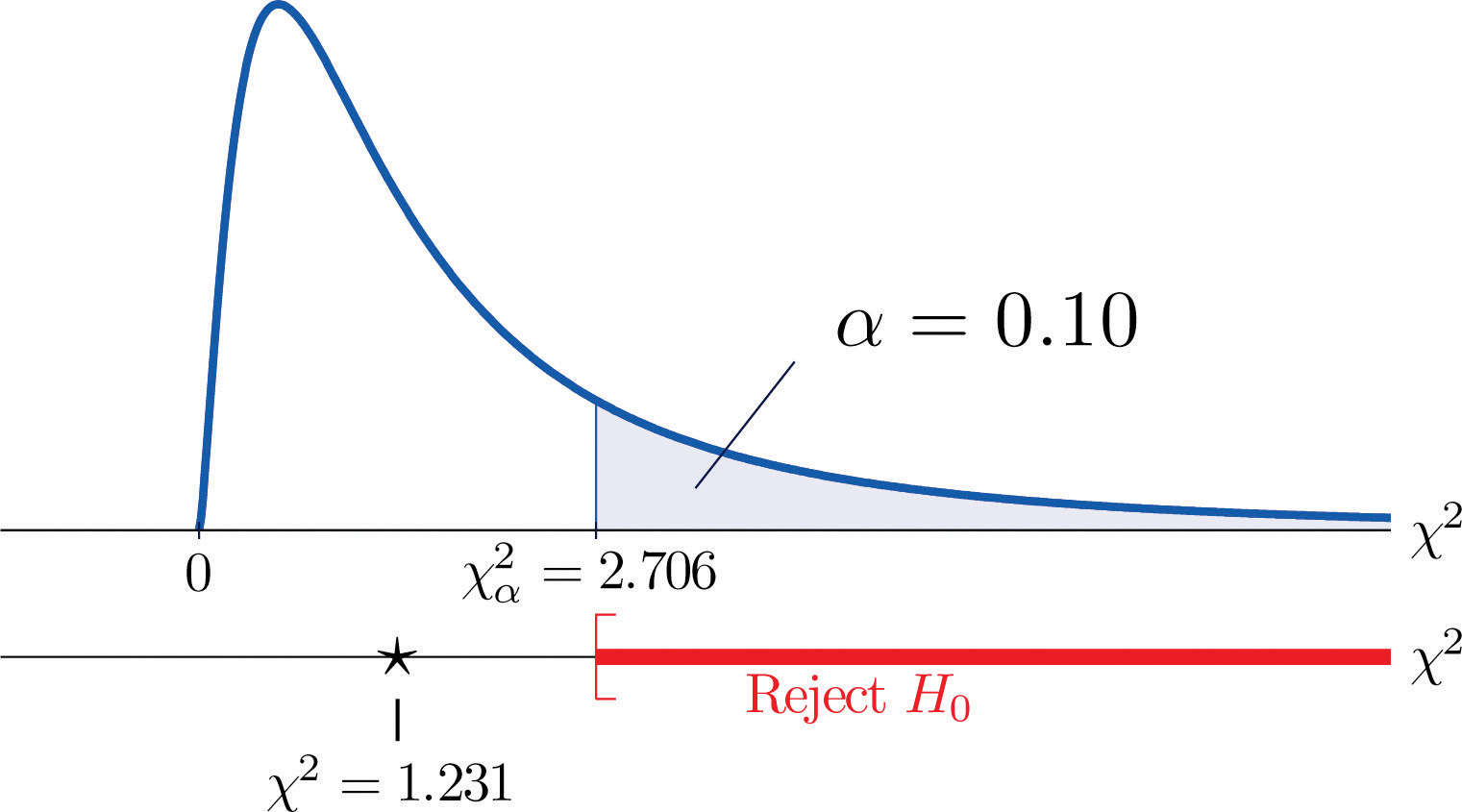
Ett mått på hur mycket data avviker från vad vi skulle förvänta oss att se om faktorerna verkligen var oberoende är summan av kvadraterna på skillnaden mellan talen i varje kärncell, eller, genom att standardisera genom att dividera varje kvadrat med det förväntade antalet i cellen, summan Σ(O-E)2∕E. Vi skulle förkasta nollhypotesen att faktorerna är oberoende endast om detta tal är stort, så testet är högerhaltigt. I det här exemplet har slumpvariabeln Σ(O-E)2∕E chi-två-fördelningen med en frihetsgrad. Om vi från början hade beslutat att testa på 10 % signifikansnivå skulle det kritiska värdet som definierar förkastningsområdet vara, enligt figur 12.4 ”Critical Values of Chi-Square Distributions”, χα2=χ0,102=2,706, så att förkastningsområdet skulle vara intervallet [2,706,∞). När vi beräknar värdet av den standardiserade teststatistiken får vi
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Då 1,231 < 2,706, är beslutet att inte förkasta H0. Se figur 11.3 ”Förutsägelse av barnets kön”. Uppgifterna ger inte tillräckliga bevis, på 10 procents signifikansnivå, för att dra slutsatsen att hjärtfrekvens och kön är relaterade.
Figur 11.3 Förutsägelse av kön hos bebisar
Med detta specifika exempel i åtanke, övergår vi nu till den allmänna situationen. I den allmänna inställningen att testa oberoende av två faktorer, kalla dem faktor 1 och faktor 2, är de hypoteser som ska testas
H0:De två faktorerna är oberoendevs. Ha:De två faktorerna är inte oberoende
Som i exemplet är varje faktor indelad i ett antal kategorier eller nivåer. Dessa kan uppstå naturligt, som i uppdelningen pojke-flicka av kön, eller något godtyckligt, som i uppdelningen hög-låg av hjärtfrekvens. Anta att faktor 1 har I-nivåer och faktor 2 har J-nivåer. Då ger informationen från ett slumpmässigt urval upphov till en allmän I × J-kontingenstabell, som med radsummor, kolumnsummor och en totalsumma skulle se ut som i tabell 11.3 ”Allmän kontingenstabell”. Varje cell kan märkas med ett par index (i,j). Oij står för det observerade antalet observationer i cellen i rad i och kolumn j, Ri för den i:e radsumman och Cj för den j:e kolumnsumman. För att förenkla notationen släpper vi indexen så att tabell 11.3 ”Allmän eventualitetstabell” blir tabell 11.4 ”Förenklad allmän eventualitetstabell”. Det är dock viktigt att komma ihåg att Os, Rs och Cs, även om de betecknas med samma symboler, i själva verket är olika tal.
Tabell 11.3 Allmänt om oförutsedda händelser
| Faktor 2 Nivåer | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Rad totalt | ||
| Faktor 1 Nivåer | 1 | O11 | – – – | O1j | – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – – | Oij | – – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OI1 | – – – – | OIj | – – – – | OIJ | RI | |
| Skolumn totalt | C1 | – – – – | Cj | – – – – | CJ | n | |
Tabell 11.4 Förenklad tabell för allmänna oförutsedda händelser
| Faktor 2-nivåer | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Rad totalt | |||
| Faktor 1 Nivåer | 1 | O | – – – | O | – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – – | O | – – – – | O | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | O | – – – – | O | – – – – | O | R | ||
| Skolumn totalt | C | – – – – | C | – – – | C | n | ||
Som i exemplet, För varje kärncell i tabellen beräknar vi vad som skulle vara det förväntade antalet E observationer om de två faktorerna var oberoende. E beräknas för varje kärncell (varje cell med ett O i den) i tabell 11.4 ”Simplified General Contingency Table” med hjälp av den regel som tillämpades i exemplet:
där R är raktotalen och C är kolonntotalen som motsvarar cellen, och n är urvalsstorleken.
När det förväntade antalet har beräknats för varje cell uppdateras tabell 11.4 ”Förenklad allmän eventualitetstabell” till tabell 11.5 ”Uppdaterad allmän eventualitetstabell” genom att det beräknade värdet av E infogas i varje kärncell.
Tabell 11.5 Uppdaterad tabell över allmänna oförutsedda händelser
| Faktor 2-nivåer | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – – | J | Rad totalt | |||
| Faktor 1 Nivåer | 1 | OE | – – – | OE | – – – | OE | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| i | OE | – – – – | OE | – – – – | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – – – | OE | – – – – | OE | R | ||
| Skolumnsumma | C | – – – | C | – – – | C | n | ||
Här är teststatistiken för den allmänna hypotesen baserad på tabell 11.5 ”Updated General Contingency Table”, tillsammans med villkoren att den följer en chi-square-fördelning.
Teststatistik för test av två faktorers oberoende
χ2=Σ(O-E)2E
där summan är över alla kärnceller i tabellen.
Om
- de två undersökningsfaktorerna är oberoende, och
- det observerade antalet O för varje cell i tabell 11.5 ”Uppdaterad allmän kontingenstabell” är minst 5,
då följer χ2 ungefärligen en chi-två-fördelning med df=(I-1)×(J-1) frihetsgrader.
Samma femstegsförfaranden, antingen det kritiska värdet eller p-värdet, som introducerades i avsnitt 8.1 ”Elementen i hypotesprövning” och avsnitt 8.3 ”Den observerade betydelsen av ett test” i kapitel 8 ”Prövning av hypoteser”, används för att utföra testet, som alltid är högerstjärtad.
Exempel 1
En forskare vill undersöka om elevernas resultat på ett inträdesprov till en högskola (CEE) har någon indikativ kraft för framtida prestationer på högskolan som mäts med GPA. Med andra ord vill han undersöka om faktorerna CEE och GPA är oberoende eller inte. Han väljer slumpmässigt ut n = 100 studenter på en högskola och noterar varje students resultat på inträdesprovet och hans betygsgenomsnitt i slutet av andra året. Han delar in poäng på inträdesprovet i två nivåer och betygsgenomsnittet i tre nivåer. Genom att sortera uppgifterna i enlighet med dessa indelningar bildar han en tillfällighetstabell som visas i tabell 11.6 ”CEE versus GPA Contingency Table”, där rad- och kolumnsummorna redan har beräknats.
Tabell 11.6 CEE kontra GPA Contingency Table
| GPA | |||||
|---|---|---|---|---|---|
| <2,7 | 2,7 till 3,2 | >3.2 | Rad Totalt | ||
| CEE | 1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Skolumnsumma | 41 | 36 | 23 | Total=100 | |
Test, på 1 procents signifikansnivå, om dessa uppgifter ger tillräckliga bevis för att man ska kunna dra slutsatsen att CEE-poäng indikerar framtida prestationsnivåer för inkommande nybörjare på högskolor som mäts med hjälp av GPA.
Lösning:
Vi utför testet med hjälp av metoden med kritiskt värde och följer den vanliga femstegsmetoden som beskrivs i slutet av avsnitt 8.1 ”Elementen i hypotesprövning” i kapitel 8 ”Prövning av hypoteser”.
-
Steg 1. Hypoteserna är
H0:CEE och GPA är oberoende faktorer vs. Ha:CEE och GPA är inte oberoende faktorer
- Steg 2. Fördelningen är chi-square.
-
Steg 3. För att beräkna värdet av teststatistiken måste vi först beräkna det förväntade antalet för var och en av de sex kärncellerna (de vars poster är fetstilade):
- 1:a raden och 1:a kolumnen: E=(R×C)∕n=41×52∕100=21,32
- 1:a raden och 2:a kolumnen: E=(R×C)∕n=36×52∕100=18,72
- 1:a raden och 3:e kolumnen: E=(R×C)∕n=23×52∕100=11,96
- 2:a raden och 1:a kolumnen: E=(R×C)∕n=41×48∕100=19,68
- 2:a raden och andra kolumnen: E=(R×C)∕n=36×48∕100=17.28
- 2:a raden och 3:e kolumnen: E=(R×C)∕n=23×48∕100=11,04
Tabell 11.6 ”CEE versus GPA Contingency Table” har uppdaterats till tabell 11.7 ”Updated CEE versus GPA Contingency Table”.
Tabell 11.7 Uppdaterad CEE- och GPA-tabell
GPA <2.7 2.7 2.7 till 3.2 >3.2 Rad totalt CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Skolumn totalt C = 41 C = 36 C = 23 n = 100 Teststatistiken är
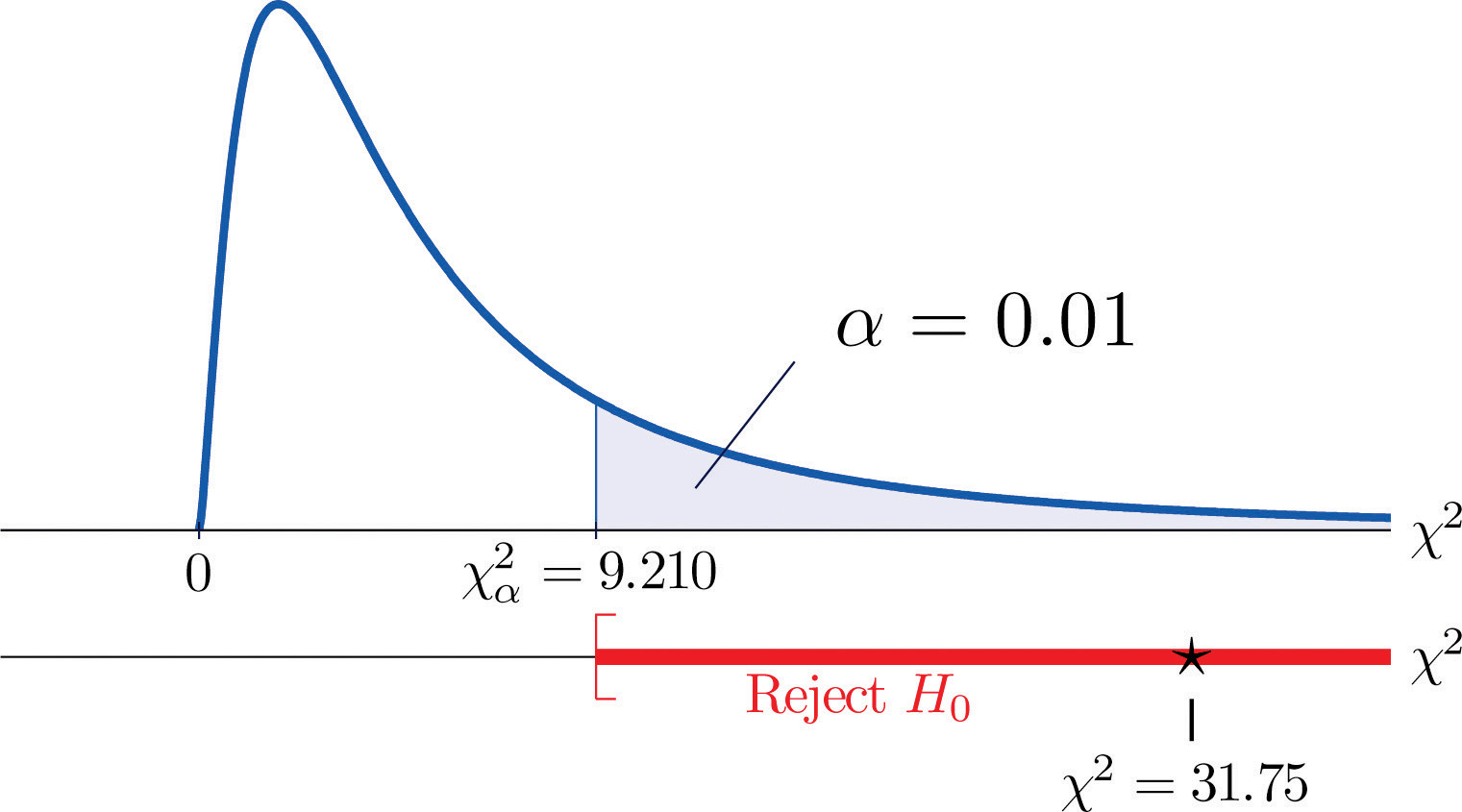
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Eftersom CEE-faktorn har två nivåer och GPA-faktorn har tre, är I = 2 och J = 3. Teststatistiken följer således chi-square-fördelningen med df=(2-1)×(3-1)=2 frihetsgrader.
Då testet är rättsvansat är det kritiska värdet χ0,012. När man läser från figur 12.4 ”Critical Values of Chi-Square Distributions” är χ0,012=9,210, så förkastningsområdet är [9,210,∞).
- Steg 5. Eftersom 31,75 > 9,21 är beslutet att förkasta nollhypotesen. Se figur 11.4. Uppgifterna ger tillräckliga bevis, på signifikansnivån 1 %, för att dra slutsatsen att CEE-poängen och GPA inte är oberoende: Poängen på inträdesprovet har en prediktiv förmåga.
Figur 11.4 Anmärkning 11.9 ”Exempel 1”
Nyckelkunskaper
- Kritiska värden för en chi-två-fördelning med frihetsgrader df återfinns i figur 12.4 ”Critical Values of Chi-Square Distributions”.
- Ett chi-två-testEtt test baserat på en chi-två-statistik för att kontrollera om två faktorer är oberoende. kan användas för att utvärdera hypotesen att två slumpmässiga variabler eller faktorer är oberoende.
Övningar
-
Hitta χ0,012 för vart och ett av följande antal frihetsgrader.
- df=5
- df=11
- df=25
-
Hitta χ0,052 för vart och ett av följande antal frihetsgrader.
- df=6
- df=12
- df=30
-
Finn χ0.102 för vart och ett av följande antal frihetsgrader:
- df=6
- df=12
- df=30
-
Hitta χ0.012 för vart och ett av följande antal frihetsgrader:
- df=7
- df=10
- df=20
-
För df=7 och α=0.05, hitta
- χα2
- χα22
-
För df=17 och α=0.01, hitta
- χα2
- χα22
-
Ett dataurval sorteras in i en 2 × 2 kontingenstabell baserad på två faktorer som var och en har två nivåer.
Faktor 1 Nivå 1 Nivå 2 Rad totalt Faktor 2 Nivå 1 20 10 R Nivå 2 15 5 R Kolonnsumma C C n - Hitta kolonnsumman, radarnas totalsumma och totalsumman n för tabellen.
- Finn det förväntade antalet E observationer för varje cell baserat på antagandet att de två faktorerna är oberoende (det vill säga använd bara formeln E=(R×C)∕n).
- Finn värdet av chi-square-teststatistiken χ2.
- Hitta antalet frihetsgrader för chi-square-teststatistiken.
-
Ett dataurval sorteras in i en 3 × 2 contingencytabell baserat på två faktorer, varav den ena har tre nivåer och den andra två nivåer.
Faktor 1 Nivå 1 Nivå 2 .
Rad totalt Faktor 2 Nivå 1 20 10 R Nivå 2 15 5 R Nivå 3 10 20 R R Kolonnsumma C C n - Hitta kolonnsumman, radarnas totalsumma och totalsumman n för tabellen.
- Finn det förväntade antalet E observationer för varje cell baserat på antagandet att de två faktorerna är oberoende (det vill säga använd bara formeln E=(R×C)∕n).
- Finn värdet av chi-square-teststatistiken χ2.
- Hitta antalet frihetsgrader för chi-square-teststatistiken.
Grundläggande
-
En barnpsykolog anser att barn presterar bättre på prov när de ges en upplevd valfrihet. För att testa denna tro genomförde psykologen ett experiment där 200 tredjeklassare slumpmässigt fördelades på två grupper, A och B. Varje barn fick samma enkla logiska test. Men i grupp B fick varje barn friheten att välja ett texthäfte bland många med olika teckningar på omslagen. Varje barns prestation bedömdes som mycket bra, bra och ganska bra. Resultaten sammanfattas i tabellen. Testa, med en signifikansnivå på 5 %, om det finns tillräckliga bevis i uppgifterna för att stödja psykologens uppfattning.
Grupp A B Prestation Varligt bra 32 29 .
Good 55 61 Fair 10 13
Användningar
Med avseende på tävlingar i vinprovning, Många experter hävdar att det första glaset vin som serveras ger en referenssmak och att ett annat referensvin kan ändra den relativa rangordningen av de andra vinerna i tävlingen. För att testa detta påstående serverades tre viner, A, B och C, vid en vinprovning. Varje person serverades ett enda glas av varje vin, men i olika ordning för olika gäster. Vid avslutningen ombads varje person att nämna det bästa av de tre vinerna. Det var 172 personer som deltog i evenemanget och deras bästa val anges i tabellen. Testa, på 1 % signifikansnivå, om det finns tillräckliga bevis i uppgifterna för att stödja påståendet att vinexperternas preferenser är beroende av det först serverade vinet.
| Toppval | ||||
|---|---|---|---|---|
| A | B | C | ||
| Första glas | A | 12 | 31 | 27 |
| B | 15 | 40 | 21 | |
| C | 10 | 9 | 7 | |
Vi lämnar-är ärftlig? För att besvara denna fråga väljs 250 vuxna slumpmässigt ut och deras och deras föräldrars handledighet noteras. Resultaten sammanfattas i tabellen. Testa, med en signifikansnivå på 1 %, om det finns tillräckliga bevis i uppgifterna för att dra slutsatsen att det finns ett ärftligt inslag i handfallenhet.
| Antal föräldrar vänsterhänt-Handed | ||||
|---|---|---|---|---|
| 0 | 1 | 2 | ||
| Handedness | Left | 8 | 10 | 12 |
| Högre | 178 | 21 | 21 | |
Vissa genetiker hävdar att de gener som bestämmer vänster-handledighet också styr utvecklingen av hjärnans språkcentrum. Om detta påstående är sant skulle det vara rimligt att förvänta sig att vänsterhänta personer tenderar att ha starkare språkförmåga. I en studie som utformades för att testa detta påstående valdes 807 studenter slumpmässigt ut som gjorde Graduate Record Examination (GRE). Deras poäng på språkdelen av provet klassificerades i tre kategorier: låg, genomsnittlig och hög, och deras handstil noterades också. Resultaten redovisas i den bifogade tabellen. Testa, med en signifikansnivå på 5 %, om det finns tillräckliga bevis i uppgifterna för att dra slutsatsen att vänsterhänta personer tenderar att ha en starkare språkförmåga.
| GRE English Scores | ||||
|---|---|---|---|---|
| Low | Average | Hög | ||
| Handledighet | Vänster | 18 | 40 | 22 |
| Högre | 201 | 360 | 166 | |
Det anses allmänt att barn som växer upp i stabila familjer tenderar att klara sig bra i skolan. För att verifiera en sådan uppfattning undersökte en samhällsvetare 290 slumpmässigt utvalda elevers journaler i en offentlig gymnasieskola och noterade varje elevs familjestruktur och akademiska status fyra år efter att de börjat gymnasiet. Uppgifterna sorterades sedan in i en 2 × 3-kontingenstabell med två faktorer. Faktor 1 har två nivåer: avslutade studier och inte avslutade studier. Faktor 2 har tre nivåer: ingen förälder, en förälder och två föräldrar. Resultaten anges i den bifogade tabellen. Testa, med en signifikansnivå på 1 %, om det finns tillräckliga bevis i uppgifterna för att dra slutsatsen att familjestrukturen har betydelse för elevernas skolprestationer.
| Akademisk status | |||
|---|---|---|---|
| Graduated | Did Not Graduate | ||
| Familj | Ingen förälder | 18 | 31 |
| En förälder | 101 | 44 | |
| Två föräldrar | 70 | 26 | |
En administratör på en stor mellanstadieskola vill använda sig av kändisars inflytande för att uppmuntra eleverna att göra hälsosammare val i skolans cafeteria. Cafeterian ligger i mitten av ett öppet område. Varje dag vid lunchtid får eleverna sin lunch och en dryck i tre separata rader som leder till tre separata serveringsstationer. Som ett experiment visade skoladministratören en affisch med en populär tonårspopstjärna som dricker mjölk vid vart och ett av de tre ställena där drycker serveras, förutom att mjölken på affischen är olika vid varje ställe: en visar vit mjölk, en visar rosa mjölk med jordgubbssmak och en visar chokladmjölk. Efter experimentets första dag noterade administratören elevernas mjölkval separat för de tre linjerna. Uppgifterna finns i den bifogade tabellen. Testa, på 1 % signifikansnivå, om det finns tillräckliga bevis i uppgifterna för att dra slutsatsen att affischerna hade en viss inverkan på elevernas val av dryck.
| Student Choice | ||||
|---|---|---|---|---|
| Regular | Strawberry | Chocolate | ||
| Poster Choice | ||||
| Regular | 38 | 28 | 40 | |
| Strawberry | 18 | 18 | 51 | 24 |
| Choklad | 32 | 32 | 53 | |
-
Large Uppgiftsuppsättning 8 innehåller resultatet av en undersökning av 300 slumpmässigt utvalda vuxna som regelbundet går på bio. För varje person registrerades kön och önskad typ av film. Testa, med en signifikansnivå på 5 %, om det finns tillräckliga bevis i uppgifterna för att dra slutsatsen att faktorerna ”kön” och ”föredragen typ av film” är beroende.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Large Uppgiftsuppsättning Övning
Svar
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5.99, förkastar inte H0
-
χ2=72.35, χ0.012=9.21, förkastar H0
-
χ2=21.2784, χ0.012=9.21, förkasta H0
-
χ2=28.4539. df=3. Förkastningsområde: [7.815,∞). Beslut: Förkastar H0 om oberoende.
.