Testes para Independência
Testes de Hipóteses encontrados anteriormente no livro tinham a ver com a forma como os valores numéricos de dois parâmetros populacionais eram comparados. Nesta subsecção vamos investigar hipóteses que têm a ver com se duas variáveis aleatórias tomam ou não os seus valores independentemente, ou se o valor de uma tem uma relação com o valor da outra. Assim, as hipóteses serão expressas em palavras e não em símbolos matemáticos. Construímos a discussão em torno do seguinte exemplo.
Há uma teoria de que o sexo de um bebé no útero está relacionado com a frequência cardíaca do bebé: as meninas tendem a ter uma frequência cardíaca mais elevada. Suponha que desejamos testar esta teoria. Examinamos os registros de freqüência cardíaca de 40 bebês tomados durante os últimos exames pré-natais de suas mães antes do parto, e para cada um desses 40 registros selecionados aleatoriamente calculamos os valores de duas medidas aleatórias: 1) o sexo e 2) a frequência cardíaca. Neste contexto, estas duas medidas aleatórias são muitas vezes chamadas de factoresA variável com vários níveis qualitativos. Como o ónus da prova é que a frequência cardíaca e o sexo estão relacionados e não que não estejam relacionados, o problema de testar a teoria sobre o sexo e frequência cardíaca do bebé pode ser formulado como um teste das seguintes hipóteses:
H0:O sexo e a frequência cardíaca do bebé são independentesvs. Ha:O sexo e a frequência cardíaca do bebé não são independentes
O factor género tem duas categorias ou níveis naturais: rapaz e rapariga. Nós dividimos o segundo fator, freqüência cardíaca, em dois níveis, baixo e alto, escolhendo algumas batidas cardíacas, digamos 145 batidas por minuto, como o corte entre eles. Uma freqüência cardíaca abaixo de 145 batimentos por minuto será considerada baixa e 145 e acima será considerada alta. Os 40 registros dão origem a uma tabela de contingência de 2 × 2. Por totais de linhas adjacentes, totais de colunas e um total geral, obtemos a tabela mostrada como a Tabela 11.1 “Gênero Bebê e Freqüência Cardíaca”. Os quatro registros em negrito são contagens de observações da amostra de n = 40. Havia 11 meninas com freqüência cardíaca baixa, 17 meninos com freqüência cardíaca baixa, e assim por diante. Eles formam o núcleo da tabela expandida.
Tabela 11.1 Sexo Bebê e freqüência cardíaca
| Ritmo cardíaco | ||||
|---|---|---|---|---|
| Baixo | Alto | Row Total | ||
| Gênero | Girl | 11 | 7 | 18 |
| Boy | 17 | 5 | 22 | |
| Coluna Total | 28 | 12 | Total = 40 | |
Em analogia com o fato de que a probabilidade de eventos independentes é o produto das probabilidades de cada evento, Se a frequência cardíaca e o sexo fossem independentes, então esperaríamos que o número em cada célula central estivesse próximo do produto da linha total R e coluna total C da linha e coluna que a contém, dividido pelo tamanho da amostra n. Denotando esse número esperado de observações E, esses quatro valores esperados são:
- 1ª linha e 1ª coluna: E=(R×C)∕n=18×28∕40=12,6
- 1ª linha e 2ª coluna: E=(R×C)∕n=18×12∕40=5,4
- 2ª linha e 1ª coluna: E=(R×C)∕n=18×12∕40=5,4
- 2ª linha e 1ª coluna: E=(R×C)∕n=22×28∕40=15,4
- 2ª linha e 2ª coluna: E=(R×C)∕n=22×28∕40=15,4
- 2ª linha e 2ª coluna: E=(R×C)∕n=22×12∕40=6,6
Atualizamos a tabela 11.1 “Gênero e freqüência cardíaca do bebê” colocando cada valor esperado em sua célula central correspondente, bem abaixo do valor observado na célula. Isto dá a tabela actualizada Tabela 11.2 “Género Bebé e Frequência Cardíaca Actualizada”.
Tabela 11.2 Gênero e freqüência cardíaca do bebê atualizados
| Ritmo cardíaco | ||||
|---|---|---|---|---|
| Baixo | Alto | Row Total | ||
| Gênero | Rapariga | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Boy | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Coluna Total | C = 28 | C = 12 | n = 40 | |
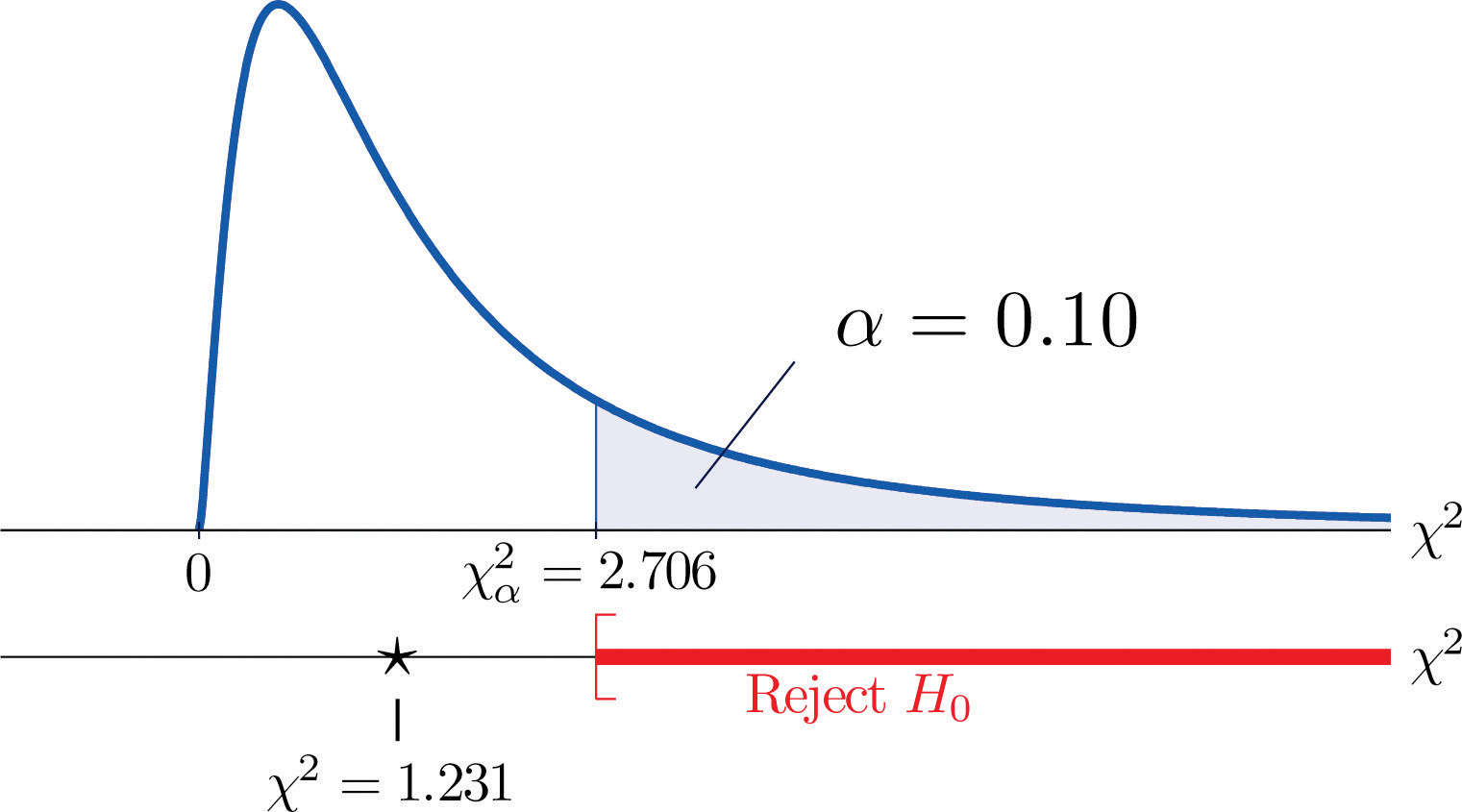
Uma medida de quanto os dados se desviam do que esperaríamos ver se os fatores realmente eram independentes é a soma dos quadrados da diferença dos números em cada célula central, ou, padronizando, dividindo cada quadrado pelo número esperado na célula, a soma Σ(O-E)2∕E. Rejeitaríamos a hipótese nula de que os fatores são independentes apenas se esse número for grande, de modo que o teste é direito-detalhado. Neste exemplo, a variável aleatória Σ(O-E)2∕E tem a distribuição qui-quadrado com um grau de liberdade. Se tivéssemos decidido no início testar ao nível de 10% de significância, o valor crítico que define a região de rejeição seria, lendo da Figura 12.4 “Valores Críticos das Distribuições Qui-quadrado”, χα2=χ0.102=2.706, de forma que a região de rejeição seria o intervalo [2.706,∞). Quando calculamos o valor da estatística do teste padronizado obtemos
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Desde 1,231 < 2,706, a decisão é não rejeitar o H0. Ver Figura 11.3 “Baby Gender Prediction”. Os dados não fornecem evidências suficientes, ao nível de 10% de significância, para concluir que a frequência cardíaca e o sexo estão relacionados.
Figure 11.3 Baby Gender Prediction
Com este exemplo específico em mente, agora vire-se para a situação geral. No cenário geral de testar a independência de dois fatores, chame-os de Fator 1 e Fator 2, as hipóteses a serem testadas são
H0:Os dois fatores são independentesvs. Ha:Os dois fatores não são independentes
Como no exemplo, cada fator é dividido em várias categorias ou níveis. Estes podem surgir naturalmente, como na divisão rapaz-mulher do sexo, ou de forma algo arbitrária, como na divisão rapaz-baixo da frequência cardíaca. Suponha que o Fator 1 tem níveis I e o Fator 2 tem níveis J. Então a informação de uma amostra aleatória dá origem a uma tabela geral de contingência I × J, que com totais de linhas, totais de colunas e um total geral apareceria como mostrado na Tabela 11.3 “Tabela Geral de Contingência”. Cada célula pode ser rotulada por um par de índices (i,j). Oij significa a contagem observada de observações na célula na linha i e coluna j, Ri para o total da linha i e Cj para o total da coluna j. Para simplificar a notação vamos deixar cair os índices de modo que a Tabela 11.3 “Tabela de Contingência Geral” se torna a Tabela 11.4 “Tabela de Contingência Geral Simplificada”. No entanto é importante ter em mente que os Os, os Rs e os Cs, embora denotados pelos mesmos símbolos, são na verdade números diferentes.
Tabela 11.3 Tabela de Contingência Geral
| Factor 2 Níveis | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Total de linhas | ||
| Factor 1 Níveis | 1 | O11 | – – – – – | O1j | – – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – – | Oij | – – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| I | OI1 | – – – | OIj | – – – – – | OIJ | RI | |
| Total da coluna | C1 | – – – – | Cj | – – – – – | CJ | n | |
Quadro 11.4 Tabela de Contingência Geral Simplificada
| Factor 2 Níveis | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Total de linha | ||
| Factor 1 Níveis | 1 | O | – – – – | O | – – – – | O | >R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | O | – – – – – | O | – – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| I | O | – – – | O | – – – – | O | R | |
| Total da coluna | C | – – – | C | – – – – | C | n | |
As no exemplo, para cada célula central da tabela, calculamos qual seria o número E esperado de observações se os dois fatores fossem independentes. E é calculado para cada célula central (cada célula com um O dentro) da Tabela 11.4 “Tabela Simplificada de Contingência Geral” pela regra aplicada no exemplo:
onde R é o total da linha e C é o total da coluna correspondente à célula, e n é o tamanho da amostra.
Após o número esperado ser calculado para cada célula, a Tabela 11.4 “Tabela Simplificada de Contingência Geral” é atualizada para formar a Tabela 11.5 “Tabela de Contingência Geral Atualizada”, inserindo o valor calculado de E em cada célula núcleo.
Tabela 11.5 Tabela de Contingência Geral Atualizada
| Fator 2 Níveis | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – – | J | Total de linhas | ||
| Factor 1 Níveis | 1 | OE | – – – – | OE | – – – – | OE | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | OE | – – – – | OE | – – – – | OE | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – – – | OE | – – – | OE | R | |
| Coluna Total | C | – – – – | C | – – | C | n | |
Aqui está a estatística do teste para a hipótese geral baseada na Tabela 11.5 “Tabela de Contingência Geral Atualizada”, juntamente com as condições de que ela segue uma distribuição qui-quadrada.
Test statistic for Testing the Independence of Two Factors
χ2=Σ(O-E)2E
onde a soma está sobre todas as células centrais da tabela.
Se
- os dois fatores de estudo são independentes, e
- a contagem O observada de cada célula da Tabela 11.5 “Tabela de Contingência Geral Atualizada” é de pelo menos 5,
então χ2 aproximadamente segue uma distribuição qui-quadrada com df=(I-1)×(J-1) graus de liberdade.
Os mesmos procedimentos de cinco passos, ou a abordagem do valor crítico ou a abordagem do valor p, que foram introduzidos na Secção 8.1 “Os Elementos do Teste de Hipóteses” e Secção 8.3 “A Significância Observada de um Teste” do Capítulo 8 “Testar Hipóteses” são usados para realizar o teste, que é sempre de cauda direita.
Exemplo 1
Um pesquisador deseja investigar se os resultados dos estudantes em um exame de admissão (CEE) têm algum poder indicativo para o desempenho futuro da faculdade, conforme medido pelo GPA. Em outras palavras, ele deseja investigar se os fatores CEE e GPA são independentes ou não. Ele seleciona aleatoriamente n = 100 alunos de uma faculdade e anota a nota de cada aluno no exame de admissão e sua média de notas no final do segundo ano. Ele divide as notas no exame de admissão em dois níveis e as médias de notas em três níveis. Ordenando os dados de acordo com essas divisões, ele forma a tabela de contingência mostrada como Tabela 11.6 “CEE versus Tabela de Contingência de GPA”, na qual os totais das linhas e colunas já foram computados.
Tabela 11.6 “CEE versus GPA Tabela de Contingência
| GPA | |||||
|---|---|---|---|---|---|
| <2.7 | 2.7 a 3.2 | >>3.2 | Total de linha | ||
| CEE | <1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Coluna Total | 41 | 36 | 23 | Total=100 | |
Teste, no nível de 1% de significância, se esses dados fornecem evidências suficientes para concluir que as pontuações da CEE indicam níveis futuros de desempenho dos calouros universitários entrantes, conforme medido pelo GPA.
Solução:
Realizamos o teste usando a abordagem do valor crítico, seguindo o método usual de cinco passos delineado no final da Seção 8.1 “Os Elementos do Teste de Hipóteses” no Capítulo 8 “Testando Hipóteses”.
-
Passo 1. As hipóteses são
H0:CEE e GPA são fatores independentessvs. Ha:CEE e GPA não são fatores independentes
- Passo 2. A distribuição é qui-quadrado.
-
Passo 3. Para calcular o valor da estatística do teste devemos primeiro calcular o número esperado para cada uma das seis células centrais (aquelas cujas entradas estão em negrito):
- 1ª linha e 1ª coluna: E=(R×C)∕n=41×52∕100=21,32
- 1ª fila e 2ª coluna: E=(R×C)∕n=36×52∕100=18,72
- 1ª fila e 3ª coluna: E=(R×C)52∕100=36×52∕100=18,72
- 1ª fila e 3ª coluna: E=(R×C)∕n=23×52∕100=11,96
- 2ª fila e 1ª coluna: E=(R×C)52∕100=23×52∕100=11,96
- 2ª fila e 1ª coluna: E=(R×C)∕n=41×48∕100=19,68
- 2ª linha e 2ª coluna: E=(R×C)48∕100=41×48∕100=19,68
- 2ª linha e 2ª coluna: E=(R×C)∕n=36×48∕100=17,28
- 2ª linha e 3ª coluna: E=(R×C)48∕100=36×48∕100=17,28
- 2ª linha e 3ª coluna: E=(R×C)∕n=23×48∕100=11.04
Tabela 11.6 “Tabela CEE versus GPA Contingency Table” é atualizada para a Tabela 11.7 “Tabela CEE versus GPA Contingency Table”.
Tabela 11.7 “Tabela de CEE versus GPA de Contingência”.
GPA <2,7 2.7 a 3,2 >3,2 Total de linhas CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Total da coluna C = 41 C = 36 C = 23 n = 100 A estatística do teste é
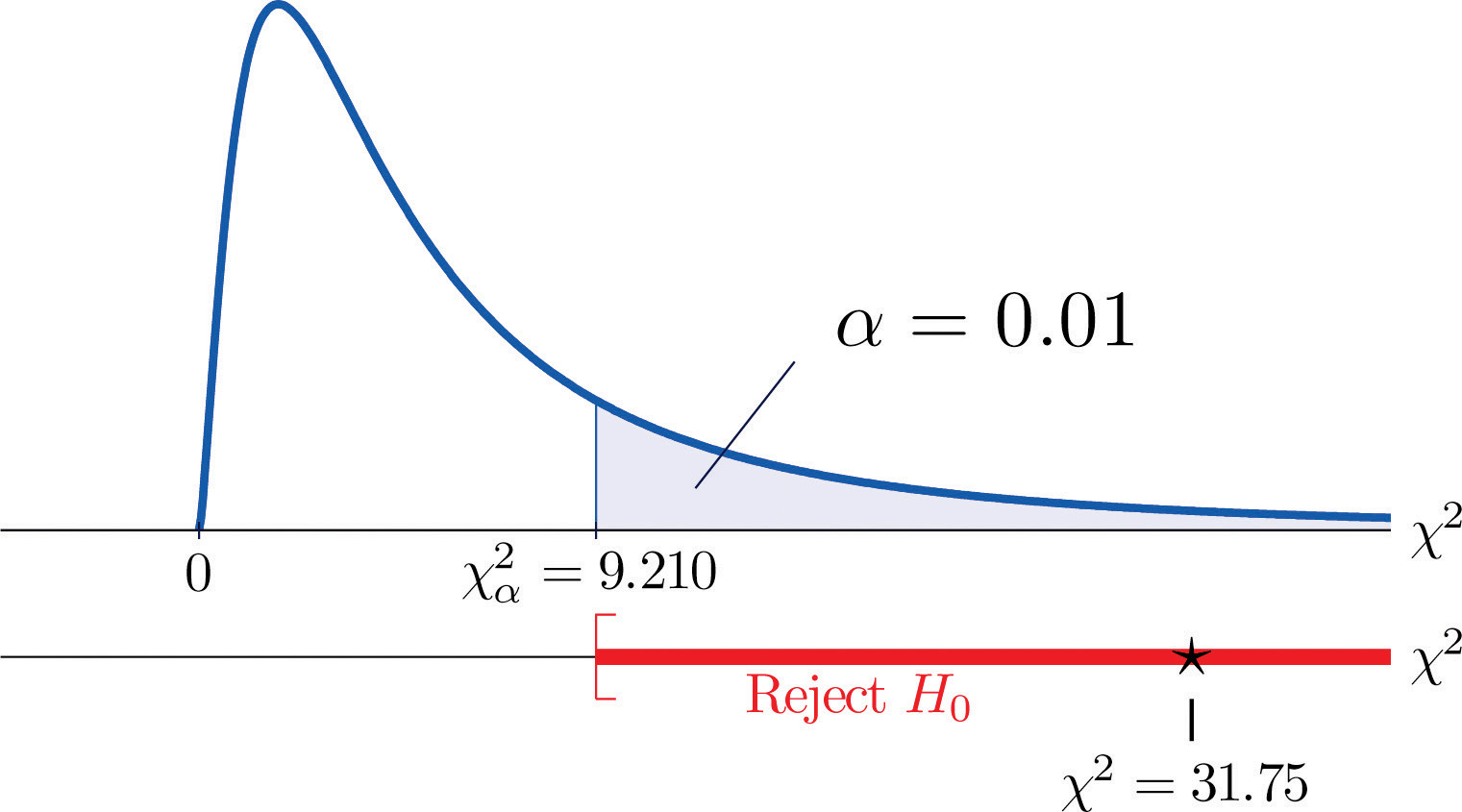
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Como o fator CEE tem dois níveis e o fator GPA tem três, I = 2 e J = 3. Assim, a estatística do teste segue a distribuição qui-quadrado com df=(2-1)×(3-1)=2 graus de liberdade.
Desde que o teste seja de cauda direita, o valor crítico é χ0.012. Lendo da Figura 12.4 “Valores Críticos das Distribuições Qui-quadradas”, χ0.012=9.210, então a região de rejeição é [9.210,∞).
- Passo 5. Desde 31,75 > 9,21 a decisão é de rejeitar a hipótese nula. Veja a Figura 11.4. Os dados fornecem evidências suficientes, no nível de 1% de significância, para concluir que a nota CEE e a APB não são independentes: a nota do exame de admissão tem poder preditivo.
Figure 11.4 Nota 11.9 “Exemplo 1”
Key Takeaways
- Valores críticos de uma distribuição qui-quadrado com graus de liberdade df são encontrados na Figura 12.4 “Valores críticos da distribuição qui-quadrado”.
- Um teste de qui-quadradoA teste baseado em uma estatística qui-quadrado para verificar se dois fatores são independentes. pode ser usado para avaliar a hipótese de que duas variáveis ou fatores aleatórios são independentes.
Exercícios
-
Pesquisa χ0.012 para cada um dos seguintes números de graus de liberdade.
- df=5
- df=11
- df=25
-
Localizar χ0.052 para cada um dos seguintes números de graus de liberdade.
- df=6
- df=12
- df=30
-
Find χ0.102 para cada um dos seguintes números de graus de liberdade.
- df=6
- df=12
- df=30
-
Find χ0.012 para cada um dos seguintes números de graus de liberdade.
- df=7
- df=10
- df=20
-
Para df=7 e α=0.05, find
- χα2
- χα22
-
Para df=17 e α=0.01, find
- χα2
- χα22
-
Uma amostra de dados é classificada em uma tabela de contingência de 2 × 2, baseada em dois fatores, cada um dos quais com dois níveis.
Factor 1 Level 1 Nível 2 Total de linha Factor 2 Nível 1 20 10 R Nível 2 15 5 R Total da coluna C C n - Encontre os totais da coluna, os totais das filas, e o total geral, n, da mesa.
- Encontrar o número E esperado de observações para cada célula com base na suposição de que os dois fatores são independentes (ou seja, basta usar a fórmula E=(R×C)∕n).
- Encontrar o valor da estatística do teste do qui-quadrado χ2.
- Ponte o número de graus de liberdade da estatística do teste de qui-quadrado.
-
Uma amostra de dados é classificada em uma tabela de contingência 3 × 2 com base em dois fatores, um dos quais com três níveis e o outro com dois níveis.
Factor 1 Nível 1 Nível 2 Total de linha Factor 2 Nível 1 20 10 R Nível 2 15 5 R Nível 3 10 20 R Total da coluna C C n - Encontrar os totais da coluna, os totais das filas, e o total geral, n, da mesa.
- Encontrar o número E esperado de observações para cada célula com base na suposição de que os dois fatores são independentes (ou seja, basta usar a fórmula E=(R×C)∕n).
- Encontrar o valor da estatística do teste do qui-quadrado χ2.
- Ponha o número de graus de liberdade da estatística do teste de qui-quadrado.
>
Basic
-
Um psicólogo infantil acredita que as crianças têm melhor desempenho nos testes quando lhes é dada liberdade de escolha percebida. Para testar essa crença, o psicólogo realizou um experimento no qual 200 alunos do terceiro ano foram designados aleatoriamente para dois grupos, A e B. A cada criança foi dado o mesmo teste lógico simples. Entretanto, no grupo B, cada criança recebeu a liberdade de escolher um livreto de texto entre muitos, com vários desenhos nas capas. O desempenho de cada criança foi classificado como Muito Bom, Bom, e Justo. Os resultados estão resumidos na tabela fornecida. Teste, ao nível de 5% de significância, se há evidências suficientes nos dados para apoiar a crença do psicólogo.
Grupo A B Desempenho Muito Bom 32 29 Bom 55 61 Fair 10 13 -
Em relação a concursos de prova de vinhos, Muitos especialistas afirmam que o primeiro copo de vinho servido estabelece um sabor de referência e que um vinho de referência diferente pode alterar a classificação relativa dos outros vinhos em competição. Para testar esta alegação, três vinhos, A, B e C, foram servidos num evento de prova de vinhos. A cada pessoa foi servido um único copo de cada vinho, mas em encomendas diferentes para convidados diferentes. No final, foi pedido a cada pessoa que nomeasse o melhor dos três. Cento e setenta e duas pessoas estavam no evento e as suas melhores colheitas são dadas na mesa fornecida. Teste, ao nível de 1% de significância, se existem provas suficientes nos dados para apoiar a alegação de que a preferência dos peritos em vinho depende do primeiro vinho servido.
Top Pick A B C Primeiro Vidro A 12 31 27 B 15 40 21 C 10 9 7 -
Será deixado…hereditárias? Para responder a esta pergunta, 250 adultos são seleccionados aleatoriamente e a sua mão e a mão dos seus pais são anotadas. Os resultados estão resumidos na tabela fornecida. Teste, ao nível de 1% de significância, se existem evidências suficientes nos dados para concluir que existe um elemento hereditário na mão.
Número de Pais Esquerdos.Entregue >0 1 2 Punho Esquerda 8 10 12 Direita 178 21 21 -
Alguns geneticistas afirmam que os genes que determinam a esquerda…A mão também governa o desenvolvimento dos centros de linguagem do cérebro. Se esta afirmação for verdadeira, então seria razoável esperar que as pessoas canhotas tendam a ter capacidades linguísticas mais fortes. Um estudo concebido para escrever esta afirmação seleccionou aleatoriamente 807 alunos que fizeram o Graduate Record Examination (GRE). As suas notas na parte linguística do exame foram classificadas em três categorias: baixa, média e alta, e a sua mão também foi notada. Os resultados são apresentados na tabela fornecida. Teste, ao nível de 5% de significância, se há evidência suficiente nos dados para concluir que as pessoas canhotas tendem a ter habilidades linguísticas mais fortes.
Pontuações em inglês Baixo Média Alto Pega de mão Esquerda 18 40 22 Direito 201 360 166 -
Acredita-se geralmente que as crianças educadas em famílias estáveis tendem a se sair bem na escola. Para verificar tal crença, um cientista social examinou 290 registros de alunos selecionados aleatoriamente em uma escola secundária pública e notou a estrutura familiar e o status acadêmico de cada aluno quatro anos após entrar na escola secundária. Os dados foram então classificados em uma tabela de contingência de 2 × 3 com dois fatores. O fator 1 tem dois níveis: graduado e não graduado. O fator 2 tem três níveis: nenhum dos pais, um dos pais e dois pais. Os resultados são apresentados na tabela fornecida. Teste, ao nível de 1% de significância, se há evidência suficiente nos dados para concluir que a estrutura familiar é importante no desempenho escolar dos alunos.
Situação acadêmica Graduado Não Graduado Família Sem pais 18 31 Um dos pais 101 44 Dois pais 70 26 -
Um administrador de uma grande escola média deseja usar a influência das celebridades para encorajar os alunos a fazer escolhas mais saudáveis no refeitório da escola. A cafeteria está situada no centro de um espaço aberto. Todos os dias, na hora do almoço, os alunos almoçam e bebem uma bebida em três linhas separadas que levam a três estações de serviço separadas. Como experiência, o administrador da escola exibiu um cartaz de uma popular estrela pop adolescente bebendo leite em cada uma das três áreas onde as bebidas são fornecidas, exceto que o leite no cartaz é diferente em cada local: um mostra leite branco, outro mostra leite rosa com sabor de morango e outro mostra leite com chocolate. Após o primeiro dia da experiência, o administrador anotou as escolhas de leite dos alunos separadamente para as três linhas. Os dados são apresentados na tabela fornecida. Teste, ao nível de 1% de significância, se há evidência suficiente nos dados para concluir que os cartazes tiveram algum impacto nas escolhas de bebida dos alunos.
Student Choice Regular Strawberry Chocolate Poster Choice Regular 38 28 40 Strawberry 18 51 24 Chocolate 32 32 53
Aplicações
-
Large Data Set 8 registra o resultado de uma pesquisa com 300 adultos selecionados aleatoriamente que vão ao cinema regularmente. Para cada pessoa foi registrado o sexo e o tipo de filme preferido. Teste, ao nível de 5% de significância, se há evidência suficiente nos dados para concluir que os fatores “sexo” e “tipo preferido de filme” são dependentes.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Grande Data Set Exercise
Respostas
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0,6698, χ0.052=5.99, não rejeitar H0
-
χ2=72.35, χ0.012=9.21, rejeitar H0
-
χ2=21.2784, χ0.012=9.21, rejeite H0
-
χ2=28.4539. df=3. Região de Rejeição: [7.815,∞). Decisão: Rejeitar H0 da independência.