Pruebas de independencia
Las pruebas de hipótesis encontradas anteriormente en el libro tenían que ver con la comparación de los valores numéricos de dos parámetros de la población. En esta subsección investigaremos hipótesis que tienen que ver con si dos variables aleatorias toman o no sus valores de forma independiente, o si el valor de una tiene relación con el valor de la otra. Por tanto, las hipótesis se expresarán con palabras, no con símbolos matemáticos. Construimos la discusión en torno al siguiente ejemplo.
Existe la teoría de que el sexo de un bebé en el vientre materno está relacionado con su frecuencia cardíaca: las niñas tienden a tener una mayor frecuencia cardíaca. Supongamos que queremos comprobar esta teoría. Examinamos los registros de frecuencia cardíaca de 40 bebés tomados durante los últimos controles prenatales de sus madres antes del parto, y a cada uno de estos 40 registros seleccionados al azar le calculamos los valores de dos medidas aleatorias: 1) el sexo y 2) la frecuencia cardíaca. En este contexto, estas dos medidas aleatorias suelen denominarse factoresUna variable con varios niveles cualitativos.. Dado que la carga de la prueba es que la frecuencia cardíaca y el género están relacionados, no que no estén relacionados, el problema de probar la teoría sobre el género del bebé y la frecuencia cardíaca puede formularse como una prueba de las siguientes hipótesis:
H0:El género del bebé y la frecuencia cardíaca del bebé son independientesvs. Ha:El género del bebé y la frecuencia cardíaca del bebé no son independientes
El factor género tiene dos categorías o niveles naturales: niño y niña. Dividimos el segundo factor, la frecuencia cardíaca, en dos niveles, bajo y alto, eligiendo una frecuencia cardíaca, por ejemplo 145 latidos por minuto, como límite entre ambos. Una frecuencia cardíaca inferior a 145 pulsaciones por minuto se considerará baja y 145 y más, alta. Los 40 registros dan lugar a una tabla de contingencia de 2 × 2. Uniendo los totales de las filas, los totales de las columnas y un total general obtenemos la tabla que se muestra como Tabla 11.1 «Sexo del bebé y frecuencia cardíaca». Las cuatro entradas en negrita son recuentos de observaciones de la muestra de n = 40. Había 11 niñas con frecuencia cardíaca baja, 17 niños con frecuencia cardíaca baja, y así sucesivamente. Forman el núcleo de la tabla ampliada.
Tabla 11.1 Género del bebé y frecuencia cardíaca
| Ritmo cardíaco | ||||
|---|---|---|---|---|
| Bajo | Alto | Total de filas | ||
| Género | Niña | 11 | 7 | 18 |
| Chico | 17 | 5 | 22 | |
| Total de la columna | 28 | 12 | Total = 40 | |
En analogía con el hecho de que la probabilidad de eventos independientes es el producto de las probabilidades de cada evento, si la frecuencia cardíaca y el sexo fueran independientes, entonces esperaríamos que el número de cada celda del núcleo fuera cercano al producto del total de la fila R y el total de la columna C de la fila y la columna que la contienen, dividido por el tamaño de la muestra n. Denotando tal número esperado de observaciones E, estos cuatro valores esperados son:
- 1ª fila y 1ª columna: E=(R×C)∕n=18×28∕40=12,6
- 1ª fila y 2ª columna: E=(R×C)∕n=18×12∕40=5,4
- Segunda fila y 1ª columna: E=(R×C)∕n=22×28∕40=15,4
- Segunda fila y 2ª columna: E=(R×C)∕n=22×12∕40=6,6
Actualizamos la tabla 11.1 «Sexo del bebé y frecuencia cardíaca» colocando cada valor esperado en su celda central correspondiente, justo debajo del valor observado en la celda. Esto da la tabla actualizada Tabla 11.2 «Sexo del bebé y frecuencia cardíaca actualizados».
Tabla 11.2 Género del bebé y frecuencia cardíaca actualizados
| Ritmo cardíaco | ||||
|---|---|---|---|---|
| Bajo | Alta | Total de filas | ||
| Género | Chica | O=11E=12.6 | O=7E=5,4 | R = 18 |
| Chico | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Total de la columna | C = 28 | C = 12 | n = 40 | |
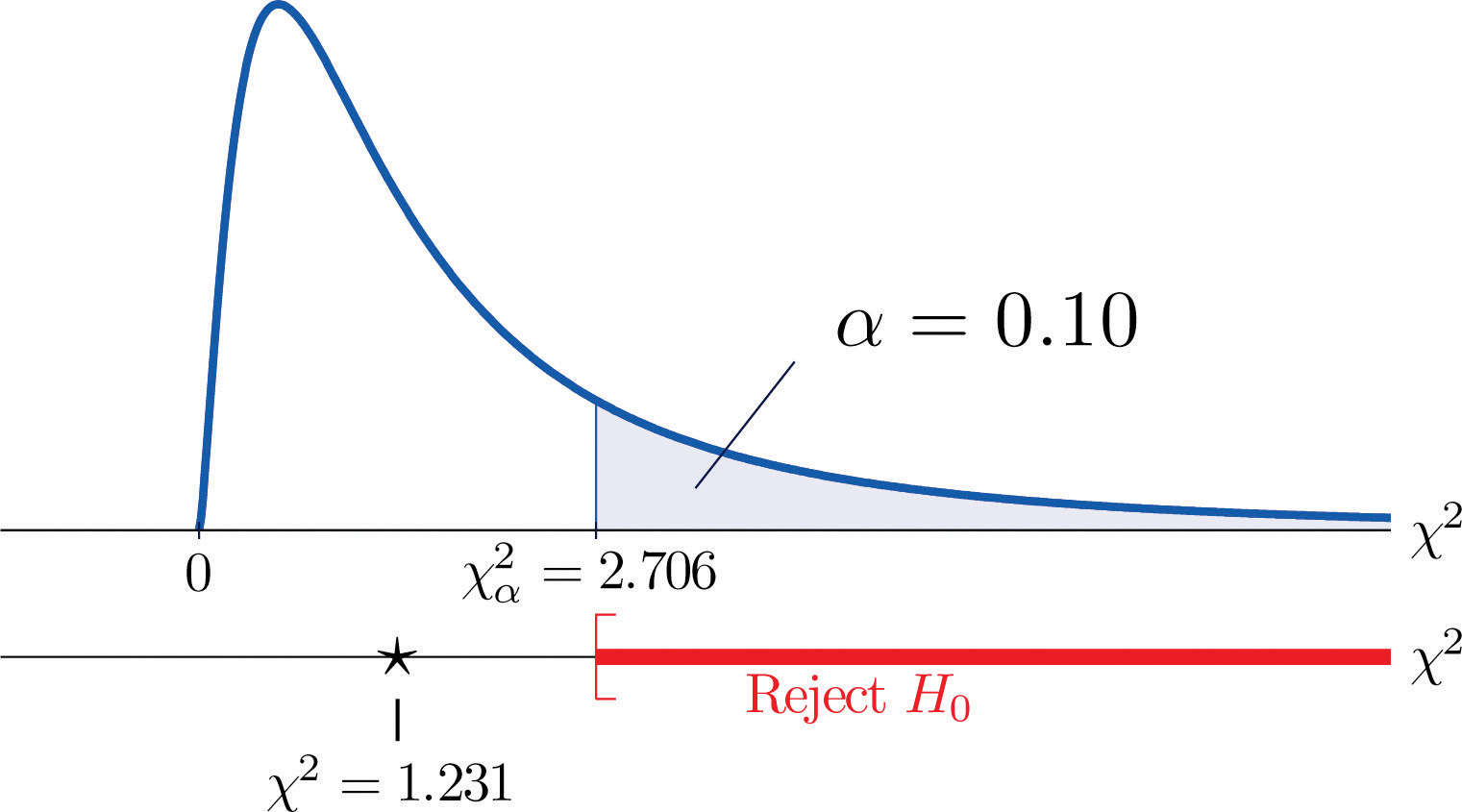
Una medida de cuánto se desvían los datos de lo que esperaríamos ver si los factores fueran realmente independientes es la suma de los cuadrados de la diferencia de los números en cada celda del núcleo, o, estandarizando dividiendo cada cuadrado por el número esperado en la celda, la suma Σ(O-E)2∕E. Rechazaríamos la hipótesis nula de que los factores son independientes sólo si este número es grande, por lo que la prueba es de cola derecha. En este ejemplo, la variable aleatoria Σ(O-E)2∕E tiene la distribución chi-cuadrado con un grado de libertad. Si hubiéramos decidido al principio hacer la prueba al nivel de significación del 10%, el valor crítico que define la región de rechazo sería, leyendo la figura 12.4 «Valores críticos de las distribuciones chi-cuadrado», χα2=χ0,102=2,706, de modo que la región de rechazo sería el intervalo [2,706,∞). Al calcular el valor del estadístico estandarizado de la prueba obtenemos
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Como 1,231 < 2,706, la decisión es no rechazar H0. Véase la Figura 11.3 «Predicción del sexo del bebé». Los datos no proporcionan suficiente evidencia, al nivel de significación del 10%, para concluir que la frecuencia cardíaca y el género están relacionados.
Figura 11.3 Predicción del género del bebé
Con este ejemplo específico en mente, pase ahora a la situación general. En la situación general de probar la independencia de dos factores, llámelos Factor 1 y Factor 2, las hipótesis a probar son
H0:Los dos factores son independientesvs. Ha:Los dos factores no son independientes
Como en el ejemplo, cada factor se divide en un número de categorías o niveles. Éstos pueden surgir de forma natural, como en la división del género entre niños y niñas, o de forma algo arbitraria, como en la división de la frecuencia cardíaca entre alta y baja. Supongamos que el Factor 1 tiene niveles I y el Factor 2 tiene niveles J. Entonces la información de una muestra aleatoria da lugar a una tabla de contingencia general I × J, que con los totales de las filas, los totales de las columnas y un total general aparecería como se muestra en la Tabla 11.3 «Tabla de contingencia general». Cada celda puede ser etiquetada por un par de índices (i,j). Oij representa el recuento observado de observaciones en la celda en la fila i y la columna j, Ri el total de la fila i y Cj el total de la columna j. Para simplificar la notación, eliminaremos los índices, por lo que la Tabla 11.3 «Tabla de contingencia general» se convierte en la Tabla 11.4 «Tabla de contingencia general simplificada». Sin embargo, es importante tener en cuenta que los Os, los Rs y los Cs, aunque se denotan con los mismos símbolos, son en realidad números diferentes.
Tabla 11.3 Tabla general de contingencias
| Niveles del factor 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Total de filas | ||
| Niveles del factor 1 | 1 | O11 | – – | O1j | – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – | Oij | – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OI1 | – – – | OIj | – – | OIJ | RI | |
| Total de la columna | C1 | – – – | Cj | – – | CJ | n | |
Tabla 11.4 Tabla de contingencia general simplificada
| Niveles del factor 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Total de filas | ||
| Niveles del factor 1 | 1 | O | – – | O | – – | O | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| i | O | – – | O | – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | O | – – – | O | – – | O | R | |
| Total de la columna | C | – – – | C | – – | C | n | |
Como en el ejemplo, para cada celda central de la tabla calculamos cuál sería el número esperado E de observaciones si los dos factores fueran independientes. E se calcula para cada celda central (cada celda con una O en ella) de la tabla 11.4 «Tabla de contingencia general simplificada» mediante la regla aplicada en el ejemplo:
donde R es el total de filas y C es el total de columnas correspondiente a la celda, y n es el tamaño de la muestra.
Después de calcular el número esperado para cada celda, la Tabla 11.4 «Tabla de Contingencia General Simplificada» se actualiza para formar la Tabla 11.5 «Tabla de Contingencia General Actualizada» insertando el valor calculado de E en cada celda del núcleo.
Tabla 11.5 Tabla de contingencia general actualizada
| Niveles del factor 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Total de filas | ||
| Niveles del factor 1 | 1 | OE | – – | OE | – – | OE | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | OE | – – – | OE | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – | OE | – – – | OE | R | |
| Total de la columna | C | – – | C | – – | C | n | |
Aquí está la estadística de prueba para la hipótesis general basada en la Tabla 11.5 «Tabla de Contingencia General Actualizada», junto con las condiciones de que siga una distribución chi-cuadrado.
Estadística de prueba para probar la independencia de dos factores
χ2=Σ(O-E)2E
donde la suma es sobre todas las celdas centrales de la tabla.
Si
- los dos factores de estudio son independientes, y
- el recuento observado O de cada celda de la tabla 11.5 «Tabla de contingencia general actualizada» es al menos 5,
entonces χ2 sigue aproximadamente una distribución chi-cuadrado con df=(I-1)×(J-1) grados de libertad.
Se utilizan los mismos procedimientos de cinco pasos, ya sea el enfoque del valor crítico o el enfoque del valor p, que se introdujeron en la sección 8.1 «Los elementos de la prueba de hipótesis» y en la sección 8.3 «La significación observada de una prueba» del capítulo 8 «Prueba de hipótesis» para realizar la prueba, que siempre es de cola derecha.
Ejemplo 1
Un investigador desea investigar si las puntuaciones de los estudiantes en un examen de acceso a la universidad (CEE) tienen algún poder indicativo del futuro rendimiento universitario medido por el GPA. En otras palabras, desea investigar si los factores CEE y GPA son independientes o no. Selecciona aleatoriamente a n = 100 estudiantes de una universidad y anota la puntuación de cada estudiante en el examen de ingreso y su media de notas al final del segundo año. Divide las puntuaciones de la prueba de acceso en dos niveles y las medias de notas en tres niveles. Ordenando los datos según estas divisiones, forma la tabla de contingencia que se muestra en la Tabla 11.6 «Tabla de contingencia CEE versus GPA», en la que ya se han calculado los totales de las filas y columnas.
Tabla 11.6 Tabla de contingencia CEE versus GPA
| GPA | |||||
|---|---|---|---|---|---|
| 2,7 | 2,7 a 3,2 | >3.2 | Total de filas | ||
| CEE | 1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Total de la columna | 41 | 36 | 23 | Total=100 | |
Test, al nivel de significación del 1%, si estos datos proporcionan pruebas suficientes para concluir que las puntuaciones del CEE indican los futuros niveles de rendimiento de los estudiantes universitarios de primer año, medidos por el GPA.
Solución:
Realizamos la prueba utilizando el enfoque del valor crítico, siguiendo el método habitual de cinco pasos descrito al final de la sección 8.1 «Los elementos de la prueba de hipótesis» en el capítulo 8 «Prueba de hipótesis».
-
Paso 1. Las hipótesis son
H0:CEE y GPA son factores independientesvs. Ha:CEE y GPA no son factores independientes
- Paso 2. La distribución es chi-cuadrado.
-
Paso 3. Para calcular el valor del estadístico de la prueba debemos calcular primero el número esperado para cada una de las seis celdas del núcleo (las que tienen entradas en negrita):
- 1ª fila y 1ª columna: E=(R×C)∕n=41×52∕100=21,32
- 1ª fila y 2ª columna: E=(R×C)∕n=36×52∕100=18,72
- 1ª fila y 3ª columna: E=(R×C)∕n=23×52∕100=11,96
- Segunda fila y 1ª columna: E=(R×C)∕n=41×48∕100=19,68
- Segunda fila y 2ª columna: E=(R×C)∕n=36×48∕100=17,28
- Segunda fila y 3ª columna: E=(R×C)∕n=23×48∕100=11,04
La Tabla 11.6 «Tabla de Contingencia CEE versus GPA» se actualiza a la Tabla 11.7 «Tabla de Contingencia CEE versus GPA actualizada».
Tabla 11.7 Tabla de contingencia actualizada de CEE versus GPA
GPA <2,7 2.7 a 3,2 >3,2 Total de filas CEE 1800 O=35E=21.32 O=12E=18,72 O=5E=11,96 R = 52 ≥1800 O=6E=19,68 O=24E=17,28 O=18E=11.04 R = 48 Total de la columna C = 41 C = 36 C = 23 n = 100 La estadística de la prueba es
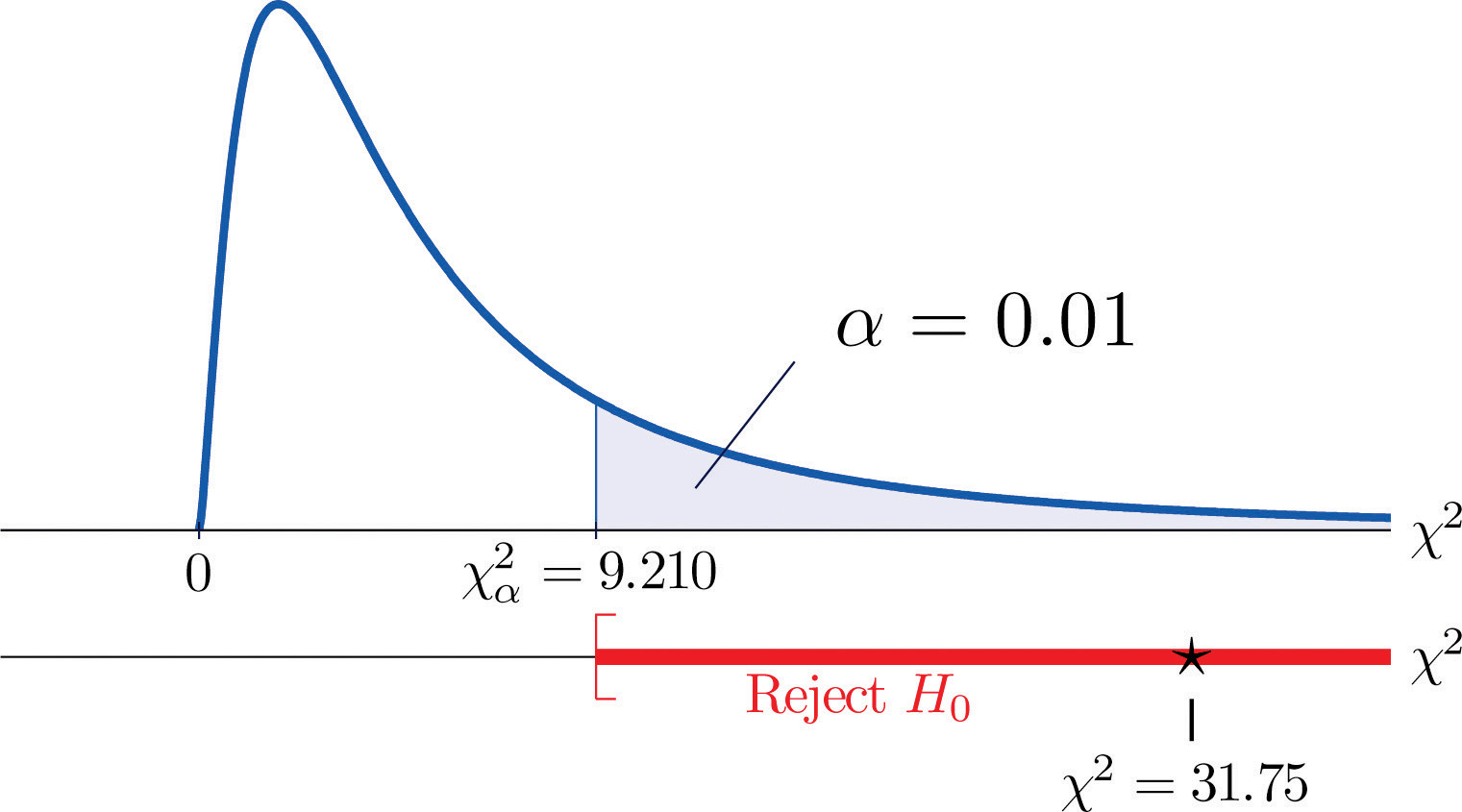
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Como el factor CEE tiene dos niveles y el factor GPA tiene tres, I = 2 y J = 3. Por tanto, la estadística de la prueba sigue la distribución chi-cuadrado con df=(2-1)×(3-1)=2 grados de libertad.
Como la prueba es de cola derecha, el valor crítico es χ0,012. Leyendo la figura 12.4 «Valores críticos de las distribuciones chi-cuadrado», χ0,012=9,210, por lo que la región de rechazo es [9,210,∞).
- Paso 5. Como 31,75 > 9,21 la decisión es rechazar la hipótesis nula. Véase la figura 11.4. Los datos proporcionan evidencia suficiente, al nivel de significación del 1%, para concluir que la puntuación del CEE y el GPA no son independientes: la puntuación del examen de ingreso tiene poder predictivo.
Figura 11.4 Nota 11.9 «Ejemplo 1»
Valores críticos de una distribución chi-cuadrado con grados de libertad df se encuentran en la Figura 12.4 «Valores críticos de las distribuciones chi-cuadrado».
Ejercicios
-
Busque χ0,012 para cada uno de los siguientes números de grados de libertad.
- df=5
- df=11
- df=25
-
Encuentra χ0,052 para cada uno de los siguientes números de grados de libertad.
- df=6
- df=12
- df=30
-
Encuentra χ0.102 para cada uno de los siguientes números de grados de libertad.
- df=6
- df=12
- df=30
-
Encuentra χ0.012 para cada uno de los siguientes números de grados de libertad.
- df=7
- df=10
- df=20
-
Para df=7 y α=0.05, hallar
- χα2
- χα22
-
Para df=17 y α=0.01, halle
- χα2
- χα22
-
Una muestra de datos se ordena en una tabla de contingencia 2 × 2 basada en dos factores, cada uno de los cuales tiene dos niveles.
Factor 1 Nivel 1 Nivel 2 Total de filas Factor 2 Nivel 1 20 10 R Nivel 2 15 5 R Total de columna C C n - Encuentra los totales de columna, los totales de las filas y el total general, n, de la tabla.
- Hallar el número esperado E de observaciones para cada celda basándose en la suposición de que los dos factores son independientes (es decir, sólo hay que utilizar la fórmula E=(R×C)∕n).
- Hallar el valor del estadístico de la prueba de chi-cuadrado χ2.
- Hallar el número de grados de libertad del estadístico de la prueba chi-cuadrado.
-
Una muestra de datos se ordena en una tabla de contingencia de 3 × 2 basada en dos factores, uno de los cuales tiene tres niveles y el otro tiene dos niveles.
Factor 1 Nivel 1 Nivel 2 Total de filas Factor 2 Nivel 1 20 10 R Nivel 2 15 5 R Nivel 3 10 20 R Total de columna C C n - Encuentra los totales de columna, los totales de las filas y el total general, n, de la tabla.
- Hallar el número esperado E de observaciones para cada celda basándose en la suposición de que los dos factores son independientes (es decir, sólo hay que utilizar la fórmula E=(R×C)∕n).
- Hallar el valor del estadístico de la prueba de chi-cuadrado χ2.
- Encuentre el número de grados de libertad del estadístico de la prueba chi-cuadrado.
Básico
-
Un psicólogo infantil cree que los niños rinden mejor en los exámenes cuando se les da una libertad de elección percibida. Para comprobar esta creencia, el psicólogo llevó a cabo un experimento en el que 200 niños de tercer grado fueron asignados al azar a dos grupos, A y B. A cada niño se le hizo la misma prueba de lógica simple. Sin embargo, en el grupo B, se dio a cada niño la libertad de elegir un folleto de texto entre muchos con diversos dibujos en las cubiertas. El rendimiento de cada niño se calificó como Muy bueno, Bueno y Regular. Los resultados se resumen en la tabla que se presenta. Pruebe, al nivel de significación del 5%, si hay suficiente evidencia en los datos para apoyar la creencia del psicólogo.
Grupo A B Rendimiento Muy Bueno 32 29 Buena 55 61 Justa 10 13 -
En cuanto a los concursos de cata de vinos, muchos expertos afirman que la primera copa de vino servida establece un sabor de referencia y que un vino de referencia diferente puede alterar la clasificación relativa de los demás vinos en competición. Para comprobar esta afirmación, se sirvieron tres vinos, A, B y C, en una cata de vinos. A cada persona se le sirvió una sola copa de cada vino, pero en diferentes órdenes para diferentes invitados. Al final, se pidió a cada persona que nombrara el mejor de los tres. Ciento setenta y dos personas asistieron al evento y sus mejores elecciones se recogen en la tabla proporcionada. Pruebe, al nivel de significación del 1%, si hay suficiente evidencia en los datos para apoyar la afirmación de que la preferencia de los expertos en vino depende del primer vino servido.
Elección superior A B C Primera copa A 12 31 27 B 15 40 21 C 10 9 7 -
¿Ser zurdohereditario? Para responder a esta pregunta, se seleccionan al azar 250 adultos y se anota su lateralidad y la de sus padres. Los resultados se resumen en la tabla que se presenta. Compruebe, con un nivel de significación del 1%, si hay pruebas suficientes en los datos para concluir que existe un elemento hereditario en la lateralidad.
Número de padres zurdosHanded 0 1 2 Handedness Left 8 10 12 Derecha 178 21 21 -
Algunos genetistas afirman que los genes que determinan la zurderazurdos también gobiernan el desarrollo de los centros del lenguaje del cerebro. Si esta afirmación es cierta, sería razonable esperar que los zurdos tiendan a tener mayores capacidades lingüísticas. En un estudio diseñado para comprobar esta afirmación se seleccionaron al azar 807 estudiantes que se presentaron al Graduate Record Examination (GRE). Sus puntuaciones en la parte lingüística del examen se clasificaron en tres categorías: baja, media y alta, y también se anotó su lateralidad. Los resultados se recogen en la tabla adjunta. Compruebe, con un nivel de significación del 5%, si hay pruebas suficientes en los datos para concluir que los zurdos tienden a tener mayores capacidades lingüísticas.
Puntajes de inglés del GRE Bajo Promedio Alta Derecha Izquierda 18 40 22 Derecha 201 360 166 -
Se cree generalmente que los niños criados en familias estables tienden a tener un buen rendimiento escolar. Para verificar tal creencia, un científico social examinó los expedientes de 290 estudiantes seleccionados al azar en un instituto público y anotó la estructura familiar y la situación académica de cada uno de ellos cuatro años después de entrar en el instituto. A continuación, los datos se ordenaron en una tabla de contingencia de 2 × 3 con dos factores. El factor 1 tiene dos niveles: graduado y no graduado. El factor 2 tiene tres niveles: ningún padre, un padre y dos padres. Los resultados se recogen en la tabla proporcionada. Pruebe, al nivel de significación del 1%, si hay suficiente evidencia en los datos para concluir que la estructura familiar importa en el rendimiento escolar de los estudiantes.
Estado académico Se graduó No se graduó Familia Sin padres 18 31 Un padre 101 44 Dos padres 70 26 -
El administrador de un gran centro de enseñanza media desea utilizar la influencia de los famosos para animar a los alumnos a tomar decisiones más saludables en la cafetería del centro. La cafetería está situada en el centro de un espacio abierto. Todos los días, a la hora del almuerzo, los estudiantes reciben su comida y una bebida en tres filas separadas que conducen a tres estaciones de servicio separadas. A modo de experimento, el administrador del centro escolar expuso un póster de una popular estrella del pop adolescente bebiendo leche en cada una de las tres zonas en las que se sirven las bebidas, con la salvedad de que la leche del póster es diferente en cada lugar: en uno aparece la leche blanca, en otro la leche rosa con sabor a fresa y en otro la leche de chocolate. Tras el primer día del experimento, el administrador anotó las elecciones de leche de los alumnos por separado en las tres líneas. Los datos se recogen en la tabla proporcionada. Pruebe, al nivel de significación del 1%, si hay suficiente evidencia en los datos para concluir que los carteles tuvieron algún impacto en las elecciones de bebidas de los estudiantes.
Elección del estudiante Regular Fresa Chocolate Elección del cartel Regular 38 28 40 Fresa 18 51 24 Chocolate 32 32 53
Aplicaciones
-
Grande El conjunto de datos 8 registra el resultado de una encuesta realizada a 300 adultos seleccionados al azar que van a las salas de cine con regularidad. Para cada persona se registró el género y el tipo de película preferido. Pruebe, con un nivel de significación del 5%, si hay suficiente evidencia en los datos para concluir que los factores «género» y «tipo de película preferido» son dependientes.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Grande Ejercicio de conjunto de datos
Respuestas
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0,6698, χ0.052=5,99, no rechaza H0
-
χ2=72,35, χ0,012=9,21, rechaza H0
-
χ2=21.2784, χ0.012=9.21, rechazar H0
-
χ2=28.4539. df=3. Región de rechazo: [7.815,∞). Decisión: Rechazar H0 de independencia.