Riippumattomuustestit
Kirjassa aiemmin kohdatut hypoteesitestit liittyivät siihen, miten kahden populaatioparametrin numeerisia arvoja verrataan toisiinsa. Tässä alaluvussa tutkimme hypoteeseja, jotka liittyvät siihen, ottavatko kaksi satunnaismuuttujaa arvonsa itsenäisesti vai onko toisen arvolla yhteys toisen arvoon. Hypoteesit ilmaistaan siis sanoin, ei matemaattisin symbolein. Rakennamme keskustelun seuraavan esimerkin ympärille.
On olemassa teoria, jonka mukaan kohdussa olevan vauvan sukupuoli on yhteydessä vauvan sykkeeseen: tyttövauvoilla on yleensä korkeampi syke. Oletetaan, että haluamme testata tätä teoriaa. Tutkimme 40 vauvan syketietoja, jotka on otettu äitiensä viimeisten synnytystä edeltävien raskaudenaikaisten tarkastusten aikana ennen synnytystä, ja jokaiselle näistä 40 satunnaisesti valitusta tietueesta laskemme kahden satunnaismitan arvot: 1) sukupuoli ja 2) syke. Tässä yhteydessä näitä kahta satunnaismittaa kutsutaan usein tekijöiksiMuuttuja, jolla on useita laadullisia tasoja… Koska todistustaakka on se, että syke ja sukupuoli ovat yhteydessä toisiinsa, ei se, että ne eivät ole yhteydessä toisiinsa, vauvan sukupuolta ja sykettä koskevan teorian testausongelma voidaan muotoilla seuraavien hypoteesien testaamiseksi:
H0:Vauvan sukupuoli ja vauvan syke ovat riippumattomiavs. Ha:Vauvan sukupuoli ja vauvan syke eivät ole riippumattomia
Tekijällä sukupuoli on kaksi luonnollista luokkaa tai tasoa: poika ja tyttö. Jaamme toisen tekijän, sykkeen, kahteen tasoon, matalaan ja korkeaan, valitsemalla niiden väliseksi raja-arvoksi jonkin sykkeen, esimerkiksi 145 lyöntiä minuutissa. Alle 145 lyöntiä minuutissa olevaa sykettä pidetään matalana ja yli 145 lyöntiä minuutissa olevaa sykettä korkeana. 40 tietueesta saadaan 2 × 2 kontingenssitaulukko. Yhdistämällä rivien summat, sarakkeiden summat ja kokonaissumma saadaan taulukko, joka esitetään taulukkona 11.1 ”Vauvan sukupuoli ja syke”. Neljä lihavoitua merkintää ovat havaintojen lukumäärät otoksesta n = 40. Tyttöjä, joilla oli alhainen syke, oli 11, poikia, joilla oli alhainen syke, oli 17 ja niin edelleen. Ne muodostavat laajennetun taulukon ytimen.
Taulukko 11.1 Vauvan sukupuoli ja syke
| Syke | ||||
|---|---|---|---|---|
| matala | korkea | Rivi yhteensä | ||
| Sukupuoli | Tyttö | 11 | 7 | 18 |
| Poika | 17 | 5 | 22 | |
| Sarake Yhteensä | 28 | 12 | Total = 40 | |
Analogisesti sen tosiasian kanssa, että riippumattomien tapahtumien todennäköisyys on kunkin tapahtuman todennäköisyyksien tulo, jos syke ja sukupuoli olisivat riippumattomia, odottaisimme kunkin ydinsolun lukumäärän olevan lähellä sen sisältävän rivin ja sarakkeen rivin ja sarakkeen kokonaissumman R ja sarakkeen kokonaissumman C tuloa jaettuna otoskoolla n. Merkitään tällaista odotettua havaintojen lukumäärää E, ja nämä neljä odotusarvoa ovat:
- 1. rivi ja 1. sarake: E=(R×C)∕n=18×28∕40=12.6
- 1. rivi ja 2. sarake: E=(R×C)∕n=18×12∕40=5.4
- 2. rivi ja 1. sarake: E=(R×C)∕n=22×28∕40=15.4
- 2. rivi ja 2. sarake: E=(R×C)∕n=22×12∕40=6.6
Päivitämme taulukkoa 11.1 ”Vauvan sukupuoli ja syketaajuus” sijoittamalla kunkin odotusarvon vastaavaan ydinsoluunsa, suoraan solun havaitun arvon alle. Näin saadaan päivitetty taulukko Taulukko 11.2 ”Päivitetty vauvan sukupuoli ja syke”.
Taulukko 11. Taulukko 11.2 ”Vauvan sukupuoli ja syke”.2 Päivitetty vauvan sukupuoli ja syke
| Syke | ||||
|---|---|---|---|---|
| Matalat | Korkea | Rivi yhteensä | ||
| Sukupuoli | Tyttö | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Poika | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Sarake Yhteensä | C = 28 | C = 12 | n = 40 | |
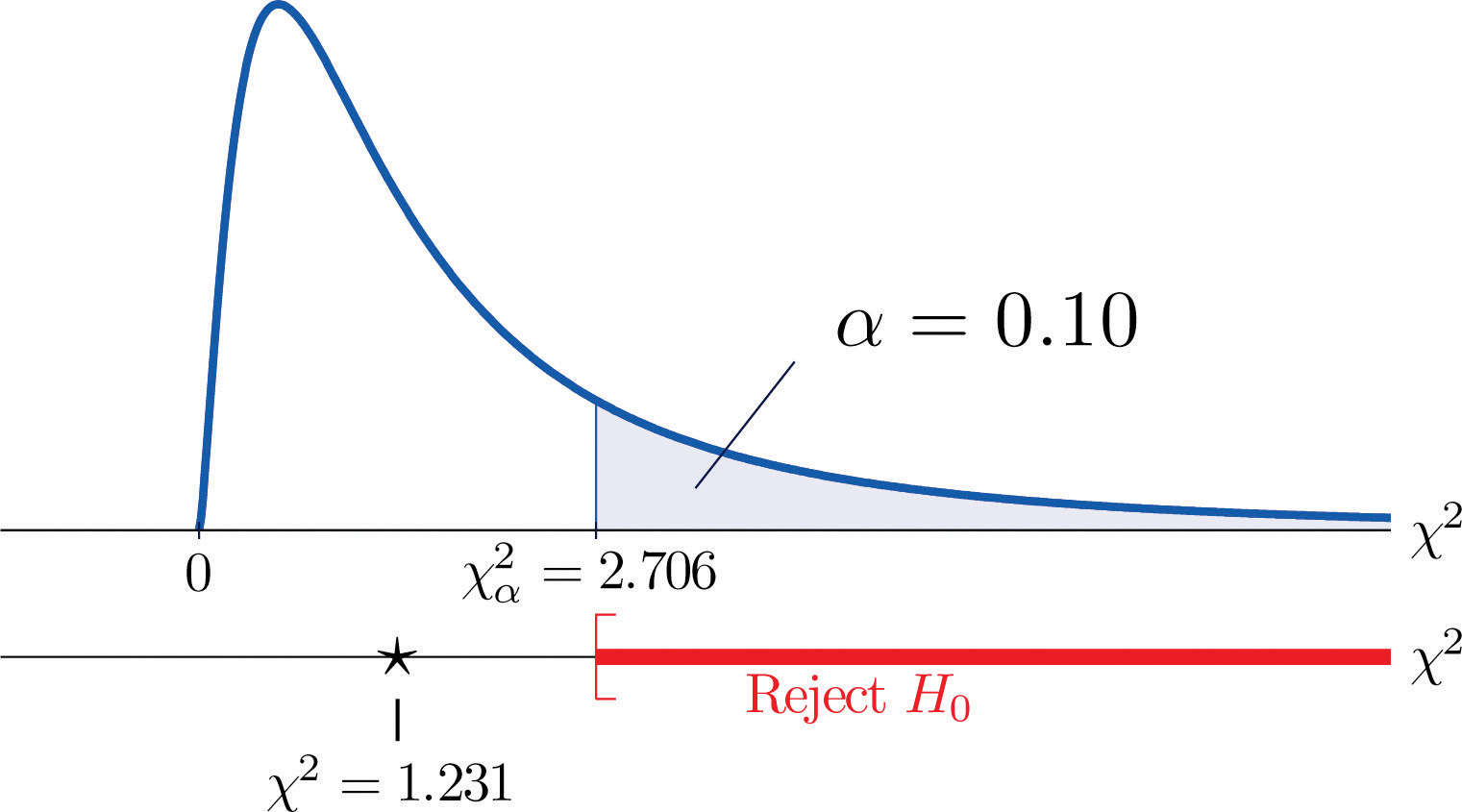
Mittari siitä, kuinka paljon aineisto poikkeaa siitä, mitä odottaisimme näkevämme, jos tekijät todella olisivat riippumattomia, on kussakin ytimessä olevien lukujen lukujen erotuksen neliöiden summa, tai, vakioimalla jakamalla kukin neliö solun odotetulla lukumäärällä, summa Σ(O-E)2∕E. Hylkäämme nollahypoteesin, jonka mukaan tekijät ovat riippumattomia, vain jos tämä luku on suuri, joten testi on oikeanpuoleinen. Tässä esimerkissä satunnaismuuttujalla Σ(O-E)2∕E on chi-neliöjakauma yhdellä vapausasteella. Jos olisimme aluksi päättäneet testata 10 prosentin merkitsevyystasolla, hylkäysalueen määrittelevä kriittinen arvo olisi kuvasta 12.4 ”Chi-neliöjakaumien kriittiset arvot” luettuna χα2=χ0,102=2,706, joten hylkäysalue olisi väli [2,706,∞). Kun lasketaan standardoidun testistatistiikan arvo, saadaan
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Koska 1,231 < 2,706, päätetään, ettei H0 hylätä. Katso kuva 11.3 ”Vauvan sukupuolen ennustaminen”. Aineisto ei anna riittävää näyttöä 10 %:n merkitsevyystasolla päätellä, että syke ja sukupuoli ovat yhteydessä toisiinsa.
Kuvio 11.3 Vauvan sukupuolen ennustaminen
Tämän konkreettisen esimerkin jälkeen siirrytään nyt yleiseen tilanteeseen. Yleisessä tilanteessa, jossa testataan kahden tekijän riippumattomuutta, sanotaan niitä tekijäksi 1 ja tekijäksi 2, testattavat hypoteesit ovat
H0:Kaksi tekijää ovat riippumattomiavs. Ha:Kaksi faktoria eivät ole riippumattomia
Esimerkissä kukin faktori on jaettu useisiin luokkiin tai tasoihin. Nämä voivat syntyä luonnollisesti, kuten sukupuolen poika-tyttö -jaottelussa, tai jokseenkin mielivaltaisesti, kuten sykkeen korkea-matala -jaottelussa. Oletetaan, että tekijällä 1 on I-tasot ja tekijällä 2 J-tasot. Tällöin satunnaisotoksesta saaduista tiedoista saadaan yleinen I × J -kontingenssitaulukko, joka rivien, sarakkeiden ja kokonaissumman summineen näyttäisi taulukossa 11.3 ”Yleinen kontingenssitaulukko” esitetyllä tavalla. Jokainen solu voidaan merkitä indeksiparilla (i,j). Oij tarkoittaa solussa rivillä i ja sarakkeessa j olevien havaintojen havaittua lukumäärää, Ri tarkoittaa i:nnen rivin kokonaissummaa ja Cj j:nnen sarakkeen kokonaissummaa. Merkintätavan yksinkertaistamiseksi jätämme indeksit pois, joten taulukko 11.3 ”Yleinen satunnaisvaihtelutaulukko” muuttuu taulukoksi 11.4 ”Yksinkertaistettu yleinen satunnaisvaihtelutaulukko”. On kuitenkin tärkeää pitää mielessä, että vaikka Os:t, R:t ja Cs:t merkitään samoilla symboleilla, ne ovat itse asiassa eri lukuja.
Taulukko 11.3 Yleinen kontingenssitaulukko
| Tekijä 2 tasot | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Rivi yhteensä | |||
| Tekijä 1 Tasot | 1 | O11 | – – – | O1j | – – – – | O1J | R1 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| i | Oi1 | – – – | Oij | – – – | OiJ | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| I | OI1 | – – – | OIj | – – – | OIJ | RI | ||
| Sarake Yhteensä | C1 | – – – – | Cj | – – – – | CJ | n | ||
Taulukko 11.4 Yksinkertaistettu yleinen varmuustaulukko
| Tekijän 2 tasot | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Rivi yhteensä | |||||||||||||||||||||
| Tekijä 1 Tasot | 1 | O | – – – | O | – – – | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O | O |
| i | O | – – – | O | – – – | O | R | ||||||||||||||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||||||||||||||||||
| I | O | – – – | O | – – – | O | R | ||||||||||||||||||||
| Sarake yhteensä | C | C | – – – | C | – – – | C | n | |||||||||||||||||||
Kuten esim, jokaiselle taulukon ydinsolulle lasketaan, mikä olisi havaintojen odotettu määrä E, jos kaksi tekijää olisivat riippumattomia. E lasketaan kullekin taulukon 11.4 ”Yksinkertaistettu yleinen kontingenssitaulukko” ydinsolulle (jokainen solu, jossa on O) esimerkissä sovelletulla säännöllä:
missä R on solua vastaava rivien kokonaismäärä ja C on sarakkeiden kokonaismäärä ja n on otoskoko.
Kun odotettu luku on laskettu jokaiselle solulle, taulukko 11.4 ”Yksinkertaistettu yleinen sattumanvaraisuustaulukko” päivitetään taulukoksi 11.5 ”Päivitetty yleinen sattumanvaraisuustaulukko” lisäämällä laskettu E:n arvo kuhunkin ydinsoluun.
Taulukko 11. Taulukko 11.4 ”Päivitetty yleinen sattumanvaraisuustaulukko”.5 Päivitetty yleinen ennakoimattomuustaulukko
| Tekijän 2 tasot | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Rivi yhteensä | ||||
| Tekijä 1 Tasot | 1 | OE | – – – | OE | – – – | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | OE | – – – | OE | – – – | OE | R | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – – | OE | OE | – – – | OE | R | ||
| Sarake Yhteensä | C | – – – | C | – – | C | – – | C | n | |
Taulukkoon 11 perustuvan yleisen hypoteesin testitilasto.5 ”Päivitetty yleinen kontingenssitaulukko” sekä ehdot, joiden mukaan se noudattaa khiin neliö -jakaumaa.
Testistatistiikka kahden tekijän riippumattomuuden testaamiseksi
χ2=Σ(O-E)2E
jossa summa on taulukon kaikkien ydinsolujen yli.
Jos
- kaksi tutkimustekijää ovat riippumattomia ja
- taulukon 11.5 ”Päivitetty yleinen kontingenssitaulukko” jokaisen solun havaittu lukumäärä O on vähintään 5,
tällöin χ2 noudattaa likimain khiin neliö -jakaumaa, jonka vapausasteet ovat df=(I-1)×(J-1).
Testin suorittamiseen, joka on aina oikeanpuoleinen, käytetään samoja viisivaiheisia menettelyjä, joko kriittisen arvon lähestymistapaa tai p-arvon lähestymistapaa, jotka esiteltiin luvun 8 ”Hypoteesien testaaminen” jaksossa 8.1 ”Hypoteesien testaamisen elementit” ja jaksossa 8.3 ”Testin havaittu merkitsevyys”.
Esimerkki 1
Tutkija haluaa tutkia, onko opiskelijoiden tuloksilla korkeakoulun pääsykokeessa (CEE) mitään viitteellistä voimaa tulevaan korkeakoulumenestykseen, jota mitataan keskiarvolla. Toisin sanoen hän haluaa tutkia, ovatko tekijät CEE ja GPA riippumattomia vai eivät. Hän valitsee satunnaisesti n = 100 opiskelijaa eräästä korkeakoulusta ja kirjaa ylös kunkin opiskelijan pistemäärän valintakokeesta sekä hänen arvosanojensa keskiarvon toisen vuoden lopussa. Hän jakaa pääsykokeen pisteet kahteen tasoon ja arvosanojen keskiarvot kolmeen tasoon. Lajittelemalla tiedot näiden jaottelujen mukaan hän muodostaa taulukossa 11.6 esitetyn satunnaisvaihtelutaulukon ”CEE versus GPA Contingency Table”, jossa rivien ja sarakkeiden summat on jo laskettu.
Taulukko 11.6 CEE versus GPA Contingency Table
| GPA | ||||||
|---|---|---|---|---|---|---|
| <2.7 | 2.7 – 3.2 | >3.2 | Rivi Yhteensä | |||
| CEE | <1800 | 35 | 12 | 5 | 52 | |
| ≥1800 | 6 | 24 | 18 | 48 | ||
| Sarake Yhteensä | 41 | 36 | 23 | Total=100 | ||
Test, 1 prosentin merkitsevyystasolla, antavatko nämä tiedot riittävästi näyttöä sen päättelemiseksi, että CEE-pisteet kertovat tulevien korkeakouluopiskelijoiden tulevasta suoritustasosta GPA:lla mitattuna.
Ratkaisu:
Tehdään testi käyttäen kriittisen arvon lähestymistapaa noudattaen tavanomaista viisivaiheista menetelmää, joka on esitetty luvun 8 ”Hypoteesien testaaminen” luvun 8.1 ”Hypoteesien testaamisen elementit” lopussa.
-
Vaihe 1. Hypoteesit ovat
H0:CEE ja GPA ovat riippumattomia tekijöitävs. Ha:CEE ja GPA eivät ole riippumattomia tekijöitä
- Vaihe 2. Jakauma on khiin neliö.
-
Vaihe 3. Jotta voimme laskea testistatistiikan arvon, meidän on ensin laskettava odotettu luku kullekin kuudesta ydinsolusta (ne, joiden merkinnät on lihavoitu):
- 1. rivi ja 1. sarake: E=(R×C)∕n=41×52∕100=21.32
- 1. rivi ja 2. sarake: E=(R×C)∕n=36×52∕100=18.72
- 1. rivi ja 3. sarake: E=(R×C)∕n=23×52∕100=11.96
- 2. rivi ja 1. sarake: E=(R×C)∕n=41×48∕100=19.68
- 2. rivi ja 2. sarake: E=(R×C)∕n=36×48∕100=17.28
- 2. rivi ja 3. sarake: E=(R×C)∕n=23×48∕100=11.04
Taulukko 11.6 ”CEE vs. GPA Contingency Table” on päivitetty taulukoksi 11.7 ”Päivitetty CEE vs. GPA Contingency Table”.
Table 11.7 Päivitetty CEE versus GPA Contingency Table
GPA <2.7 2.7-3.2 >3.2 Rivi Yhteensä CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Sarake Yhteensä C = 41 C = 36 C = 23 n = 100 Testitilasto on
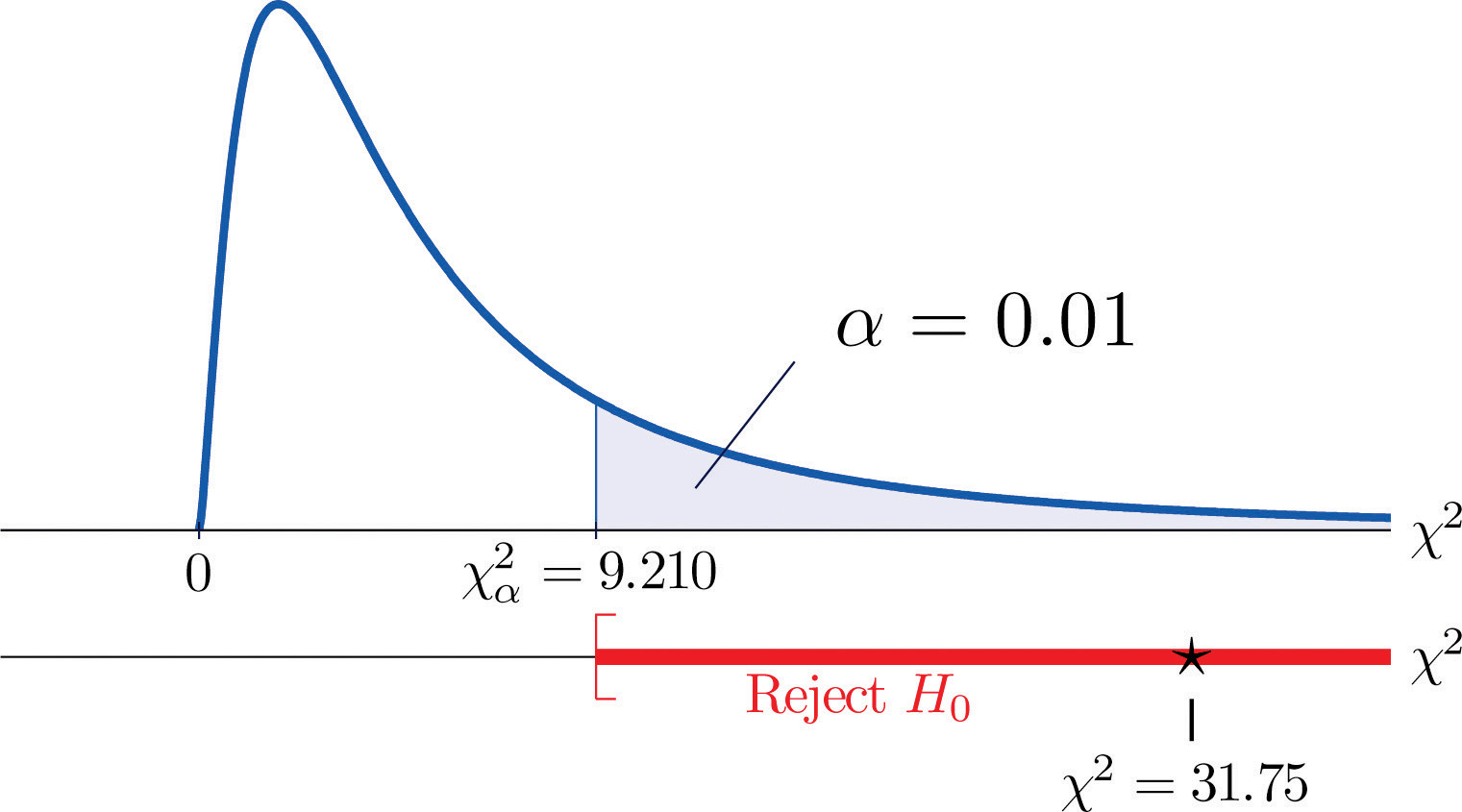
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Koska CEE-tekijällä on kaksi tasoa ja GPA-tekijällä kolme, I = 2 ja J = 3. Näin ollen testistatistiikka noudattaa khiin neliö -jakaumaa, jossa df=(2-1)×(3-1)=2 vapausastetta.
Koska testi on oikeanpuoleinen, kriittinen arvo on χ0.012. Kuviosta 12.4 ”Khiin neliö -jakaumien kriittiset arvot” luettuna χ0.012=9.210, joten hylkäysalue on [9.210,∞).
- Vaihe 5. Koska 31,75 > 9,21, päätös on hylätä nollahypoteesi. Katso kuva 11.4. Aineisto antaa 1 %:n merkitsevyystasolla riittävästi näyttöä päätellä, että CEE-pisteet ja GPA eivät ole riippumattomia: pääsykokeen pistemäärällä on ennustusvoimaa.
Kuvio 11.4 Huomautus 11.9 ”Esimerkki 1”
Keskeisiä johtopäätöksiä
- Kriittiset khiin neliöjakauman arvot vapausasteilla df löytyvät kuviosta 12.4 ”Khiin neliö -jakaumien kriittiset arvot”.
- Khiin neliö -testiKhiin neliö -tilastoon perustuvalla testillä voidaan tarkistaa, ovatko kaksi tekijää riippumattomia. voidaan arvioida hypoteesia, jonka mukaan kaksi satunnaismuuttujaa tai tekijää ovat riippumattomia.
Harjoitukset
-
Löydä χ0.012 jokaiselle seuraavalle vapausasteiden määrälle.
- df=5
- df=11
- df=25
-
Löydä χ0.052 jokaiselle seuraavalle vapausasteiden määrälle.
- df=6
- df=12
- df=30
-
Find χ0.102 jokaiselle seuraavista vapausasteiden lukumääristä.
- df=6
- df=12
- df=30
-
Löydä χ0.012 kullekin seuraavista vapausasteiden lukumääristä.
- df=7
- df=10
- df=20
-
For df=7 and α=0.05, find
- χα2
- χα22
-
For df=17 and α=0.01, löydä
- χα2
- χα22
-
Aineiston otos on lajiteltu 2 × 2 -kontingenssitaulukkoon kahden faktorin perusteella, joilla kummallakin on kaksi tasoa.
Tekijä 1 Taso 1 Taso 2 Rivi yhteensä Tekijä 2 Taso 1 20 10 R Taso 2 15 5 R Sarakkeiden yhteissumma C C n - Löydä sarakkeiden yhteissummat, taulukon rivisummat ja kokonaissumma n.
- Löydä kunkin solun odotettu havaintojen lukumäärä E, joka perustuu oletukseen, että kaksi tekijää ovat riippumattomia (eli käytä vain kaavaa E=(R×C)∕n).
- Löydä khiin neliö -testistatistiikan χ2 arvo.
- Löydä khiin neliö -testistatistiikan vapausasteiden lukumäärä.
-
Datanäyte on lajiteltu 3 × 2 -kontingenssitaulukkoon kahden tekijän perusteella, joista toisella on kolme tasoa ja toisella kaksi tasoa.
Tekijä 1 Taso 1 Taso 2 Rivi yhteensä Tekijä 2 Taso 1 20 10 R Taso 2 15 5 R Taso 3 10 20 R Sarakkeen loppusumma C C C n - Löydä sarakkeiden loppusummat, taulukon rivisummat ja kokonaissumma n.
- Löydä kunkin solun odotettu havaintojen lukumäärä E, joka perustuu oletukseen, että kaksi tekijää ovat riippumattomia (eli käytä vain kaavaa E=(R×C)∕n).
- Löydä khiin neliö -testistatistiikan χ2 arvo.
- Löydä khiin neliö -testistatistiikan vapausasteiden lukumäärä.
Basic
-
Lastenpsykologi uskoo, että lapset suoriutuvat testeistä paremmin, kun heille annetaan koettu valinnanvapaus. Tämän uskomuksen testaamiseksi psykologi suoritti kokeen, jossa 200 kolmasluokkalaista lasta jaettiin satunnaisesti kahteen ryhmään, A ja B. Jokaiselle lapselle annettiin sama yksinkertainen logiikkatesti. Ryhmässä B jokaiselle lapselle annettiin kuitenkin vapaus valita tekstivihko monista, joiden kansissa oli erilaisia piirroksia. Kunkin lapsen suoritus arvioitiin erittäin hyväksi, hyväksi ja tyydyttäväksi. Tuloksista on yhteenveto oheisessa taulukossa. Testaa 5 prosentin merkitsevyystasolla, onko aineistossa riittävästi näyttöä psykologin uskomuksen tueksi.
Ryhmä A B Suoriutuminen Erittäin hyvä 32 29 Hyvä 55 61 Hyvä 10 13 -
Viininmaistelukilpailujen osalta, monet asiantuntijat väittävät, että ensimmäinen lasillinen tarjoiltua viiniä asettaa vertailumakua ja että erilainen vertailuviini voi muuttaa muiden kilpailussa olevien viinien suhteellista sijoitusta. Tämän väitteen testaamiseksi viininmaistelutilaisuudessa tarjoiltiin kolme viiniä, A, B ja C. Jokaiselle henkilölle tarjoiltiin yksi lasillinen kutakin viiniä, mutta eri järjestyksessä eri vieraille. Lopuksi kutakin henkilöä pyydettiin nimeämään paras näistä kolmesta. Tilaisuudessa oli mukana sata seitsemänkymmentäkaksi henkilöä, ja heidän parhaimmat valintansa on esitetty oheisessa taulukossa. Testaa 1 prosentin merkitsevyystasolla, onko aineistossa riittävästi todisteita sen väitteen tueksi, että viiniasiantuntijoiden mieltymys riippuu ensimmäiseksi tarjoillusta viinistä.
Top Pick A B C Ensimmäinen lasi A 12 31 27 B 15 40 21 C 10 9 7 -
On jätetty-Vasemmankätisyys on perinnöllistä? Tähän kysymykseen vastaamiseksi valitaan satunnaisesti 250 aikuista, joiden kätisyys ja vanhempien kätisyys kirjataan ylös. Tulokset on koottu yhteen oheiseen taulukkoon. Testaa 1 prosentin merkitsevyystasolla, onko aineistossa riittävästi todisteita, joiden perusteella voidaan päätellä, että kätisyys on perinnöllistä.
Vanhempien määrä vasen- Oikea 178 21 21 -
Jotkut geenitutkijat väittävät, että vasemmanpuoleisen käden määräävät geenit-kätisyyden määräävät myös aivojen kielikeskusten kehitystä. Jos tämä väite pitää paikkansa, olisi kohtuullista odottaa, että vasenkätisillä ihmisillä on yleensä vahvemmat kielelliset kyvyt. Tutkimuksessa, jonka tarkoituksena oli tutkia tätä väitettä, valittiin satunnaisesti 807 opiskelijaa, jotka osallistuivat Graduate Record Examination (GRE) -tutkintoon. Heidän pistemääränsä kokeen kieliosiossa luokiteltiin kolmeen luokkaan: heikko, keskinkertainen ja korkea, ja myös heidän kätisyytensä kirjattiin ylös. Tulokset esitetään oheisessa taulukossa. Testaa 5 prosentin merkitsevyystasolla, onko aineistossa riittävästi todisteita, joiden perusteella voidaan päätellä, että vasenkätisillä on yleensä vahvempi kielitaito.
GRE-englannin pisteet matala keskiarvo korkea Kätisyys vasen 18 40 22 Oikea 201 360 166 -
Yleisesti uskotaan, että vakaassa perheessä kasvaneilla lapsilla on taipumus pärjätä koulussa. Tämän uskomuksen todentamiseksi eräs yhteiskuntatieteilijä tutki 290 satunnaisesti valitun oppilaan tiedot julkisessa lukiossa ja merkitsi muistiin kunkin oppilaan perherakenteen ja akateemisen aseman neljä vuotta lukioon tulon jälkeen. Tämän jälkeen tiedot lajiteltiin 2 × 3 kontingenssitaulukkoon, jossa oli kaksi tekijää. Tekijässä 1 on kaksi tasoa: valmistunut ja ei valmistunut. Faktorissa 2 on kolme tasoa: ei vanhempia, yksi vanhempi ja kaksi vanhempaa. Tulokset esitetään oheisessa taulukossa. Testaa 1 prosentin merkitsevyystasolla, onko aineistossa riittävästi todisteita, joiden perusteella voidaan päätellä, että perherakenteella on merkitystä oppilaiden koulumenestykseen.
Academic Status Graduated Did Not Graduate PERHE Ei vanhempaa 18 31 yksi vanhempi 101 44 Kaksi vanhempaa 70 26 -
Suuren yläkoulun ylläpitäjä toivoo, että hän käyttäisi julkkisten vaikutusvaltaa rohkaistakseen koululaisia terveellisempiin valintoihin koulun ruokalassa. Kahvila sijaitsee keskellä avointa tilaa. Joka päivä lounasaikaan oppilaat saavat lounaansa ja juomansa kolmessa erillisessä jonossa, jotka johtavat kolmelle erilliselle tarjoiluasemalle. Koulun ylläpitäjä näytti kokeeksi julisteen, jossa suosittu teini-ikäinen poptähti juo maitoa jokaisessa kolmessa paikassa, joissa juomia tarjotaan, paitsi että julisteessa oleva maito on erilaista jokaisessa paikassa: yhdessä on valkoista maitoa, toisessa mansikanmakuista vaaleanpunaista maitoa ja toisessa suklaamaitoa. Ensimmäisen kokeilupäivän jälkeen valvoja merkitsi oppilaiden maitovalinnat erikseen kolmella rivillä. Tiedot on esitetty oheisessa taulukossa. Testaa 1 prosentin merkitsevyystasolla, onko aineistossa riittävästi todisteita, joiden perusteella voidaan päätellä, että julisteilla oli jonkinlainen vaikutus oppilaiden juomavalintoihin.
Opiskelijan valinta Säännöllinen Mansikka Suklaa Poster Choice Säännöllinen 38 28 40 Mansikka 18 18 51 24 Suklaa 32 32 32 53
Sovellukset
-
Suuri Tietosarja 8 tallentaa 300:lle satunnaisesti valitulle aikuiselle, jotka käyvät säännöllisesti elokuvateattereissa, tehdyn tutkimuksen tulokset. Jokaisesta henkilöstä kirjattiin sukupuoli ja mieluisin elokuvatyyppi. Testaa 5 %:n merkitsevyystasolla, onko aineistossa riittävästi todisteita, joiden perusteella voidaan päätellä, että tekijät ”sukupuoli” ja ”mieluisin elokuvatyyppi” ovat riippuvaisia toisistaan.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Suuret. Tietosarjaharjoitus
Vastaukset
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n=50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5.99, ei hylätä H0
-
χ2=72.35, χ0.012=9.21, hylätään H0
-
χ2=21.2784, χ0.012=9.21, hylätään H0
-
χ2=28.4539. df=3. Hylkäysalue: [7.815,∞). Päätös:
.