Függetlenségvizsgálatok
A könyvben korábban már találkoztunk hipotézisvizsgálatokkal, amelyek azzal foglalkoztak, hogy két populációs paraméter számértékeit hogyan hasonlítják össze. Ebben az alfejezetben olyan hipotéziseket fogunk vizsgálni, amelyeknek ahhoz van közük, hogy két véletlen változó függetlenül veszi-e fel az értékét, vagy az egyik értéke kapcsolatban áll a másik értékével. A hipotéziseket tehát szavakkal fogjuk kifejezni, nem pedig matematikai szimbólumokkal. A vitát a következő példa köré építjük:
Egy elmélet szerint az anyaméhben lévő baba neme összefügg a baba szívritmusával: a kislányok szívritmusa általában magasabb. Tegyük fel, hogy ezt az elméletet szeretnénk tesztelni. Megvizsgáljuk 40 csecsemő szívfrekvencia-felvételét, amelyeket anyjuk utolsó, szülés előtti terhesgondozásakor készítettek, és mind a 40 véletlenszerűen kiválasztott felvételhez kiszámítjuk két véletlenszerű mérték értékét: 1) a nem és 2) a szívfrekvencia. Ebben az összefüggésben ezt a két véletlen mérőszámot gyakran nevezik faktoroknakEgy változó, amelynek több minőségi szintje van… Mivel a bizonyítási teher az, hogy a szívfrekvencia és a nem összefügg, nem pedig az, hogy nincs köztük kapcsolat, a baba nemére és a szívfrekvenciára vonatkozó elmélet tesztelésének problémája a következő hipotézisek tesztjeként fogalmazható meg:
H0:A baba neme és a baba szívfrekvenciája függetlenvs. Ha:A baba neme és a baba szívfrekvenciája nem független
A nem tényezőnek két természetes kategóriája vagy szintje van: fiú és lány. A második tényezőt, a szívfrekvenciát két szintre, alacsony és magas szintre osztjuk úgy, hogy valamilyen szívfrekvenciát választunk, mondjuk 145 ütés/perc, mint a kettő közötti határértéket. A 145 ütés/perc alatti pulzusszámot alacsony, a 145-öt és afelettit pedig magas pulzusszámnak tekintjük. A 40 rekordból egy 2 × 2 kontingenciatáblázatot kapunk. A sorok összegének, az oszlopok összegének és a végösszegnek az összekapcsolásával megkapjuk a 11.1. táblázatban látható “A baba neme és a szívfrekvencia” táblázatot. A négy vastag betűs bejegyzés az n = 40-es mintából származó megfigyelések száma. Volt 11 lány alacsony pulzusszámmal, 17 fiú alacsony pulzusszámmal, és így tovább. Ezek alkotják a kibővített táblázat magját.
11. táblázat.1 A baba neme és a szívritmus
| Szívritmus | ||||
|---|---|---|---|---|
| alacsony | magas | Sor összesen | ||
| Nem | Lány | 11 | 7 | 18 |
| Fiú | 17 | 5 | 22 | |
| Oszlop összesen | 28 | 12 | összesen = 40 | |
Azzal a ténnyel analóg módon, hogy független események valószínűsége az egyes események valószínűségeinek szorzata, ha a szívfrekvencia és a nem függetlenek lennének, akkor azt várnánk, hogy az egyes magcellákban lévő szám közel azonos legyen az azt tartalmazó sor és oszlop R összegének és C összegének szorzatával, osztva az n mintamérettel. Jelölve egy ilyen várható megfigyelések számát E-vel, ez a négy várható érték:
- 1. sor és 1. oszlop: E=(R×C)∕n=18×28∕40=12,6
- 1. sor és 2. oszlop: E=(R×C)∕n=18×12∕40=5,4
- 2. sor és 1. oszlop: E=(R×C)∕n=18×12∕40=5,4
- 2: E=(R×C)∕n=22×28∕40=15,4
- 2. sor és 2. oszlop: E=(R×C)∕n=22×12∕40=6,6
A 11.1. táblázatot “A baba neme és a szívritmus” úgy frissítjük, hogy minden várható értéket a megfelelő magcellába helyezünk, közvetlenül a cellában lévő megfigyelt érték alá. Így kapjuk a frissített 11.2. táblázatot “A baba neme és szívritmusa” című táblázatot.
11. táblázat.2 Frissített baba neme és szívritmus
| Szívritmus | ||||
|---|---|---|---|---|
| alacsony | magas | Sor összesen | ||
| Gender | Lány | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Fiú | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| oszlop Összesen | C = 28 | C = 12 | n = 40 | |
Az egyes magcellákban lévő számok különbségének négyzetösszegével mérhető, hogy az adatok mennyire térnek el attól, amit akkor várnánk, ha a tényezők valóban függetlenek lennének, vagy, standardizálva úgy, hogy minden egyes négyzetet elosztunk a cellában lévő várható számmal, a Σ(O-E)2∕E összeg. A nullhipotézist, miszerint a faktorok függetlenek, csak akkor utasítanánk el, ha ez a szám nagy, tehát a teszt jobb végű. Ebben a példában a Σ(O-E)2∕E véletlen változónak egy szabadsági fokú chi-négyzet eloszlása van. Ha eleve úgy döntöttünk volna, hogy 10%-os szignifikanciaszinten tesztelünk, akkor a 12.4. ábra “Chi-négyzet eloszlások kritikus értékei” című fejezetéből kiolvasva a visszautasítási tartományt meghatározó kritikus érték χα2=χ0,102=2,706 lenne, tehát a visszautasítási tartomány a [2,706,∞) intervallum lenne. Ha kiszámítjuk a standardizált tesztstatisztika értékét, akkor
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Mivel 1,231 < 2,706, a döntés nem a H0 elutasítása. Lásd a 11.3. ábrát “A baba nemének előrejelzése”. Az adatok 10%-os szignifikanciaszinten nem szolgáltatnak elegendő bizonyítékot ahhoz, hogy arra a következtetésre jussunk, hogy a szívfrekvencia és a nem összefügg.
11.3. ábra: A baba nemének előrejelzése
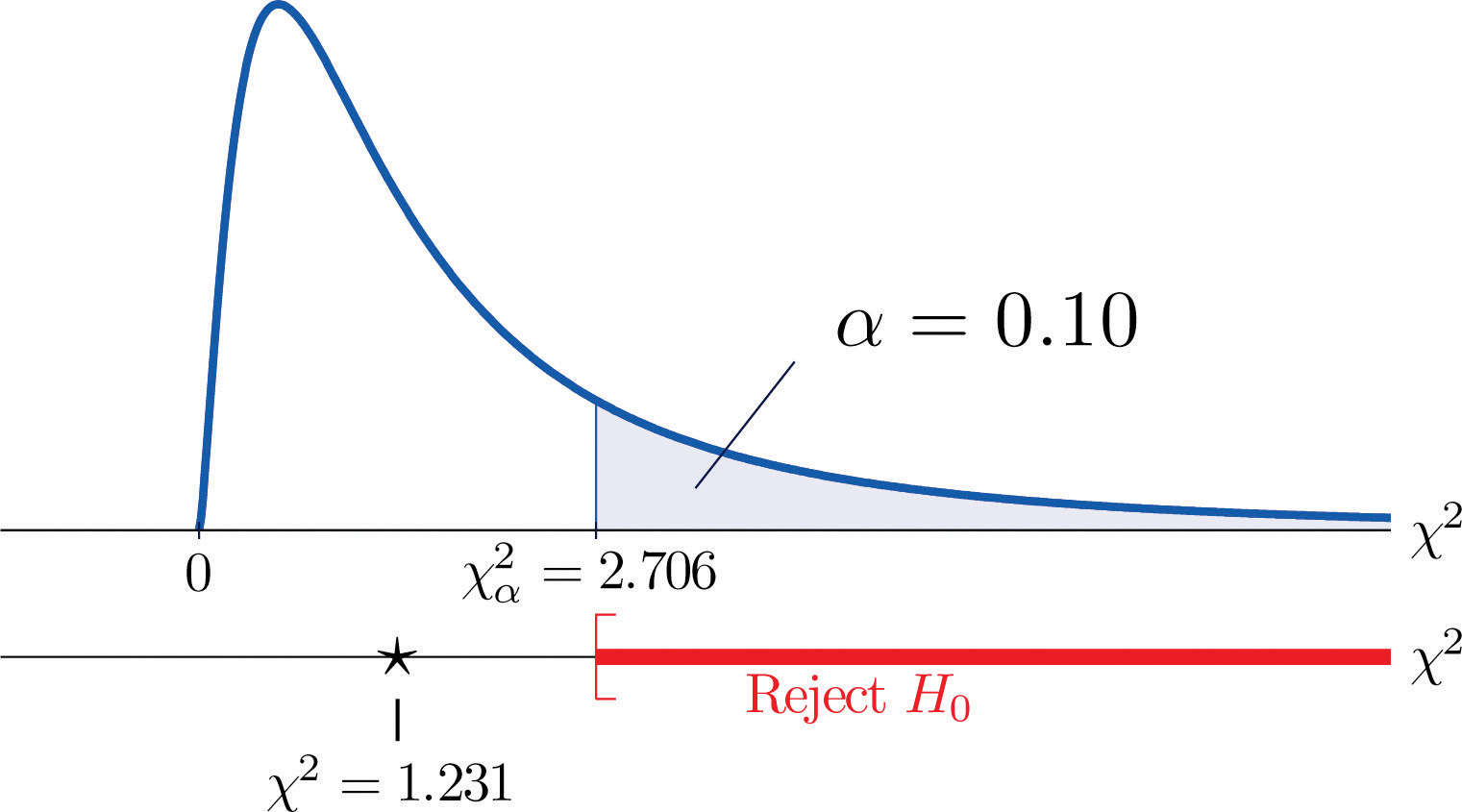
Ezt a konkrét példát szem előtt tartva most térjünk rá az általános helyzetre. Két faktor függetlenségének tesztelésének általános beállításában, nevezzük őket 1. és 2. faktornak, a tesztelendő hipotézisek a következők
H0:A két faktor függetlenvs. Ha:A két faktor nem független
A példában minden faktor több kategóriára vagy szintre van osztva. Ezek adódhatnak természetes módon, mint a fiú-lány nemek felosztása, vagy némileg önkényesen, mint a pulzusszám magas-alacsony felosztása. Tegyük fel, hogy az 1. faktornak I szintjei vannak, a 2. faktornak pedig J szintjei. Ekkor a véletlenszerű mintából származó információ egy általános I × J kontingenciatáblázatot eredményez, amely a 11.3. “Általános kontingenciatáblázat” című táblázatban látható módon jelenik meg a sor- és oszlopösszegekkel, valamint a végösszeggel. Minden egyes cellát egy (i,j) indexpárral lehet jelölni. Oij a cellában az i. sorban és a j. oszlopban lévő megfigyelések megfigyelt számát, Ri az i-edik sorösszeget, Cj pedig a j-edik oszlopösszeget jelöli. A jelölés egyszerűsítése érdekében elhagyjuk az indexeket, így a 11.3. “Általános véletlenszerűségi táblázat” táblázatból a 11.4. “Egyszerűsített általános véletlenszerűségi táblázat” táblázat lesz. Mindazonáltal fontos szem előtt tartani, hogy az Os, az Rs és a Cs, bár ugyanazokkal a szimbólumokkal jelölik őket, valójában különböző számok.
11. táblázat.3 Általános kontingenciatáblázat
| Faktor 2 szintek | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Sor összesen | ||||
| Faktor 1 szintek | 1 | O11 | – – – | O1j | – – – | O1J | – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | Oi1 | – – – | Oij | – – – | OiJ | Ri | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OI1 | – – – | OIj | – – – | OIJ | RI | |||
| Oszlop összesen | C1 | – – – | Cj | – – – – | CJ | n | |||
11. táblázat.4 Egyszerűsített általános valószínűségi táblázat
| Faktor 2 szintek | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Sor összesen | |||
| Faktor 1 szintek | 1 | O | – – – | O | – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – | O | – – – | O | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | O | – – – | O | – – – | O | R | ||
| Egy oszlop összesen | C | C | – – – | C | – – – | C | n | |
Mint a példában, a táblázat minden egyes magcellájára kiszámítjuk, hogy mi lenne a megfigyelések várható száma E, ha a két tényező független lenne. Az E-t a 11.4. “Egyszerűsített általános véletlenszerűségi táblázat” táblázat minden egyes magcellájára (minden olyan cella, amelyben egy O van) a példában alkalmazott szabály szerint számítjuk ki:
ahol R a cellának megfelelő sorösszeg és C az oszlopösszeg, n pedig a minta mérete.
Miután minden cellára kiszámítottuk a várható számot, a 11.4. “Egyszerűsített általános véletlenszerűségi táblázat” táblázatot frissítjük a 11.5. “Frissített általános véletlenszerűségi táblázat” táblázattá úgy, hogy az E kiszámított értékét beillesztjük minden egyes magcellába.
A 11. táblázat.5. Frissített általános függőségi táblázat
| Faktor 2. szintek | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Sor összesen | ||||
| Faktor 1 szintek | 1 | OE | – – – | OE | – – – | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | OE | – – – | OE | – – – | OE | R | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OE | – – – | OE | OE | – – – | OE | R | ||
| Oszlop összesen | C | – – – | C | – – | C | – – | C | n | |
Itt az általános hipotézis tesztstatisztikája a 11. táblázat alapján.5 “Frissített általános kontingenciatáblázat”, azzal a feltétellel együtt, hogy az chi-négyzet eloszlást kövesse.
Tesztstatisztika két tényező függetlenségének tesztelésére
χ2=Σ(O-E)2E
ahol az összeg a táblázat összes magcellájára vonatkozik.
Ha
- a két vizsgálati tényező független, és
- a 11.5. táblázat “Frissített általános kontingencia táblázat” minden egyes cellájának megfigyelt O száma legalább 5,
akkor χ2 megközelítőleg egy chi-négyzet eloszlást követ df=(I-1)×(J-1) szabadságfokokkal.
A hipotézisek tesztelése című 8. fejezet “A hipotézisvizsgálat elemei” című 8.1. szakaszban és “A teszt megfigyelt szignifikanciája” című 8.3. szakaszban bemutatott ötlépéses eljárásokkal – a kritikus érték megközelítéssel vagy a p-érték megközelítéssel – végezzük el a tesztet, amely mindig jobbos végű.
1. példa
Egy kutató azt szeretné megvizsgálni, hogy a diákok főiskolai felvételi vizsgán (CEE) elért pontszámai rendelkeznek-e valamilyen indikáló erővel a GPA-val mért jövőbeli főiskolai teljesítményre vonatkozóan. Más szóval, azt szeretné megvizsgálni, hogy a CEE és a GPA tényezők függetlenek-e vagy sem. Véletlenszerűen kiválasztja egy főiskola n = 100 hallgatóját, és feljegyzi minden egyes hallgató felvételi vizsgán elért pontszámát és a második év végi tanulmányi átlagát. A felvételi vizsgaeredményeket két szintre, a jegyátlagokat pedig három szintre osztja. Az adatokat e felosztások szerint rendezve megalkotja a 11.6. táblázatban látható “CEE versus GPA Contingency Table” (CEE versus GPA Contingency Table) kontingencia táblázatot, amelyben a sor- és oszlopösszegek már kiszámításra kerültek.
11.6. táblázat CEE versus GPA Contingency Table
| GPA | |||||
|---|---|---|---|---|---|
| <2,7 | 2,7-től 3,2-ig | >3.2 | Sor összesen | ||
| CEE | <1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Oszlop összesen | 41 | 36 | 23 | Total=100 | |
Teszt, az 1%-os szignifikanciaszinten, hogy ezek az adatok elegendő bizonyítékot szolgáltatnak-e annak megállapításához, hogy a CEE pontszámok jelzik a bejövő főiskolai elsőévesek jövőbeli teljesítményszintjét a tanulmányi átlaggal mérve.
Megoldás:
A tesztet a kritikus érték megközelítésével végezzük el, a 8. fejezet “Hipotézisek tesztelése” című fejezet “A hipotézisvizsgálat elemei” című 8.1. szakaszának végén ismertetett szokásos ötlépéses módszert követve.
-
1. lépés. A hipotézisek a következők
H0:A CEE és a GPA független tényezőkvs. Ha:A CEE és a GPA nem független tényezők
- 2. lépés. Az eloszlás chi-négyzet.
-
3. lépés. A tesztstatisztika értékének kiszámításához először ki kell számítanunk a várható számot mind a hat magcellára (azokra, amelyeknek a bejegyzései félkövérrel vannak írva):
- 1. sor és 1. oszlop: E=(R×C)∕n=41×52∕100=21,32
- 1. sor és 2. oszlop: E=(R×C)∕n=36×52∕100=18,72
- 1. sor és 3. oszlop: E=(R×C)∕n=23×52∕100=11,96
- 2. sor és 1. oszlop: E=(R×C)∕n=41×48∕100=19,68
- 2. sor és 2. oszlop: E=(R×C)∕n=36×48∕100=17,28
- 2. sor és 3. oszlop: E=(R×C)∕n=23×48∕100=11,04
A 11.6. táblázat “CEE kontra GPA Véletlenszerűségi táblázat” frissül a 11.7. táblázat “Frissített CEE kontra GPA Véletlenszerűségi táblázat”-ra.
A 11. táblázat.7 Frissített CEE versus GPA Contingency Table
GPA <2.7 2.7-3,2 >3,2 Sor összesen CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 oszlop Összesen C = 41 C = 36 C = 23 n = 100 A tesztstatisztika
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Mivel a CEE faktornak két szintje van, a GPA faktornak pedig három, I=2 és J=3. Így a tesztstatisztika a chi-négyzet eloszlást követi, df=(2-1)×(3-1)=2 szabadsági fokkal.
Mivel a teszt jobb végű, a kritikus érték χ0,012. A 12.4. ábra “Chi-négyzet eloszlások kritikus értékei” című részéből olvasva χ0,012=9,210, tehát a visszautasítási tartomány [9,210,∞).
- 5. lépés. Mivel 31,75 > 9,21 a döntés a nullhipotézis elutasítása. Lásd a 11.4. ábrát. Az adatok 1%-os szignifikancia szinten elegendő bizonyítékot szolgáltatnak ahhoz a következtetéshez, hogy a CEE pontszám és a GPA nem függetlenek: a felvételi vizsga pontszámának előrejelző ereje van.
11.4. ábra 11.9. megjegyzés “1. példa”
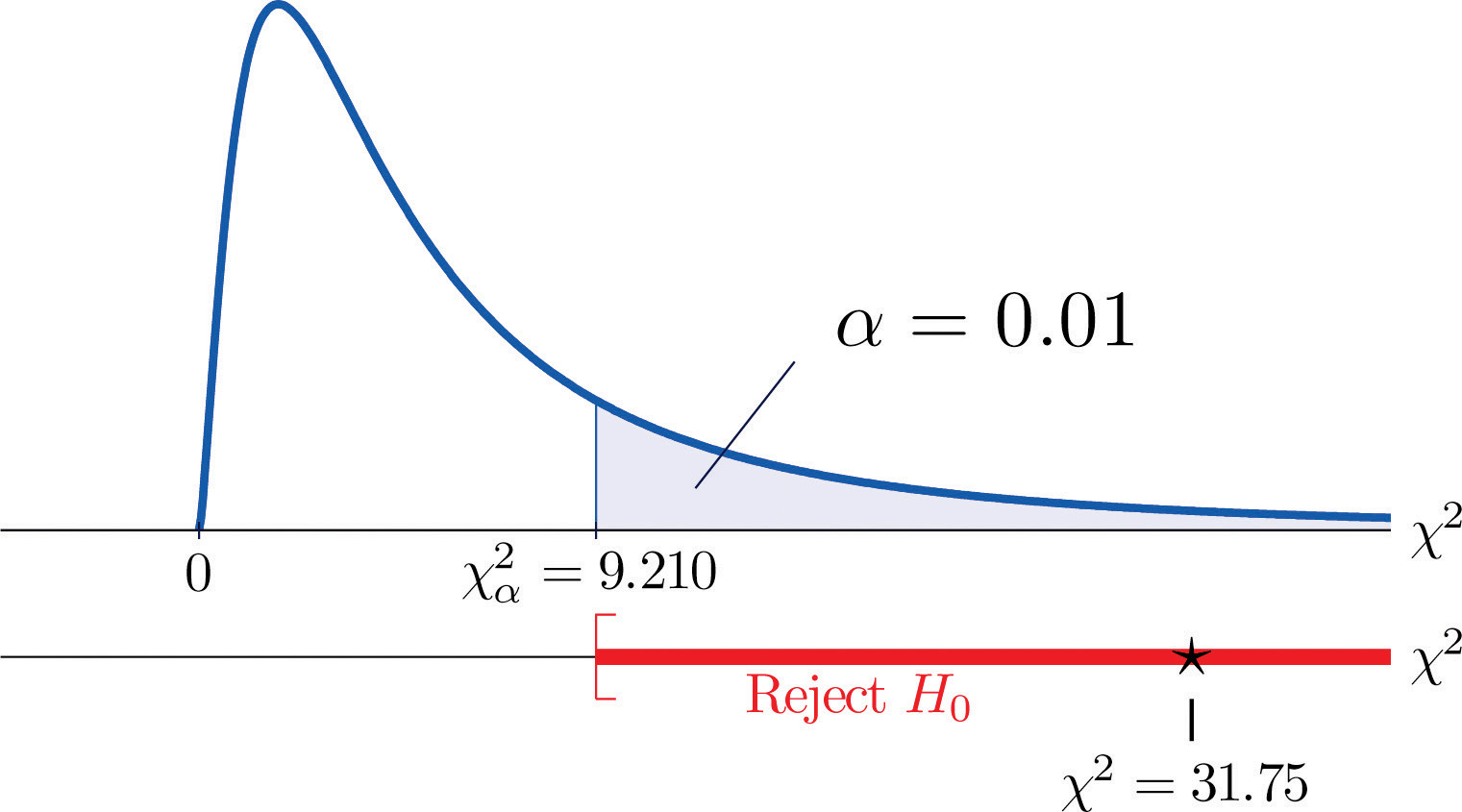
Főbb tanulságok
- A df szabadságfokú khi-négyzet eloszlás kritikus értékei a 12. ábrán találhatók.4 “Chi-négyzet eloszlások kritikus értékei”.
- A chi-négyzet tesztA chi-négyzet statisztikán alapuló teszt annak ellenőrzésére, hogy két tényező független-e. Annak a hipotézisnek az értékelésére használható, hogy két véletlen változó vagy tényező független.
GYakorlatok
-
Keresd meg χ0,012-t az alábbi szabadságfokok számának mindegyikére.
- df=5
- df=11
- df=25
-
Keresd meg χ0,052-t az alábbi szabadságfokok számának mindegyikére.
- df=6
- df=12
- df=30
-
Keresd meg χ0.102 az alábbi szabadságfokok számának mindegyikére.
- df=6
- df=12
- df=30
-
Keresd meg χ0.012 az alábbi szabadságfokok számának mindegyikére.
- df=7
- df=10
- df=20
-
A df=7 és α=0 esetén.05, find
- χα2
- χα22
-
For df=17 and α=0.01, találd
- χα2
- χα22
-
Az adatmintát egy 2 × 2 kontingenciatáblába soroltuk két faktor alapján, amelyeknek mindegyike két szintje van.
1. faktor 1. szint Szint 2 Sor összesen Tényező 2 Szint 1 20 10 R Szint 2 15 5 R Oszlopösszeg C C C n - Megtalálja az oszlopösszegeket, a sorok összegét és a táblázat n végösszegét.
- Következtessük az egyes cellákhoz tartozó megfigyelések várható számát E azon feltételezés alapján, hogy a két tényező független (vagyis egyszerűen használjuk az E=(R×C)∕n képletet).
- Következtessük a chi-négyzet tesztstatisztika χ2 értékét.
- Keresd meg a chi-négyzet tesztstatisztika szabadságfokainak számát.
-
Az adatmintát egy 3 × 2 kontingenciatáblába soroljuk két faktor alapján, amelyek közül az egyiknek három szintje van, a másiknak pedig két szintje.
1. faktor 1. szint 2. szint .
Sor összesen Faktor 2 Szint 1 20 10 R Szint 2 15 5 R Szint 3 10 20 R Oszlopösszeg C C C n - Megtalálja az oszlopösszegeket, a sorok összegét és a táblázat n végösszegét.
- Következtessük az egyes cellákhoz tartozó megfigyelések várható számát E azon feltételezés alapján, hogy a két tényező független (vagyis egyszerűen használjuk az E=(R×C)∕n képletet).
- Következtessük a chi-négyzet tesztstatisztika χ2 értékét.
- Keresd meg a khi-négyzet tesztstatisztika szabadságfokainak számát.
Bázis
-
Egy gyermekpszichológus szerint a gyerekek jobban teljesítenek a teszteken, ha vélt választási szabadságot kapnak. Ennek a meggyőződésnek a tesztelésére a pszichológus egy olyan kísérletet végzett, amelyben 200 harmadik osztályos gyermeket véletlenszerűen két csoportba osztottak, A és B. Mindegyik gyermek ugyanazt az egyszerű logikai tesztet kapta. A B csoportban azonban minden gyermek szabadon választhatott egy szöveges füzetet a sok közül, amelyeknek a borítóján különböző rajzok voltak. Az egyes gyermekek teljesítményét nagyon jó, jó és közepes minősítéssel értékelték. Az eredményeket a mellékelt táblázatban foglaltuk össze. Vizsgálja meg 5%-os szignifikanciaszinten, hogy az adatok elegendő bizonyítékot tartalmaznak-e a pszichológus meggyőződésének alátámasztására.
Group A B Teljesítmény Nagyon jó 32 29 .
Jó 55 61 Megfelelő 10 13 -
A borkóstoló versenyek tekintetében, sok szakértő azt állítja, hogy az első pohár felszolgált bor meghatározza a referencia ízt, és egy eltérő referencia bor megváltoztathatja a többi versenyben szereplő bor relatív rangsorát. Ennek az állításnak a tesztelésére egy borkóstoló versenyen három bort, A-t, B-t és C-t szolgáltak fel. Minden személynek egy-egy pohárral szolgáltak fel mindegyik borból, de különböző sorrendben a különböző vendégek számára. Záráskor minden személyt megkértek, hogy nevezze meg a három közül a legjobbat. Százhetvenkét ember vett részt a rendezvényen, és a legjobb választásaikat a mellékelt táblázat tartalmazza. Vizsgálja meg 1%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokban annak az állításnak az alátámasztására, hogy a borszakértők preferenciája az elsőként felszolgált bortól függ.
Top Pick A B B C Első üveg A 12 31 27 B 15 40 21 C 10 9 7 -
Ez marad-öröklődik? A kérdés megválaszolásához 250 felnőttet választanak ki véletlenszerűen, és feljegyzik a kéztartásukat és a szüleik kéztartását. Az eredményeket a mellékelt táblázatban foglaltuk össze. Vizsgálja meg 1%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokból arra a következtetésre, hogy a balkezességnek van-e örökletes eleme.
Szülők száma balkezes-Handed 0 1 2 Handedness Left 8 10 12 Jobb 178 21 21 -
Néhány genetikus azt állítja, hogy a balkezességet meghatározó génekbalkezességet meghatározó tényezők az agy nyelvi központjainak fejlődését is irányítják. Ha ez az állítás igaz, akkor ésszerű lenne azt várni, hogy a balkezesek általában erősebb nyelvi képességekkel rendelkeznek. Egy tanulmány, amelynek célja ennek az állításnak a megfogalmazása volt, véletlenszerűen kiválasztott 807 diákot, akik részt vettek a Graduate Record Examination (GRE) vizsgán. A vizsga nyelvi részében elért pontszámukat három kategóriába sorolták: alacsony, átlagos és magas, és feljegyezték a balkezességüket is. Az eredményeket a mellékelt táblázat tartalmazza. Vizsgálja meg 5%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokból arra a következtetésre, hogy a balkezesek általában erősebb nyelvi képességekkel rendelkeznek.
GRE angol pontszámok alacsony átlag .
magas Kézügyesség bal 18 40 22 Jobb 201 360 166 -
Az általános vélekedés szerint a stabil családban nevelkedő gyerekek általában jól teljesítenek az iskolában. Ennek a hiedelemnek az igazolására egy társadalomtudós 290 véletlenszerűen kiválasztott diák adatait vizsgálta meg egy állami középiskolában, és négy évvel a középiskolába lépés után feljegyezte az egyes diákok családszerkezetét és tanulmányi helyzetét. Az adatokat ezután egy 2 × 3 kontingenciatáblába rendezték, két faktorral. Az 1. faktornak két szintje van: érettségizett és nem érettségizett. A 2. faktornak három szintje van: nincs szülő, egy szülő és két szülő. Az eredményeket a mellékelt táblázat tartalmazza. Vizsgálja meg 1%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokból arra a következtetésre, hogy a családi struktúra befolyásolja a tanulók iskolai teljesítményét.
Academic Status Graduated Did Not Graduated .
Család Nincs szülője 18 31 Egy szülője 101 44 Két szülő 70 26 -
Egy nagy középiskola igazgatója a hírességek befolyását szeretné felhasználni, hogy a diákokat egészségesebb választásra ösztönözze az iskolai menzán. Az ebédlő egy nyitott tér közepén helyezkedik el. Minden nap ebédidőben a diákok három külön sorban kapják meg az ebédet és az italt, amelyek három külön kiszolgáló állomáshoz vezetnek. Kísérletképpen az iskola adminisztrátora egy plakátot helyezett ki egy népszerű tini popsztárról, aki tejet iszik mindhárom helyen, ahol az italokat kínálják, azzal a különbséggel, hogy a plakáton szereplő tej mindegyik helyen más és más: az egyik helyen fehér tej, a másikon eperízű rózsaszín tej, a harmadikon pedig csokoládés tej látható. A kísérlet első napja után az adminisztrátor külön-külön feljegyezte a diákok tejválasztását a három sorban. Az adatokat a mellékelt táblázat tartalmazza. Vizsgálja meg 1%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokból arra a következtetésre, hogy a plakátok valamilyen hatással voltak a diákok italválasztására.
Tanulói választás Szokásos Eper Csokoládé Poszter választás Szokásos 38 28 40 Eper 18 18 51 24 Chocolate 32 32 32 53
Alkalmazások
-
Nagy A 8. adathalmaz egy 300 véletlenszerűen kiválasztott, rendszeresen moziba járó felnőtt megkérdezésének eredményét rögzíti. Minden egyes személy esetében rögzítették a nemet és a preferált filmtípust. Vizsgálja meg 5%-os szignifikanciaszinten, hogy van-e elegendő bizonyíték az adatokban arra a következtetésre, hogy a “nem” és a “preferált filmtípus” tényezők függnek egymástól.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Nagy. Adathalmaz-gyakorlat
Válaszok
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n=50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0,6698, χ0.052=5.99, nem utasítjuk el a H0
-
χ2=72.35, χ0.012=9.21, elutasítjuk a H0
-
χ2=21.2784, χ0.012=9.21, elutasítjuk H0
-
χ2=28.4539. df=3. Elutasítási régió: [7.815,∞). Döntés:
.