Lattiche di Bravais

Scienza >Chimica >Stato solido >Lattiche di Bravais

In questo articolo, studieremo le strutture delle Lattiche di Bravais.

Un cristallo è una porzione omogenea di una sostanza solida fatta di un modello regolare di unità strutturali legate da superfici piane che formano un angolo definito tra loro.

Cella unitaria:

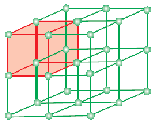
Una cella unitaria è la più piccola unità strutturale ripetuta del solido cristallino (reticolo spaziale). Quando le celle unitarie della stessa sostanza cristallina si ripetono nello spazio in tutte le direzioni, si forma un solido cristallino. La cella unitaria è rappresentata sulla carta disegnando linee che collegano i centri delle particelle costituenti.

La forma geometrica che consiste solo in una serie regolare di punti nello spazio è chiamata reticolo o reticolo spaziale. Può essere definito come una serie di punti che mostrano come molecole, atomi o ioni sono disposti in diversi siti, in uno spazio tridimensionale. Ogni punto all’intersezione delle linee nella cella dell’unità rappresenta la particella costituente, cioè la molecola o l’atomo o lo ione. Questo punto di intersezione delle linee nella cella unitaria è chiamato punto di reticolo o sito di reticolo.

Nota: Ogni punto di reticolo nel reticolo cristallino ha gli stessi dintorni o ambiente. Due o più sostanze cristalline possono avere lo stesso spazio reticolare. Ogni particella nella matrice è sempre rappresentata da un punto di reticolo nella matrice tridimensionale.

Caratteristiche del reticolo cristallino:

• Il reticolo cristallino è una disposizione regolare delle particelle costitutive di un solido cristallino nello spazio tridimensionale.
• Consiste di un gran numero di cellule unitarie.
• Il reticolo cristallino è definito in termini di proprietà della cella unitaria.
• Alla rottura, forma numerose celle unitarie.
• Un reticolo cristallino può essere ottenuto, manipolato e studiato in laboratorio durante gli esperimenti.
• È una proprietà macroscopica.

Caratteristiche della cella unitaria:

• Una cella unitaria è la più piccola unità strutturale ripetuta del solido cristallino.
• È l’unità fondamentale del reticolo cristallino che possiede tutte le proprietà del cristallo.
• La cella unitaria definisce le proprietà fondamentali del reticolo cristallino.
• La cella unitaria è un’unità fondamentale, quindi non può essere divisa ulteriormente.
• La cella unitaria è un concetto ipotetico, quindi non può essere ottenuto durante gli esperimenti.
• È una proprietà microscopica.

Tipi di reticolo spaziale:

Lattice unidimensionale:

In questo reticolo, esiste un insieme di punti disposti a distanze uguali lungo.

Lattice bidimensionale:

In questo tipo, si specificano due lati e l’angolo tra essi. Ci sono cinque tipi di reticolo bidimensionale.

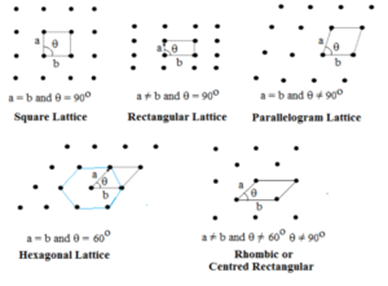
Il reticolo esagonale è un rombo con θ = 60°

Lattici di Bravais:

Lasciamo che le lunghezze dei tre bordi della cella siano a, b e c. Sia α l’angolo tra il lato b e c. Sia β l’angolo tra i lati a e c. Sia γ l’angolo tra i lati a e b.

Il matematico francese Bravais disse che per diversi valori di a, b, c, e α, β, γ, sono possibili al massimo quattordici (14) strutture. Queste disposizioni si chiamano tattiche di Bravais.

14 tattiche di Bravais:

Sr. No.	Cristallo Sistema	Lattice spaziale Tipo	Diagramma	Lunghezze dei bordi	Angoli	Esempi
	Cubico	Semplice primitivo		a = b = c	α = β = γ = 90°	Polonio (Po)
	Cubico	Corpo centrato		a = b = c	α = β = γ = 90°	Iron (Fe), Rubidio (Rb), Sodio (Na), Titanio (Ti), Tungsteno (W), Uranio (U), Zirconio (Zr)
	Cubico	Faccia centrata		a = b = c	α = β = γ = 90°	Rame (Cu), Alluminio (Al), Nichel (Ni), Oro (Au), Argento (Ag), Platino (Pt)
	Tetragono	Semplice primitivo		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonale	Corpo centrato		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Ortorombico	Semplice primitivo		a ≠ b ≠ c	α = β = γ = 90°	Zolfo rombico
	Ortorombico	Corpo centrato		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Ortorombico	Faccia centrata		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Ortorombico	Fine centrato		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monoclino	semplice primitivo		a ≠ b ≠ c	α =γ = 90° e β ≠ 90°	Zolfo monoclino
	Monoclino	Fine centrato		a ≠ b ≠ c	α =γ = 90° e β ≠ 90	Na2SO4. 10H2O
	Triclino	semplice primitivo		a ≠ b ≠ c	α =γ = 90° e β ≠ 90°	K2Cr2O7, H3BO3
	Esagonale	Semplice primitivo		a = b ≠ c	α = β = 90° e γ = 120°	ZnO, BeO, CoS, SnS
	Romboedrico	Semplice primitivo		a ≠ b ≠ c	α = β = γ ≠ 90°	Calcite, NaNO3, FeCO3

Particella all’angolo:

La particella all’angolo della cella unitaria è condivisa da 8 celle unitarie (4 strati sotto e 4 strati sopra). Quindi ogni cella unitaria 1/8 di particella.

Particella sulla faccia:

La particella sulla faccia della cella unitaria è condivisa da 2 celle unitarie adiacenti. Quindi ogni cella unitaria 1/2 particella.

Particella sul bordo:

La particella sul bordo della cella unitaria è condivisa da 4 celle unitarie (2 strati sotto e 2 strati sopra). Quindi ogni cella unitaria 1/4 di particella.

Numero di coordinazione:

Il numero di coordinazione della particella costituente il reticolo cristallino è il numero di particelle che circondano una singola particella in un reticolo cristallino.

Maggiore è il numero di coordinazione più strettamente le particelle sono imballate nel reticolo cristallino. Il numero di coordinazione è la misura della durezza del cristallo.

Numero di particelle nella cella unitaria e numero di coordinazione

Struttura cubica semplice (scc):

Dalla struttura, possiamo vedere che ci sono 8 particelle in 8 angoli della cella unitaria.Ogni particella d’angolo è condivisa da 8 celle unitarie vicine. Quindi ogni cella unitaria contiene 1/8 della particella al suo angolo.
Numero di angoli = 8, quindi numero di particelle nella cella unitaria = 1/8x 8 = 1

Ogni particella in questa struttura è direttamente in contatto con altre quattro particelle nel suo piano e una particella ciascuna nello strato superiore e in quello inferiore. Il numero di coordinazione di Hencet per la struttura cubica semplice è 4+ 1+ 1 = 6

Struttura cubica centrata sul corpo (bcc):

Dalla struttura, possiamo vedere che ci sono 8 particelle in 8 angoli della cella unitaria.Ogni particella d’angolo è condivisa da 8 celle unitarie vicine. Quindi ogni cella unitaria contiene 1/8 della particella al suo angolo. Numero di angoli = 8, quindi numero di particelle nella cella unitaria agli angoli = 1/8 x 8 = 1

Al tempo stesso, c’è un atomo al centro della cella, quindi il numero di particelle nella cella unitaria 1 + 1 = 2

Ogni particella in questa struttura è direttamente in contatto con altre quattro particelle nello strato superiore e quattro particelle nello strato inferiore. Quindi il numero di coordinazione per la struttura cubica centrata sul corpo è 4 + 4 = 8

Struttura cubica centrata sulla faccia (fcc):

Dalla struttura, possiamo vedere che ci sono 8 particelle in 8 angoli della cella unitaria. Ogni particella d’angolo è condivisa da altre 8 celle unitarie vicine. Quindi ogni cella unitaria contiene 1/8 della particella al suo angolo. Il numero di angoli = 8. Quindi il numero di particelle in una cella unitaria agli angoli = 1/8 x 8 = 1

Ci sono 6 particelle a 6 facce della cella unitaria. Ogni particella della faccia è condivisa da 2 celle unitarie vicine. Quindi ogni cella unitaria contiene 1/2 della particella sulla sua faccia.
Il numero di facce = 6. Quindi il numero di particelle sulla faccia = 1/2 x 6 = 3

Quindi numero di particelle nella cella unitaria 1 + 3 = 4

Ogni particella in questa struttura è direttamente in contatto con 4 altre particelle nel suo strato e con 4 particelle nello strato sopra e 4 particelle nello strato sotto. Quindi il numero di coordinazione per la struttura cubica centrata sulla faccia è 4 + 4 + 4 = 12

Note:

Per la particella centrata sul bordo è condiviso da 4 celle unitarie. Quindi ogni cella unitaria consiste di 1/4 di particella Il numero di atomi per cella unitaria è nello stesso rapporto della stechiometria del composto. Quindi aiuta a predire la formula del composto.

Scienza > Chimica > Stato Solido > Lattiche di Bravais