Toetsen voor Onafhankelijkheid
Hypothesetoetsen die we eerder in het boek zijn tegengekomen, hadden te maken met hoe de numerieke waarden van twee populatieparameters zich tot elkaar verhielden. In deze paragraaf zullen wij hypothesen onderzoeken die te maken hebben met de vraag of twee willekeurige variabelen al dan niet onafhankelijk hun waarde aannemen, dan wel of de waarde van de ene een verband heeft met de waarde van de andere. De hypothesen worden dus uitgedrukt in woorden, niet in wiskundige symbolen. We bouwen de discussie op rond het volgende voorbeeld.
Er is een theorie dat het geslacht van een baby in de baarmoeder verband houdt met de hartslag van de baby: babymeisjes hebben meestal een hogere hartslag. Stel dat we deze theorie willen testen. We onderzoeken de hartslaggegevens van 40 baby’s die zijn genomen tijdens de laatste prenatale controles van hun moeders vóór de bevalling, en we berekenen voor elk van deze 40 willekeurig gekozen gegevens de waarden van twee willekeurige maten: 1) geslacht en 2) hartslag. In deze context worden deze twee willekeurige maten vaak factoren genoemdEen variabele met verschillende kwalitatieve niveaus. Aangezien de bewijslast erin bestaat dat hartslag en geslacht met elkaar verband houden, niet dat ze geen verband houden, kan het probleem van de toetsing van de theorie over baby geslacht en hartslag worden geformuleerd als een toetsing van de volgende hypothesen:
H0:Baby geslacht en baby hartslag zijn onafhankelijkvs. Ha:Baby geslacht en baby hartslag zijn niet onafhankelijk
De factor geslacht heeft twee natuurlijke categorieën of niveaus: jongen en meisje. We verdelen de tweede factor, hartslag, in twee niveaus, laag en hoog, door een bepaalde hartslag te kiezen, bijvoorbeeld 145 slagen per minuut, als de grens tussen beide. Een hartslag van minder dan 145 slagen per minuut wordt als laag beschouwd en 145 en meer als hoog. De 40 records geven aanleiding tot een 2 × 2 contingentietabel. Door de rijtotalen, de kolomtotalen en het eindtotaal aan elkaar toe te voegen, krijgen we de tabel in tabel 11.1 “Baby geslacht en hartslag”. De vier vetgedrukte regels zijn tellingen van waarnemingen uit de steekproef van n = 40. Er waren 11 meisjes met een lage hartslag, 17 jongens met een lage hartslag, enzovoort. Zij vormen de kern van de uitgebreide tabel.
Tabel 11.1 Baby Geslacht en Hartslag
| Hartslag | ||||
|---|---|---|---|---|
| Laag | Hoog | Rijtal | ||
| Geslacht | Meisje | 11 | 7 | 18 |
| Boy | 17 | 5 | 22 | |
| Kolom Totaal | 28 | 12 | Totaal = 40 | |
Naar analogie van het feit dat de waarschijnlijkheid van onafhankelijke gebeurtenissen het product is van de waarschijnlijkheden van elke gebeurtenis, als hartslag en geslacht onafhankelijk zijn, zouden we verwachten dat het aantal in elke kerncel ongeveer gelijk is aan het product van het rijtotaal R en het kolomtotaal C van de rij en kolom die de kerncel bevatten, gedeeld door de steekproefgrootte n. Als we zo’n verwacht aantal waarnemingen E noemen, zijn deze vier verwachte waarden:
- 1e rij en 1e kolom: E=(R×C)∕n=18×28∕40=12,6
- 1e rij en 2e kolom: E=(R×C)∕n=18×12∕40=5,4
- 2e rij en 1e kolom: E=(R×C)∕n=22×28∕40=15,4
- 2e rij en 2e kolom: E=(R×C)∕n=22×12∕40=6.6
We werken tabel 11.1 “Baby geslacht en hartslag” bij door elke verwachte waarde in de overeenkomstige kerncel te plaatsen, recht onder de waargenomen waarde in de cel. Dit levert de bijgewerkte tabel 11.2 “Bijgewerkt geslacht en hartslag van de baby” op.
Tabel 11.2 Bijgewerkte tabel 11.2 “Baby geslacht en hartslag”.
| Hartslag | ||||
|---|---|---|---|---|
| Laag | Hoog | Rijtotaal | ||
| Geslacht | Girl | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Boy | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Kolom Totaal | C = 28 | C = 12 | n = 40 | |
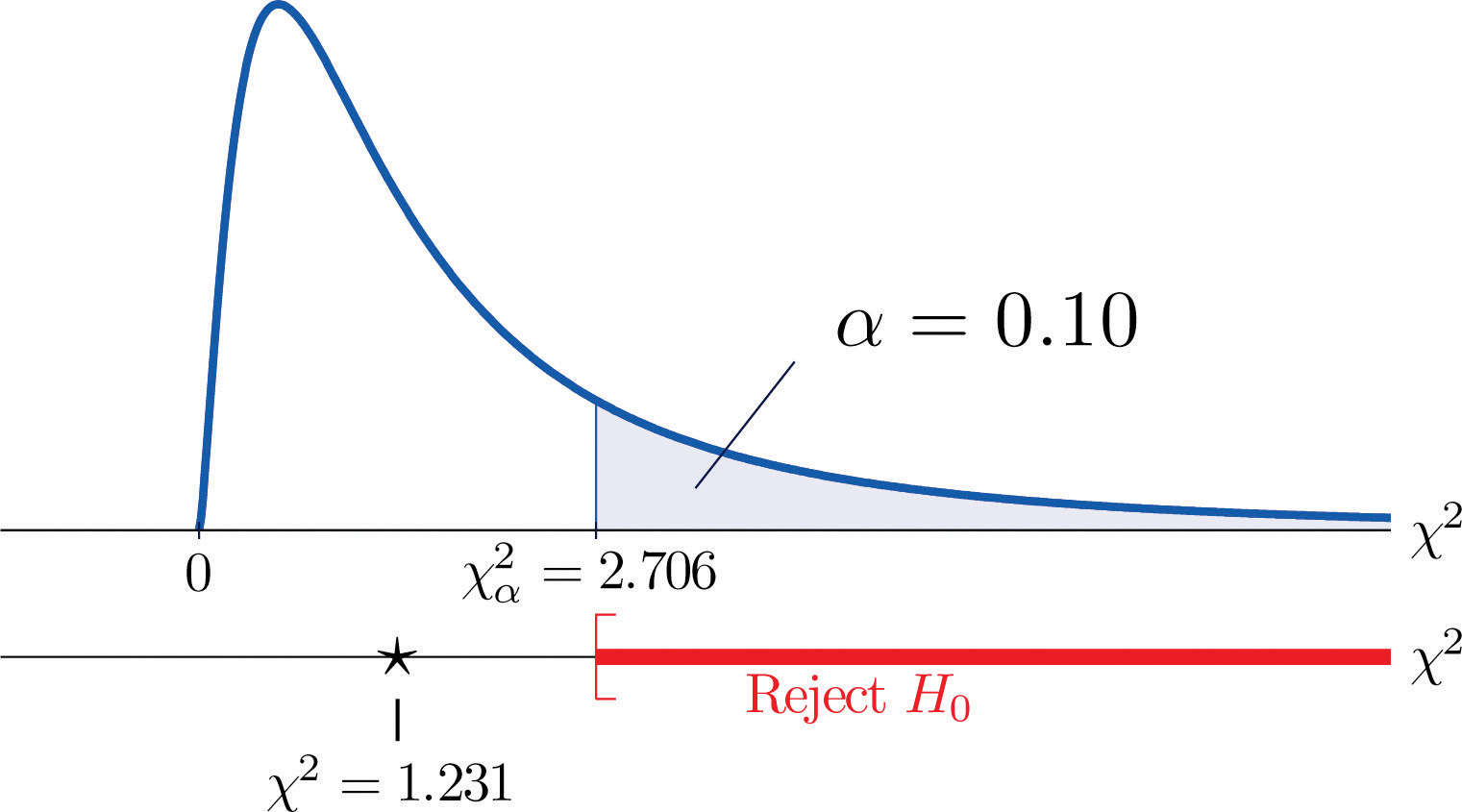
Een maat voor de mate waarin de gegevens afwijken van wat we zouden verwachten als de factoren werkelijk onafhankelijk waren, is de som van de kwadraten van het verschil van de getallen in elke kerncel, of, gestandaardiseerd door elk kwadraat te delen door het verwachte aantal in de cel, de som Σ(O-E)2∕E. De nulhypothese dat de factoren onafhankelijk zijn, wordt alleen verworpen als dit getal groot is, zodat de test een rechtse staart heeft. In dit voorbeeld heeft de willekeurige variabele Σ(O-E)2∕E de chi-kwadraat verdeling met één graad van vrijheid. Indien wij van meet af aan hadden besloten op het 10% significantieniveau te toetsen, zou de kritische waarde die het afwijzingsgebied bepaalt, afgelezen uit figuur 12.4 “Kritische waarden van chi-kwadraatverdelingen”, χα2=χ0.102=2.706 zijn, zodat het afwijzingsgebied het interval [2.706,∞) zou zijn. Wanneer we de waarde van de gestandaardiseerde teststatistiek berekenen, krijgen we
Σ(O-E)2E=(11-12.6)212.6+(7-5.4)25.4+(17-15.4)215.4+(5-6.6)26.6=1.231
Omdat 1.231 < 2.706, wordt besloten H0 niet te verwerpen. Zie figuur 11.3 “Voorspelling van het geslacht van de baby”. De gegevens leveren onvoldoende bewijs, op het 10%-niveau van significantie, om te concluderen dat hartslag en geslacht samenhangen.
Figuur 11.3 Voorspelling van het geslacht van de baby
Met dit specifieke voorbeeld in gedachten, gaan we nu naar de algemene situatie. In de algemene setting van het testen van de onafhankelijkheid van twee factoren, noem ze Factor 1 en Factor 2, zijn de te testen hypotheses
H0:De twee factoren zijn onafhankelijkvs. Ha:De twee factoren zijn niet onafhankelijk
Zoals in het voorbeeld is elke factor onderverdeeld in een aantal categorieën of niveaus. Deze kunnen op natuurlijke wijze ontstaan, zoals bij de verdeling jongen-meisje van het geslacht, of enigszins willekeurig, zoals bij de verdeling hoog-laag van de hartslag. Stel dat Factor 1 niveaus I heeft en Factor 2 niveaus J. Dan geeft de informatie van een aselecte steekproef aanleiding tot een algemene I × J contingentietabel, die er met rijtotalen, kolomtotalen en een eindtotaal zou uitzien als in Tabel 11.3 “Algemene Contingentietabel”. Elke cel kan worden gelabeld door een paar indices (i,j). Oij staat voor het waargenomen aantal waarnemingen in de cel in rij i en kolom j, Ri voor het i-de rijtotaal en Cj voor het j-de kolomtotaal. Om de notatie te vereenvoudigen laten wij de indices weg, zodat Tabel 11.3 “Algemene Contingentietabel” Tabel 11.4 “Vereenvoudigde Algemene Contingentietabel” wordt. Niettemin is het belangrijk voor ogen te houden dat de O’s, de R’s en de C’s, hoewel aangeduid met dezelfde symbolen, in feite verschillende getallen zijn.
Tabel 11.3 Algemene Contingentietabel
| Factor 2 Niveaus | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – | j | – – | J | Rijtotaal | ||
| Factor 1 Niveaus | 1 | O11 | – – | O1j | – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – | Oij | – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OI1 | – – | OIj | – – | OIJ | RI | |
| Kolom Totaal | C1 | – – | Cj | – – | CJ | n | |
Tabel 11.4 Vereenvoudigde Algemene Contingentietabel
| Factor 2 Niveaus | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – | j | – – | J | Rijtotaal | ||
| Factor 1 Niveaus | 1 | O | – – | O | – – | O | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | O | – – | O | – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | O | – – | O | – – | O | R | |
| Kolom Totaal | C | – – | C | – – | C | n | |
Zoals in het voorbeeld, berekenen we voor elke kerncel in de tabel wat het verwachte aantal waarnemingen E zou zijn als de twee factoren onafhankelijk waren. E wordt berekend voor elke kerncel (elke cel met een O erin) van tabel 11.4 “Vereenvoudigde algemene contingentietabel” volgens de regel die in het voorbeeld is toegepast:
waarbij R het rijentotaal en C het kolomtotaal is dat bij de cel hoort, en n de steekproefgrootte is.
Nadat het verwachte aantal voor elke cel is berekend, wordt tabel 11.4 “Vereenvoudigde algemene onvoorzienbaarheidstabel” bijgewerkt tot tabel 11.5 “Bijgewerkte algemene onvoorzienbaarheidstabel” door de berekende waarde van E in elke kerncel in te voegen.
Tabel 11.5 Bijgewerkte algemene onvoorziene tabel
| Factor 2 Niveaus | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – | j | – – | J | Rijtotaal | ||||
| Factor 1 Niveaus | 1 | OE | – – | OE | – – | OE | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| i | OE | – – | OE | – – | OE | R | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||||
| I | OE | OE | – – | OE | – – | OE | R | ||
| Kolom Totaal | C | – – | C | – – | C | – – | C | n | |
Hier volgt de teststatistiek voor de algemene hypothese op basis van tabel 11.5 “Bijgewerkte algemene contingentietabel”, samen met de voorwaarden dat deze een chi-kwadraatverdeling volgt.
Teststatistiek voor het testen van de onafhankelijkheid van twee factoren
χ2=Σ(O-E)2E
waarbij de som geldt over alle kerncellen van de tabel.
Als
- de twee studiefactoren onafhankelijk zijn, en
- de waargenomen telling O van elke cel in tabel 11.5 “Geactualiseerde algemene contingentietabel” ten minste 5,
bedraagt, dan volgt χ2 bij benadering een chi-kwadraatverdeling met df=(I-1)×(J-1) vrijheidsgraden.
Dezelfde vijfstappenprocedures, hetzij de kritische waardebenadering hetzij de p-waardebenadering, die zijn geïntroduceerd in Paragraaf 8.1 “De elementen van het toetsen van hypothesen” en Paragraaf 8.3 “De waargenomen significantie van een toets” van Hoofdstuk 8 “Hypothesen toetsen”, worden gebruikt om de toets uit te voeren, die altijd een rechtse staart heeft.
Voorbeeld 1
Een onderzoeker wil nagaan of de scores van studenten op een toelatingsexamen voor de universiteit (CEE) enige indicatieve kracht hebben voor toekomstige prestaties op de universiteit, zoals gemeten door het GPA. Met andere woorden, hij wil nagaan of de factoren CEE en GPA onafhankelijk zijn of niet. Hij selecteert willekeurig n = 100 studenten in een college en noteert van elke student de score op het toelatingsexamen en zijn grade point average aan het eind van het tweede jaar. Hij verdeelt de toelatingsexamenscores in twee niveaus en de puntengemiddelden in drie niveaus. Door de gegevens volgens deze verdelingen te sorteren, vormt hij de contingentietabel in tabel 11.6 “Contingentietabel CEE versus GPA”, waarin de totalen van de rijen en kolommen reeds zijn berekend.
Tabel 11.6 CEE versus GPA Contingentietabel
| GPA | |||||
|---|---|---|---|---|---|
| 2,7 | 2,7 tot 3,2 | >3.2 | Rijtotaal | ||
| CEE | 1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Kolom Totaal | 41 | 36 | 23 | Totaal=100 | |
Test, op het 1%-niveau van significantie, of deze gegevens voldoende bewijs leveren om te concluderen dat CEE-scores een aanwijzing zijn voor toekomstige prestatieniveaus van binnenkomende eerstejaarsstudenten zoals gemeten door GPA.
Oplossing:
We voeren de test uit met behulp van de kritische-waardebenadering, volgens de gebruikelijke vijfstappenmethode die wordt beschreven aan het eind van Paragraaf 8.1 “De elementen van het testen van hypothesen” in hoofdstuk 8 “Hypothesen testen”.
-
Stap 1. De hypothesen zijn
H0:CEE en GPA zijn onafhankelijke factorenvs. Ha:CEE en GPA zijn geen onafhankelijke factoren
- Step 2. De verdeling is chi-kwadraat.
-
Step 3. Om de waarde van de teststatistiek te berekenen moeten we eerst het verwachte aantal berekenen voor elk van de zes kerncellen (die waarvan de gegevens vetgedrukt zijn):
- 1e rij en 1e kolom: E=(R×C)∕n=41×52∕100=21,32
- 1e rij en 2e kolom: E=(R×C)∕n=36×52∕100=18,72
- 1e rij en 3e kolom: E=(R×C)∕n=23×52∕100=11,96
- 2e rij en 1e kolom: E=(R×C)∕n=41×48∕100=19,68
- 2e rij en 2e kolom: E=(R×C)∕n=36×48∕100=17,28
- 2e rij en 3e kolom: E=(R×C)∕n=23×48∕100=11.04
Tabel 11.6 “CEE versus GPA Contingentietabel” wordt bijgewerkt tot tabel 11.7 “Bijgewerkte CEE versus GPA Contingentietabel”.
Tabel 11.7 Bijgewerkte CEE versus GPA Contingentietabel
GPA <2.7 2.7 tot 3.2 >3.2 Rijtotaal CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Kolom Totaal C = 41 C = 36 C = 23 n = 100 De test statistiek is
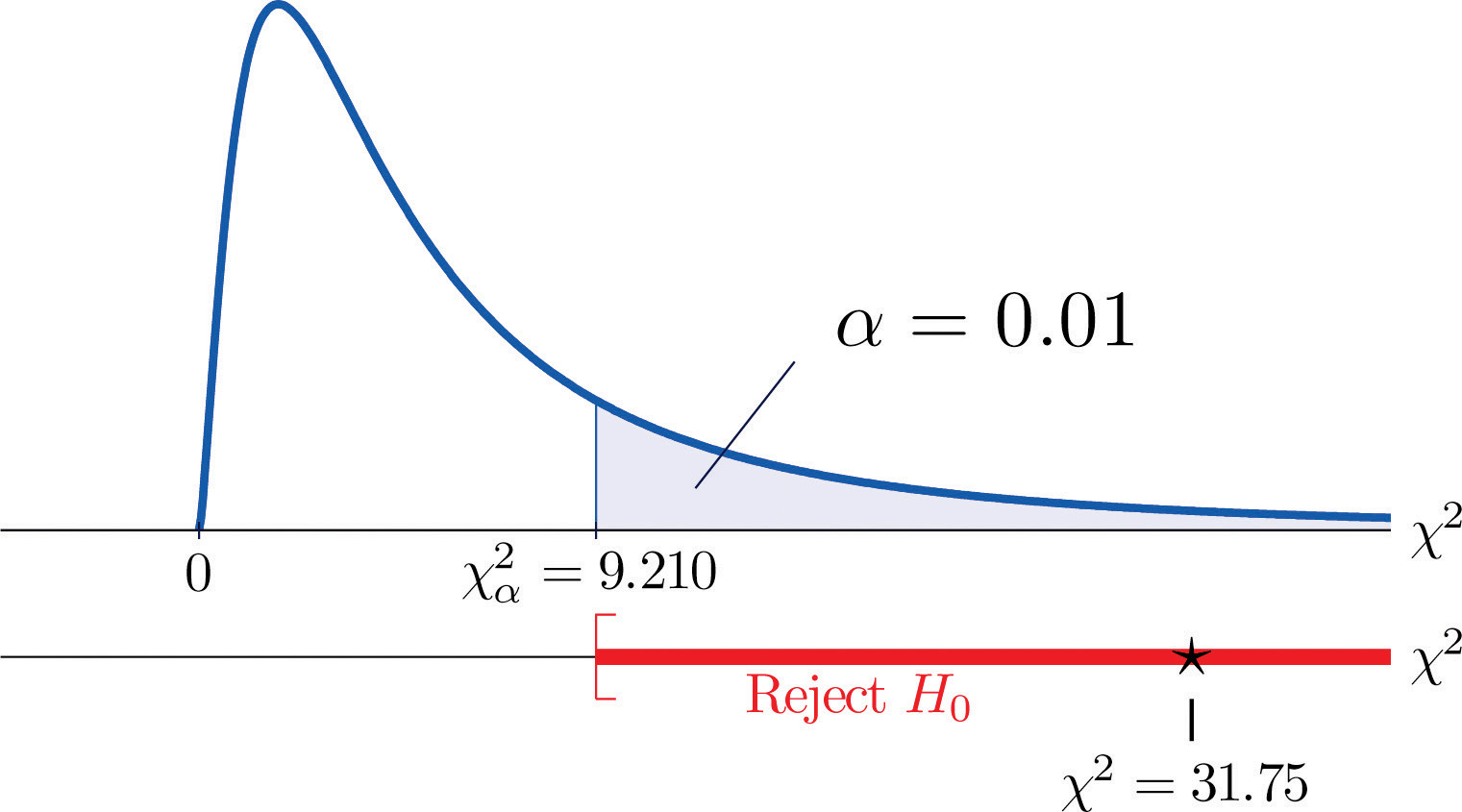
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Aangezien de CEE-factor twee niveaus heeft en de GPA-factor drie, I = 2 en J = 3. De teststatistiek volgt dus de chi-kwadraatverdeling met df=(2-1)×(3-1)=2 vrijheidsgraden.
Omdat de test een rechtse staart heeft, is de kritische waarde χ0,012. Afgelezen uit figuur 12.4 “Kritische waarden van Chi-kwadraatverdelingen”, is χ0.012=9.210, dus het afwijzingsgebied is [9.210,∞).
- Stap 5. Aangezien 31,75 > 9,21 wordt besloten de nulhypothese te verwerpen. Zie figuur 11.4. De gegevens leveren voldoende bewijs, op het 1%-niveau van significantie, om te concluderen dat CEE-score en GPA niet onafhankelijk zijn: de toelatingsexamenscore heeft voorspellende kracht.
Figuur 11.4 Opmerking 11.9 “Voorbeeld 1”
Key Takeaways
- Kritische waarden van een chi-kwadraatverdeling met vrijheidsgraden df zijn te vinden in figuur 12.4 “Kritische waarden van Chi-kwadraatverdelingen”.
- Een chi-kwadraattoetsEen toets op basis van een chi-kwadraatstatistiek om na te gaan of twee factoren onafhankelijk zijn. kan worden gebruikt om de hypothese te evalueren dat twee willekeurige variabelen of factoren onafhankelijk zijn.
Oefeningen
-
Vind χ0.012 voor elk van de volgende aantal vrijheidsgraden.
- df=5
- df=11
- df=25
-
Vind χ0.052 voor elk van het volgende aantal vrijheidsgraden.
- df=6
- df=12
- df=30
-
Vind χ0.102 voor elk van het volgende aantal vrijheidsgraden.
- df=6
- df=12
- df=30
-
Vind χ0.012 voor elk van de volgende aantal vrijheidsgraden.
- df=7
- df=10
- df=20
-
Voor df=7 en α=0.05, vind
- χα2
- χα22
-
Voor df=17 en α=0.01, vind
- χα2
- χα22
-
Een gegevensmonster is gesorteerd in een 2 × 2 contingentietabel op basis van twee factoren, die elk twee niveaus hebben.
Factor 1 Level 1 Level 2 Rijtotaal Factor 2 Level 1 20 10 R Level 2 15 5 R Kolomtotaal C C n - Vind de kolomtotalen, de rijtotalen, en het eindtotaal, n, van de tabel.
- Vind het verwachte aantal waarnemingen E voor elke cel op basis van de veronderstelling dat de twee factoren onafhankelijk zijn (dat wil zeggen, gebruik gewoon de formule E=(R×C)∕n).
- Vind de waarde van de chi-kwadraat-teststatistiek χ2.
- Vind het aantal vrijheidsgraden van de chi-kwadraat-teststatistiek.
-
Een gegevensmonster wordt gesorteerd in een 3 × 2 contingentietabel op basis van twee factoren, waarvan de ene drie niveaus en de andere twee niveaus heeft.
Factor 1 Level 1 Level 2 Rijtotaal Factor 2 Level 1 20 10 R Level 2 15 5 R Level 3 10 20 R Kolomtotaal C C n - Vind de kolomtotalen, de rijtotalen, en het eindtotaal, n, van de tabel.
- Vind het verwachte aantal waarnemingen E voor elke cel op basis van de veronderstelling dat de twee factoren onafhankelijk zijn (dat wil zeggen, gebruik gewoon de formule E=(R×C)∕n).
- Vind de waarde van de chi-kwadraat-teststatistiek χ2.
- Vind het aantal vrijheidsgraden van de chi-kwadraat-teststatistiek.
Basic
-
Een kinderpsycholoog gelooft dat kinderen beter presteren op toetsen als ze een waargenomen keuzevrijheid krijgen. Om deze overtuiging te testen, voerde de psycholoog een experiment uit waarbij 200 derde klassers willekeurig werden ingedeeld in twee groepen, A en B. Elk kind kreeg dezelfde eenvoudige logische test. In groep B echter kreeg elk kind de vrijheid om een tekstboekje te kiezen uit vele met verschillende tekeningen op de omslagen. De prestaties van elk kind werden beoordeeld als zeer goed, goed en redelijk. De resultaten zijn in de tabel samengevat. Test, op het 5% niveau van significantie, of er voldoende bewijs is in de gegevens om de overtuiging van de psycholoog te ondersteunen.
Groep A B Prestatie Zeer goed 32 29 Goed 55 61 eerlijk 10 13 Met betrekking tot wedstrijden wijnproeven, beweren veel deskundigen dat het eerste glas wijn dat wordt geserveerd een referentiesmaak bepaalt en dat een andere referentiewijn de relatieve rangorde van de andere wijnen in de competitie kan veranderen. Om deze bewering te testen, werden drie wijnen, A, B en C, geserveerd tijdens een wijnproeverij. Elke persoon kreeg één glas van elke wijn geserveerd, maar in verschillende volgorde voor verschillende gasten. Aan het eind werd iedereen gevraagd de beste van de drie te noemen. Honderdtweeënzeventig mensen waren op het evenement aanwezig en hun topkeuzes staan in de bijgevoegde tabel. Test, op het niveau van 1% significantie, of er voldoende bewijs is in de gegevens om de bewering te staven dat de voorkeur van de wijnkenners afhangt van de eerst geserveerde wijn.
Top Pick A B C Eerste glas A 12 31 27 B 15 40 21 C 10 9 7 Is linkshandig zijnerfelijk? Om deze vraag te beantwoorden worden 250 volwassenen willekeurig geselecteerd en wordt hun handigheid en die van hun ouders genoteerd. De resultaten zijn samengevat in de tabel. Test, op het 1%-niveau van significantie, of er voldoende bewijs is in de gegevens om te concluderen dat er een erfelijk element is in handvaardigheid.
Aantal ouders links-Handig 0 1 2 Handigheid Links 8 10 12 Rechts 178 21 21 Sommige genetici beweren dat de genen die linkshandigheid bepalenook de ontwikkeling van de taalcentra in de hersenen bepalen. Als deze bewering waar is, dan zou redelijkerwijs te verwachten zijn dat linkshandigen over het algemeen sterkere taalvaardigheden hebben. In een studie om deze bewering te toetsen werden willekeurig 807 studenten geselecteerd die het Graduate Record Examination (GRE) aflegden. Hun scores op het taalgedeelte van het examen werden ingedeeld in drie categorieën: laag, gemiddeld en hoog, en ook hun handigheid werd genoteerd. De resultaten staan in de tabel. Test, op het niveau van 5% significantie, of er voldoende bewijs is in de gegevens om te concluderen dat linkshandigen de neiging hebben om sterkere taalvaardigheden te hebben.
GRE English Scores Low Average Hoog Handigheid Links 18 40 22 Rechts 201 360 166 In het algemeen wordt aangenomen dat kinderen die in stabiele gezinnen worden opgevoed, het meestal goed doen op school. Om deze overtuiging te staven, onderzocht een sociale wetenschapper de gegevens van 290 willekeurig geselecteerde leerlingen van een openbare middelbare school en noteerde van elke leerling de gezinsstructuur en de academische status vier jaar na het begin van de middelbare schooltijd. De gegevens werden vervolgens gesorteerd in een 2 × 3 contingentietabel met twee factoren. Factor 1 heeft twee niveaus: afgestudeerd en niet afgestudeerd. Factor 2 heeft drie niveaus: geen ouder, één ouder, en twee ouders. De resultaten staan in de tabel. Test, op het niveau van 1% significantie, of er voldoende bewijs in de gegevens is om te concluderen dat de gezinsstructuur van belang is voor de schoolprestaties van de leerlingen.
Academic Status Graduated Did Not Graduate Familie Geen ouder 18 31 Een ouder 101 44 twee ouders 70 26 Een grote bestuurder van een middelbare school wil zijn invloed als beroemdheid aanwenden om leerlingen te stimuleren gezondere keuzes te maken in de schoolkantine. De cafetaria bevindt zich in het midden van een open ruimte. Elke dag rond lunchtijd krijgen de leerlingen hun lunch en een drankje in drie aparte rijen die naar drie aparte stations leiden. Bij wijze van experiment heeft de schooldirecteur een poster opgehangen van een populaire tienerpopster die melk drinkt op elk van de drie plaatsen waar drankjes worden verstrekt, behalve dat de melk op de poster op elke plaats anders is: op de ene staat witte melk, op de andere roze melk met aardbeiensmaak, en op de derde chocolademelk. Na de eerste dag van het experiment noteerde de beheerder de melkkeuzes van de leerlingen afzonderlijk voor de drie lijnen. De gegevens staan in de tabel. Test, op het niveau van 1% significantie, of er voldoende bewijs is in de gegevens om te concluderen dat de posters enige invloed hadden op de drankkeuzes van de leerlingen.
Student Choice Regular Strawberry Chocolate Poster Choice Regular 38 28 40 Strawberry 18 51 24 Chocolade 32 32 53 -
Large In dataset 8 is het resultaat opgenomen van een enquête onder 300 willekeurig gekozen volwassenen die regelmatig naar de bioscoop gaan. Van elke persoon werden het geslacht en het type film van voorkeur genoteerd. Test, op het niveau van 5% significantie, of de gegevens voldoende bewijs leveren om te concluderen dat de factoren “geslacht” en “voorkeurstype film” afhankelijk zijn.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Groot Dataset Oefening
Antwoorden
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5.99, niet afwijzen H0
-
χ2=72.35, χ0.012=9.21, niet afwijzen H0
-
χ2=21.2784, χ0.012=9.21, verwerp H0
-
χ2=28.4539. df=3. Afwijzingsgebied: [7.815,∞). Besluit: Verwerp H0 van onafhankelijkheid.