Testy na niezależność
Testy hipotez spotykane we wcześniejszej części książki dotyczyły tego, jak porównywane są wartości liczbowe dwóch parametrów populacji. W tym podrozdziale będziemy badać hipotezy, które mają związek z tym, czy dwie zmienne losowe przyjmują swoje wartości niezależnie, czy też wartość jednej z nich ma związek z wartością drugiej. Hipotezy będą więc wyrażone słowami, a nie symbolami matematycznymi. Dyskusja toczy się wokół następującego przykładu.
Istnieje teoria, że płeć dziecka w łonie matki jest związana z jego tętnem: dziewczynki mają wyższe tętno. Załóżmy, że chcemy sprawdzić tę teorię. Badamy zapisy tętna 40 niemowląt pobrane podczas ostatnich badań prenatalnych ich matek przed porodem i dla każdego z tych 40 losowo wybranych zapisów obliczamy wartości dwóch miar losowych: 1) płci i 2) częstości akcji serca. W tym kontekście te dwie miary losowe są często nazywane czynnikamiZmienna o kilku poziomach jakościowych. Ponieważ ciężar dowodu spoczywa na tym, że częstość akcji serca i płeć są powiązane, a nie że nie są powiązane, problem testowania teorii dotyczącej płci dziecka i częstości akcji serca można sformułować jako test następujących hipotez:
H0:Płeć dziecka i częstość akcji serca dziecka są niezależnevs. Ha:płeć dziecka i częstość akcji serca dziecka nie są niezależne
Czynnik płeć ma dwie naturalne kategorie lub poziomy: chłopiec i dziewczynka. Dzielimy drugi czynnik, częstość akcji serca, na dwa poziomy, niski i wysoki, wybierając pewną częstość akcji serca, powiedzmy 145 uderzeń na minutę, jako granicę między nimi. Tętno poniżej 145 uderzeń na minutę będzie uważane za niskie, a 145 i więcej za wysokie. 40 rekordów daje podstawę do utworzenia tabeli kontyngencji 2 × 2. Przypisując sumy wierszy, sumy kolumn i sumę całkowitą otrzymujemy tabelę przedstawioną jako Tabela 11.1 „Płeć dziecka a częstość akcji serca”. Cztery wpisy wyróżnione pogrubioną czcionką są liczbą obserwacji z próby n = 40. Było 11 dziewczynek z niskim tętnem, 17 chłopców z niskim tętnem, i tak dalej. Stanowią one rdzeń rozszerzonej tabeli.
Tabela 11.1 Płeć dziecka a częstość akcji serca
| Częstość akcji serca | ||||
|---|---|---|---|---|
| Niska | Wysoka | Row Total | ||
| Gender | Girl | 11 | 7 | 18 |
| Chłopiec | 17 | 5 | 22 | |
| Column Total | 28 | 12 | Total = 40 | |
W analogii do faktu, że prawdopodobieństwo zdarzeń niezależnych jest iloczynem prawdopodobieństw każdego zdarzenia, jeśli częstość akcji serca i płeć byłyby niezależne, wówczas oczekiwalibyśmy, że liczba w każdej komórce rdzenia będzie bliska iloczynowi sumy wierszy R i sumy kolumn C wiersza i kolumny zawierającej tę komórkę, podzielonemu przez wielkość próby n. Oznaczając taką oczekiwaną liczbę obserwacji E, te cztery oczekiwane wartości to:
- 1. wiersz i 1. kolumna: E=(R×C)∕n=18×28∕40=12,6
- 1. wiersz i 2. kolumna: E=(R×C)∕n=18×12∕40=5,4
- 2. wiersz i 1. kolumna: E=(R×C)∕n=22×28∕40=15,4
- 2. wiersz i 2. kolumna: E=(R×C)∕n=22×12∕40=6,6
Uaktualniamy tabelę 11.1 „Płeć dziecka a częstość akcji serca”, umieszczając każdą wartość oczekiwaną w odpowiadającej jej komórce głównej, tuż pod wartością obserwowaną w tej komórce. W ten sposób otrzymujemy zaktualizowaną tabelę Tabela 11.2 „Zaktualizowana płeć dziecka i częstość akcji serca”.
Tabela 11.2 Updated Baby Gender and Heart Rate
| Heart Rate | ||||
|---|---|---|---|---|
| Low | High | Row Total | ||
| Gender | Girl | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Chłopiec | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Column Total | C = 28 | C = 12 | n = 40 | |
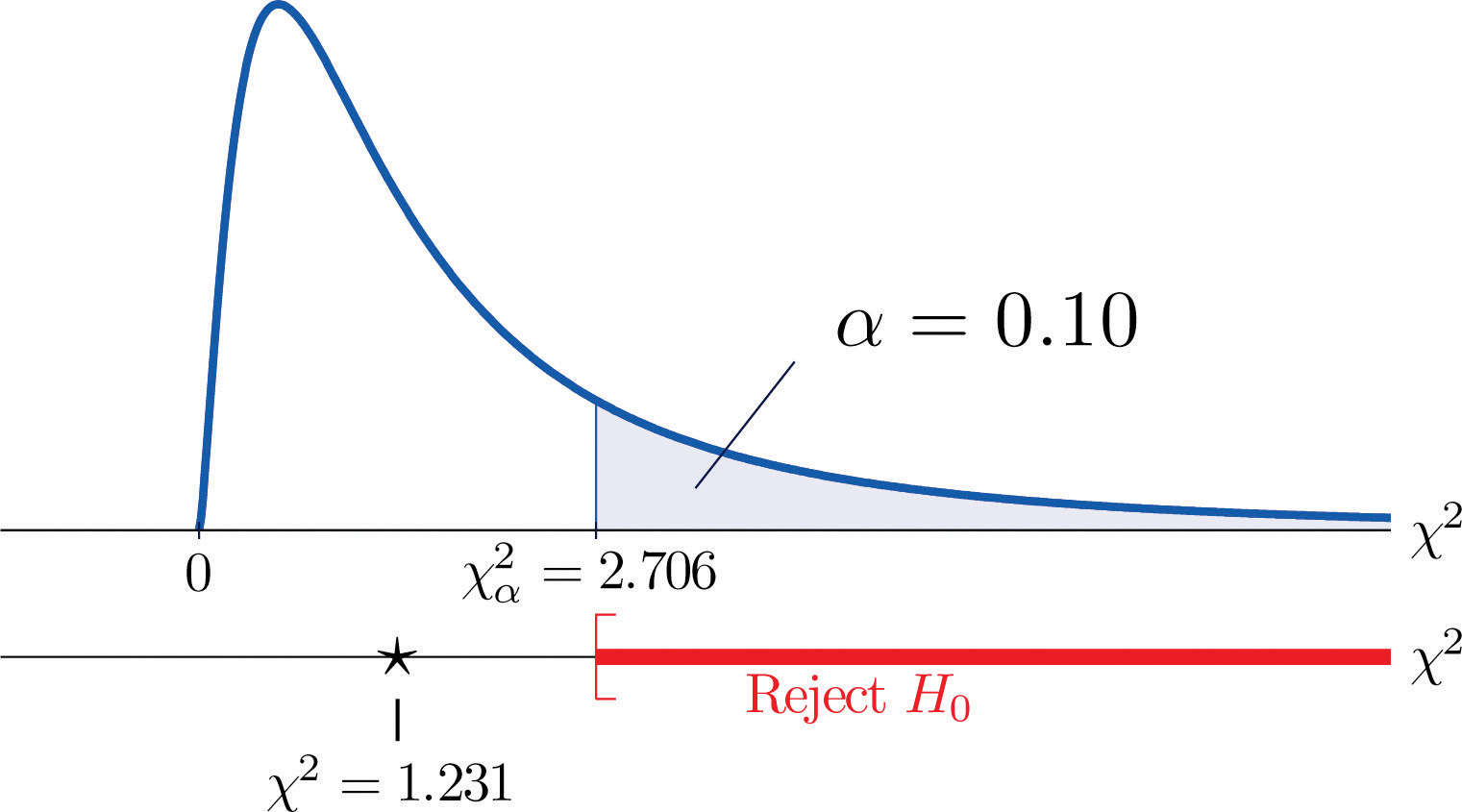
Miarą tego, jak bardzo dane odbiegają od tego, co spodziewalibyśmy się zobaczyć, gdyby czynniki naprawdę były niezależne, jest suma kwadratów różnicy liczb w każdej komórce rdzenia, lub, standaryzując poprzez podzielenie każdego kwadratu przez oczekiwaną liczbę w komórce, suma Σ(O-E)2∕E. Odrzucilibyśmy hipotezę zerową, że czynniki są niezależne tylko wtedy, gdyby ta liczba była duża, więc test jest prawoskrętny. W tym przykładzie zmienna losowa Σ(O-E)2∕E ma rozkład chi kwadrat z jednym stopniem swobody. Jeśli zdecydowalibyśmy się na początku na testowanie na 10% poziomie istotności, wartość krytyczna definiująca region odrzucenia byłaby, czytając z Rysunku 12.4 „Wartości krytyczne rozkładów Chi-kwadrat”, χα2=χ0.102=2.706, tak więc region odrzucenia byłby przedziałem [2.706,∞). Po obliczeniu wartości standaryzowanej statystyki testowej otrzymujemy
Σ(O-E)2E=(11-12,6)212,6+(7-5,4)25,4+(17-15,4)215,4+(5-6,6)26,6=1,231
Ponieważ 1,231 < 2,706, decyzją jest nieodrzucenie H0. Zobacz Rysunek 11.3 „Przewidywanie płci dziecka”. Dane nie dostarczają wystarczających dowodów, na 10% poziomie istotności, aby stwierdzić, że częstość akcji serca i płeć są powiązane.
Rysunek 11.3 „Baby Gender Prediction”
Mając na uwadze ten konkretny przykład, przejdźmy teraz do sytuacji ogólnej. W ogólnym przypadku testowania niezależności dwóch czynników, nazywanych czynnikiem 1 i czynnikiem 2, hipotezy do przetestowania to
H0:Dwa czynniki są niezależnevs. Ha:Dwa czynniki nie są niezależne
Jak w przykładzie, każdy czynnik jest podzielony na pewną liczbę kategorii lub poziomów. Mogą one powstać naturalnie, jak w przypadku podziału płci na chłopięcą i dziewczęcą, lub nieco arbitralnie, jak w przypadku podziału częstości akcji serca na wysoką i niską. Załóżmy, że czynnik 1 ma I poziom, a czynnik 2 ma J poziom. Wtedy informacje z próby losowej dają podstawę do stworzenia ogólnej tabeli kontyngencji I × J, która z sumami wierszy, sumami kolumn i sumą całkowitą wyglądałaby tak, jak pokazano w Tabeli 11.3 „Ogólna tabela kontyngencji”. Każda komórka może być oznaczona parą indeksów (i,j). Oij oznacza liczbę obserwacji w komórce w wierszu i i kolumnie j, Ri – sumę i-tego wiersza, a Cj – sumę j-tej kolumny. Aby uprościć zapis, zrezygnujemy z indeksów, więc tabela 11.3 „Ogólna tabela kontyngencji” staje się tabelą 11.4 „Uproszczona ogólna tabela kontyngencji”. Niemniej jednak ważne jest, aby pamiętać, że Os, R i C, choć oznaczone tymi samymi symbolami, są w rzeczywistości różnymi liczbami.
Tabela 11.3 Ogólna Tabela Wariantów
| Poziomy czynnika 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – – | j | – – – | J | Row Total | ||
| Poziomy czynnika 1 | 1 | O11 | – – – | O1j | – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – | Oij | – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OI1 | – – – – | OIj | – – – | OIJ | RI | |
| Suma kolumn | C1 | – – – – | Cj | – – – | CJ | n | |
Tabela 11.4 Uproszczona Ogólna Tabela Wariantów
| Poziomy czynnika 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Row Total | ||
| Poziomy czynnika 1 | 1 | O | – – – | O | – – – | O | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – | O | – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | O | O | – – – – | O | – – – | O | R |
| Suma kolumn | C | – – – | C | – – – | C | n | |
Jak w przykładzie, dla każdej komórki rdzenia w tabeli obliczamy, jaka byłaby oczekiwana liczba E obserwacji, gdyby te dwa czynniki były niezależne. E jest obliczane dla każdej komórki głównej (każdej komórki z literą O) tabeli 11.4 „Uproszczona ogólna tabela kontyngencji” według zasady zastosowanej w przykładzie:
gdzie R jest sumą wierszy i C jest sumą kolumn odpowiadających komórce, a n jest liczebnością próby.
Po obliczeniu oczekiwanej liczby dla każdej komórki, tabela 11.4 „Uproszczona ogólna tabela kontyngencji” jest aktualizowana do postaci tabeli 11.5 „Zaktualizowana ogólna tabela kontyngencji” poprzez wstawienie obliczonej wartości E do każdej komórki rdzenia.
Tabela 11.5 Updated General Contingency Table
| Factor 2 Levels | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Row Total | ||
| Poziomy czynnika 1 | 1 | OE | – – – | OE | – – – | OE | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | OE | – – – | OE | – – – | OE | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| I | OE | – – – | OE | – – – – | OE | R | |
| Column Total | C | – – – | C | -. – – | C | n | |
Tutaj znajduje się statystyka testowa dla hipotezy ogólnej na podstawie tabeli 11.5 „Updated General Contingency Table”, wraz z warunkami, że jest ona zgodna z rozkładem chi-kwadrat.
Test Statistic for Testing the Independence of Two Factors
χ2=Σ(O-E)2E
gdzie suma jest nad wszystkimi podstawowymi komórkami tabeli.
Jeśli
- dwa badane czynniki są niezależne, a
- liczba obserwowanych O w każdej komórce w tabeli 11.5 „Zaktualizowana ogólna tabela kontyngencji” wynosi co najmniej 5,
to χ2 w przybliżeniu ma rozkład chi kwadrat z df=(I-1)×(J-1) stopniami swobody.
Te same pięciostopniowe procedury, albo podejście wartości krytycznej, albo podejście wartości p, które zostały wprowadzone w Sekcji 8.1 „Elementy testowania hipotez” i Sekcji 8.3 „Obserwowana istotność testu” w Rozdziale 8 „Testowanie hipotez” są używane do wykonania testu, który jest zawsze prawoskrętny.
Przykład 1
Badacz chce zbadać, czy wyniki studentów na egzaminie wstępnym do college’u (CEE) mają jakąkolwiek moc orientacyjną dla przyszłych wyników w college’u mierzonych GPA. Innymi słowy, chce zbadać, czy czynniki CEE i GPA są niezależne, czy nie. Wybiera losowo n = 100 studentów w college’u i odnotowuje wynik każdego z nich na egzaminie wstępnym oraz ich średnią ocen na koniec drugiego roku studiów. Wyniki egzaminu wstępnego dzieli na dwa poziomy, a średnią ocen na trzy poziomy. Sortując dane zgodnie z tymi podziałami, tworzy tabelę kontyngencji pokazaną jako Tabela 11.6 „CEE versus GPA Contingency Table”, w której sumy wierszy i kolumn zostały już obliczone.
Table 11.6 CEE versus GPA Contingency Table
| GPA | |||||
|---|---|---|---|---|---|
| <2.7 | 2.7 do 3.2 | >3.2 | Row Total | ||
| CEE | <1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Column Total | 41 | 36 | 23 | Total=100 | |
Test, na poziomie istotności 1%, czy te dane dostarczają wystarczających dowodów, aby stwierdzić, że wyniki CEE wskazują przyszły poziom wydajności świeżo przyjętych studentów mierzony GPA.
Rozwiązanie:
Wykonujemy test używając podejścia wartości krytycznej, postępując zgodnie ze zwykłą pięcioetapową metodą przedstawioną na końcu sekcji 8.1 „Elementy testowania hipotez” w rozdziale 8 „Testowanie hipotez”.
-
Krok 1. Hipotezy są następujące
H0:CEE i GPA są czynnikami niezależnymivs. Ha:CEE i GPA nie są czynnikami niezależnymi
- Krok 2. Rozkład jest chi kwadrat.
-
Krok 3. Aby obliczyć wartość statystyki testowej, musimy najpierw obliczyć liczbę oczekiwaną dla każdej z sześciu komórek rdzenia (tych, których wpisy są pogrubione):
- 1. wiersz i 1. kolumna: E=(R×C)∕n=41×52∕100=21,32
- 1. wiersz i 2. kolumna: E=(R×C)∕n=36×52∕100=18,72
- 1. wiersz i 3. kolumna: E=(R×C)∕n=23×52∕100=11,96
- 2. wiersz i 1. kolumna: E=(R×C)∕n=41×48∕100=19,68
- 2. wiersz i 2. kolumna: E=(R×C)∕n=36×48∕100=17,28
- 2. wiersz i 3. kolumna: E=(R×C)∕n=23×48∕100=11,04
Tabela 11.6 „CEE versus GPA Contingency Table” została zaktualizowana do Tabeli 11.7 „Updated CEE versus GPA Contingency Table”.
Tabela 11.7 Updated CEE versus GPA Contingency Table
GPA <2.7 2.7 do 3.2 >3.2 Row Total CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Column Total C = 41 C = 36 C = 23 n = 100 Statystyka testowa wynosi
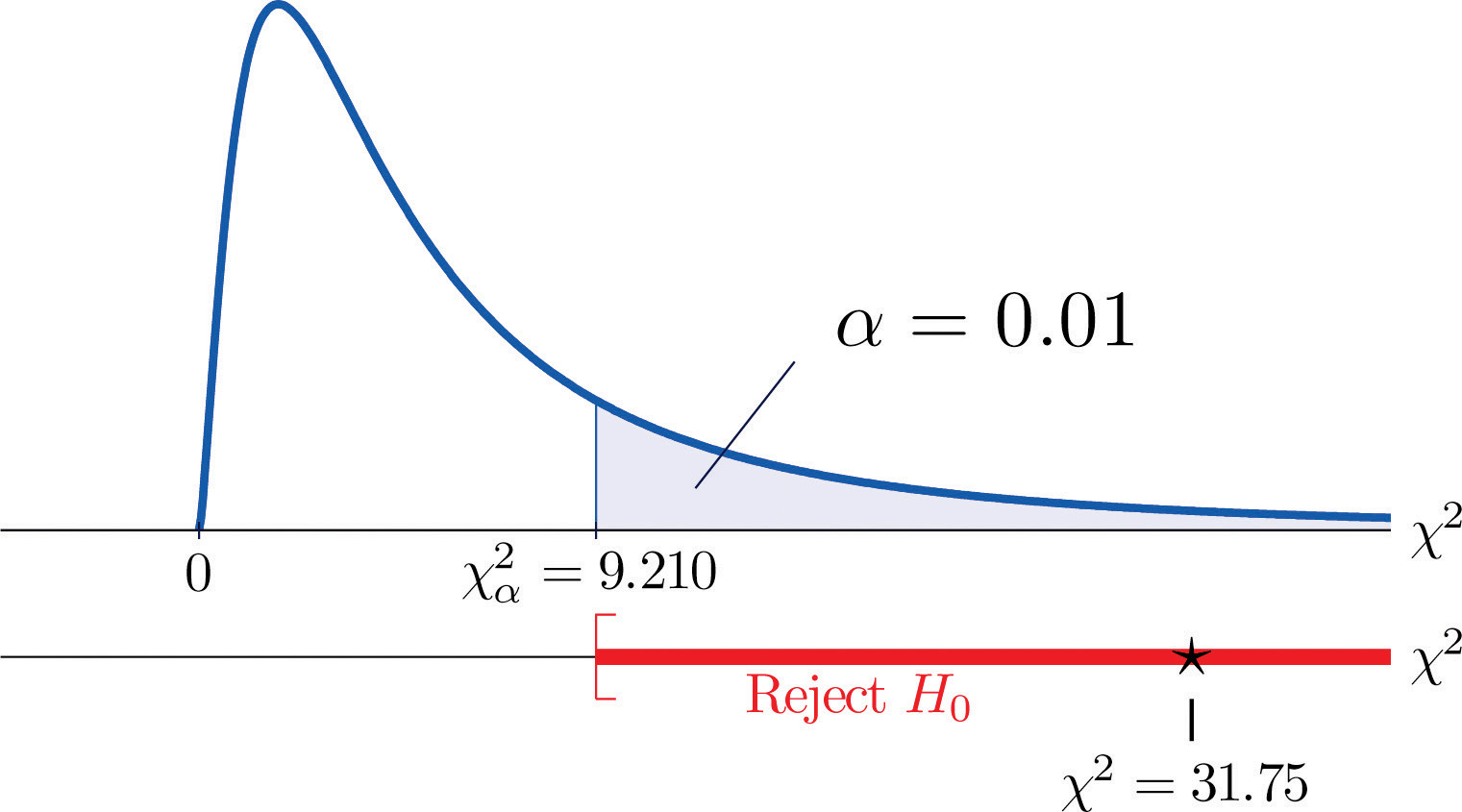
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Ponieważ czynnik CEE ma dwa poziomy, a czynnik GPA ma trzy, I = 2 i J = 3. Zatem statystyka testu ma rozkład chi kwadrat z df=(2-1)×(3-1)=2 stopnie swobody.
Ponieważ test jest prawoskośny, wartość krytyczna wynosi χ0,012. Odczytując z rysunku 12.4 „Wartości krytyczne rozkładów Chi-kwadrat”, χ0,012=9,210, więc region odrzucenia to [9,210,∞).
- Krok 5. Ponieważ 31,75 > 9,21 decyzją jest odrzucenie hipotezy zerowej. Patrz Rysunek 11.4. Dane dostarczają wystarczających dowodów, na poziomie istotności 1%, aby stwierdzić, że wynik CEE i GPA nie są niezależne: wynik egzaminu wstępnego ma moc predykcyjną.
Rysunek 11.4 Uwaga 11.9 „Przykład 1”
Key Takeaways
- Wartości krytyczne rozkładu chi kwadrat o stopniach swobody df znajdują się na rysunku 12.4 „Critical Values of Chi-Square Distributions”.
- Test chi-squareTest oparty na statystyce chi-square sprawdzający, czy dwa czynniki są niezależne. może być użyty do oceny hipotezy, że dwie zmienne losowe lub czynniki są niezależne.
Ćwiczenia
-
Znajdź χ0,012 dla każdej z poniższych liczb stopni swobody.
- df=5
- df=11
- df=25
-
Znajdź χ0.052 dla każdej z następujących liczb stopni swobody.
- df=6
- df=12
- df=30
-
Znajdź χ0.102 dla każdej z następujących liczb stopni swobody.
- df=6
- df=12
- df=30
-
Znajdź χ0.012 dla każdej z następujących liczb stopni swobody.
- df=7
- df=10
- df=20
-
Dla df=7 i α=0.05, find
- χα2
- χα22
-
For df=17 and α=0.01, find
- χα2
- χα22
-
A data sample is sorted into a 2 × 2 contingency table based on two factors, each of which has two levels.
Faktor 1 Poziom 1 .
Level 2 Row Total Factor 2 Level 1 20 10 R Level 2 15 5 R . Całkowita suma kolumn C n - Znajdź sumy kolumn, sumy wierszy i sumę całkowitą, n, tabeli.
- Znajdź oczekiwaną liczbę E obserwacji dla każdej komórki na podstawie założenia, że dwa czynniki są niezależne (czyli po prostu skorzystaj ze wzoru E=(R×C)∕n).
- Znajdź wartość statystyki testu chi kwadrat χ2.
- Znajdź liczbę stopni swobody statystyki testu chi kwadrat.
-
Próba danych jest posortowana do tabeli kontyngencji 3 × 2 na podstawie dwóch czynników, z których jeden ma trzy poziomy, a drugi ma dwa poziomy.
Faktor 1 Poziom 1 Poziom 2 .
Row Total Factor 2 Level 1 20 10 R .
Poziom 2 15 5 R Poziom 3 10 20 R Column Total C C n - Znajdź sumy kolumn, sumy wierszy i sumę całkowitą, n, tabeli.
- Znajdź oczekiwaną liczbę E obserwacji dla każdej komórki na podstawie założenia, że dwa czynniki są niezależne (czyli po prostu skorzystaj ze wzoru E=(R×C)∕n).
- Znajdź wartość statystyki testu chi kwadrat χ2.
- Znajdź liczbę stopni swobody statystyki testu chi kwadrat.
Podstawowe
-
Psycholog dziecięcy uważa, że dzieci osiągają lepsze wyniki w testach, gdy mają postrzeganą swobodę wyboru. Aby sprawdzić to przekonanie, psycholog przeprowadził eksperyment, w którym 200 trzecioklasistów zostało losowo przydzielonych do dwóch grup, A i B. Każde dziecko otrzymało ten sam prosty test logiczny. Jednak w grupie B, każde dziecko otrzymało swobodę wyboru książeczki tekstowej spośród wielu z różnymi rysunkami na okładkach. Wyniki każdego dziecka były oceniane jako bardzo dobre, dobre i dostateczne. Wyniki są podsumowane w podanej tabeli. Przetestuj, na poziomie istotności 5%, czy w danych są wystarczające dowody na poparcie przekonania psychologa.
Grupa A B Performance Very Good 32 29 .
Good 55 61 Fair 10 13 W odniesieniu do konkursów degustacji wina, wielu ekspertów twierdzi, że pierwszy podany kieliszek wina wyznacza smak referencyjny i że inne wino referencyjne może zmienić względny ranking pozostałych win w konkursie. Aby przetestować to twierdzenie, trzy wina, A, B i C, zostały podane na imprezie degustacyjnej. Każdej osobie podano po jednym kieliszku każdego wina, ale w różnej kolejności dla różnych gości. Na zakończenie, każda osoba została poproszona o podanie najlepszego z trzech. Na imprezie były sto siedemdziesiąt dwie osoby, a ich najlepsze wybory są podane w tabeli. Przetestuj, na poziomie istotności 1%, czy istnieją wystarczające dowody w danych, aby poprzeć twierdzenie, że preferencje ekspertów winiarskich zależą od wina podanego jako pierwsze.
Top Pick A B .
C Pierwsza szyba A 12 31 27 B 15 40 21 C 10 9 7 Czy bycie leworęcznym jest dziedziczne?Czy bycie leworęcznym jest dziedziczne? Aby odpowiedzieć na to pytanie, 250 dorosłych osób zostało losowo wybranych i zanotowano ich leworęczność oraz leworęczność ich rodziców. Wyniki są podsumowane w podanej tabeli. Przetestuj, na poziomie istotności 1%, czy istnieją wystarczające dowody w danych, aby stwierdzić, że istnieje element dziedziczności w leworęczności.
Liczba rodziców LeworęcznychHanded 0 1 2 Handedness Left 8 10 12 .
Praworęczność 178 21 21 Niektórzy genetycy twierdzą, że geny, które determinują leworęczność, rządzą również rozwojem języka.regulują również rozwój ośrodków językowych w mózgu. Jeśli to twierdzenie jest prawdziwe, wtedy byłoby rozsądne oczekiwać, że leworęczni ludzie mają tendencję do posiadania silniejszych zdolności językowych. W badaniu zaprojektowanym w celu sprawdzenia tego twierdzenia wybrano losowo 807 studentów, którzy przystąpili do egzaminu Graduate Record Examination (GRE). Ich wyniki w części językowej egzaminu zostały podzielone na trzy kategorie: niskie, średnie i wysokie, a ich leworęczność została również odnotowana. Wyniki są podane w tabeli. Sprawdź, na poziomie istotności 5%, czy istnieją wystarczające dowody w danych, aby stwierdzić, że osoby leworęczne mają większe zdolności językowe.
GRE English Scores Low Average Average .
High Zręczność manualna Left 40 40 22 Prawa 201 360 166 Powszechnie uważa się, że dzieci wychowujące się w stabilnych rodzinach mają tendencję do osiągania dobrych wyników w szkole. Aby zweryfikować takie przekonanie, naukowiec społeczny zbadał 290 losowo wybranych rekordów uczniów w publicznej szkole średniej i odnotował strukturę rodziny każdego ucznia i status akademicki cztery lata po rozpoczęciu nauki w szkole średniej. Dane te zostały następnie posortowane w tabeli kontyngencji 2 × 3 z dwoma czynnikami. Czynnik 1 ma dwa poziomy: ukończył szkołę i nie ukończył szkoły. Czynnik 2 ma trzy poziomy: brak rodzica, jeden rodzic, dwoje rodziców. Wyniki są podane w tabeli. Sprawdź, na poziomie istotności 1%, czy istnieją wystarczające dowody w danych, aby stwierdzić, że struktura rodziny ma znaczenie dla wyników szkolnych uczniów.
Stan naukowy Ukończył szkołę Nie ukończył szkoły Nie ukończył szkoły .
Rodzina Brak rodzica 18 31 Jeden rodzic .
101 44 Dwoje rodziców 70 26 Administrator dużego gimnazjum chce wykorzystać wpływy celebrytów, aby zachęcić uczniów do dokonywania zdrowszych wyborów w szkolnej stołówce. Kafeteria znajduje się w centrum otwartej przestrzeni. Codziennie w porze lunchu uczniowie otrzymują swój lunch i napój w trzech oddzielnych liniach prowadzących do trzech oddzielnych stacji serwujących. W ramach eksperymentu administrator szkoły umieścił plakat popularnej nastoletniej gwiazdy popu pijącej mleko w każdym z trzech miejsc, w których podawane są napoje, z tym że mleko na plakacie jest inne w każdym miejscu: w jednym miejscu pokazane jest mleko białe, w drugim różowe o smaku truskawkowym, a w trzecim mleko czekoladowe. Po pierwszym dniu eksperymentu administrator odnotował wybory uczniów dotyczące mleka osobno dla trzech linii. Dane te są podane w zamieszczonej tabeli. Sprawdź, na poziomie istotności 1%, czy w danych są wystarczające dowody, aby stwierdzić, że plakaty miały jakiś wpływ na wybory uczniów dotyczące napojów.
Wybór studenta Zwykły Truskawkowy Czekoladowy .
Wybór plakatu Regular 38 28 40 Truskawka 18 .
51 24 Czekolada 32 32 53 -
Large W zestawie danych 8 zapisano wyniki ankiety przeprowadzonej wśród 300 losowo wybranych dorosłych osób, które regularnie chodzą do kina. Dla każdej osoby zapisano płeć i preferowany rodzaj filmu. Przetestuj, na poziomie istotności 5%, czy w danych są wystarczające dowody, aby stwierdzić, że czynniki „płeć” i „preferowany rodzaj filmu” są zależne.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Duży Zestaw danych Ćwiczenie
Odpowiedzi
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5,99, nie odrzucić H0
-
χ2=72,35, χ0,012=9,21, odrzucić H0
-
χ2=21.2784, χ0,012=9,21, odrzuć H0
-
χ2=28,4539. df=3. Region odrzuceń: [7.815,∞). Decyzja: Odrzucić H0 o niezależności.
.