Tests für die Unabhängigkeit
Die Hypothesentests, auf die wir früher in diesem Buch gestoßen sind, hatten damit zu tun, wie die numerischen Werte zweier Populationsparameter miteinander verglichen werden. In diesem Unterabschnitt werden wir Hypothesen untersuchen, die damit zu tun haben, ob zwei Zufallsvariablen ihre Werte unabhängig voneinander annehmen oder ob der Wert der einen mit dem Wert der anderen zusammenhängt. Die Hypothesen werden also in Worten und nicht in mathematischen Symbolen ausgedrückt. Die Diskussion wird anhand des folgenden Beispiels geführt:
Es gibt eine Theorie, dass das Geschlecht eines Babys im Mutterleib mit der Herzfrequenz des Babys zusammenhängt: Mädchen haben tendenziell eine höhere Herzfrequenz. Nehmen wir an, wir wollen diese Theorie testen. Wir untersuchen die Herzfrequenzaufzeichnungen von 40 Babys, die bei den letzten vorgeburtlichen Untersuchungen ihrer Mütter vor der Entbindung aufgenommen wurden, und berechnen für jede dieser 40 zufällig ausgewählten Aufzeichnungen die Werte von zwei Zufallsmaßen: 1) Geschlecht und 2) Herzfrequenz. In diesem Zusammenhang werden diese beiden Zufallsmaße oft als Faktoren bezeichnet Eine Variable mit mehreren qualitativen Ebenen… Da die Beweislast darin besteht, dass die Herzfrequenz und das Geschlecht zusammenhängen, und nicht darin, dass sie nicht miteinander verbunden sind, kann das Problem der Überprüfung der Theorie über das Geschlecht und die Herzfrequenz von Babys als Test der folgenden Hypothesen formuliert werden:
H0:Das Geschlecht und die Herzfrequenz von Babys sind unabhängigvs. Ha:Das Geschlecht des Babys und die Herzfrequenz des Babys sind nicht unabhängig
Der Faktor Geschlecht hat zwei natürliche Kategorien oder Stufen: Junge und Mädchen. Wir unterteilen den zweiten Faktor, die Herzfrequenz, in zwei Stufen, niedrig und hoch, indem wir eine bestimmte Herzfrequenz, z. B. 145 Schläge pro Minute, als Grenzwert zwischen beiden wählen. Eine Herzfrequenz unter 145 Schlägen pro Minute wird als niedrig und 145 und mehr als hoch angesehen. Aus den 40 Datensätzen ergibt sich eine 2 × 2 Kontingenztabelle. Durch Aneinanderreihen von Zeilensummen, Spaltensummen und einer Gesamtsumme erhält man die Tabelle 11.1 „Baby Gender and Heart Rate“. Die vier fett gedruckten Einträge sind die Anzahl der Beobachtungen aus der Stichprobe von n = 40. Es gab 11 Mädchen mit niedriger Herzfrequenz, 17 Jungen mit niedriger Herzfrequenz und so weiter. Sie bilden den Kern der erweiterten Tabelle.
Tabelle 11.1 Baby Geschlecht und Herzfrequenz
| Herzfrequenz | ||||
|---|---|---|---|---|
| Niedrig | Hoch | Zeile gesamt | ||
| Geschlecht | Mädchen | 11 | 7 | 18 |
| Junge | 17 | 5 | 22 | |
| Spalte Gesamt | 28 | 12 | Gesamt = 40 | |
In Analogie zu der Tatsache, dass die Wahrscheinlichkeit unabhängiger Ereignisse das Produkt der Wahrscheinlichkeiten der einzelnen Ereignisse ist, Wenn die Herzfrequenz und das Geschlecht unabhängig wären, würden wir erwarten, dass die Anzahl in jeder Kernzelle nahe dem Produkt aus der Zeilensumme R und der Spaltensumme C der Zeile und Spalte, die sie enthält, geteilt durch den Stichprobenumfang n, liegt. Nennen wir eine solche erwartete Anzahl von Beobachtungen E, so lauten diese vier erwarteten Werte:
- 1.Zeile und 1.Spalte: E=(R×C)∕n=18×28∕40=12,6
- 1. Zeile und 2. Spalte: E=(R×C)∕n=18×12∕40=5.4
- 2. Zeile und 1. Spalte: E=(R×C)∕n=22×28∕40=15,4
- 2. Zeile und 2. Spalte: E=(R×C)∕n=22×12∕40=6.6
Wir aktualisieren die Tabelle 11.1 „Geschlecht des Babys und Herzfrequenz“, indem wir jeden erwarteten Wert in die entsprechende Kernzelle setzen, direkt unter den beobachteten Wert in der Zelle. Dies ergibt die aktualisierte Tabelle 11.2 „Aktualisiertes Geschlecht und Herzfrequenz des Babys“.
Tabelle 11.2 Aktualisiertes Geschlecht und Herzfrequenz des Babys
| Herzfrequenz | ||||
|---|---|---|---|---|
| Niedrig | Hoch | Zeile gesamt | ||
| Geschlecht | Mädchen | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Junge | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Spaltengesamt | C = 28 | C = 12 | n = 40 | |
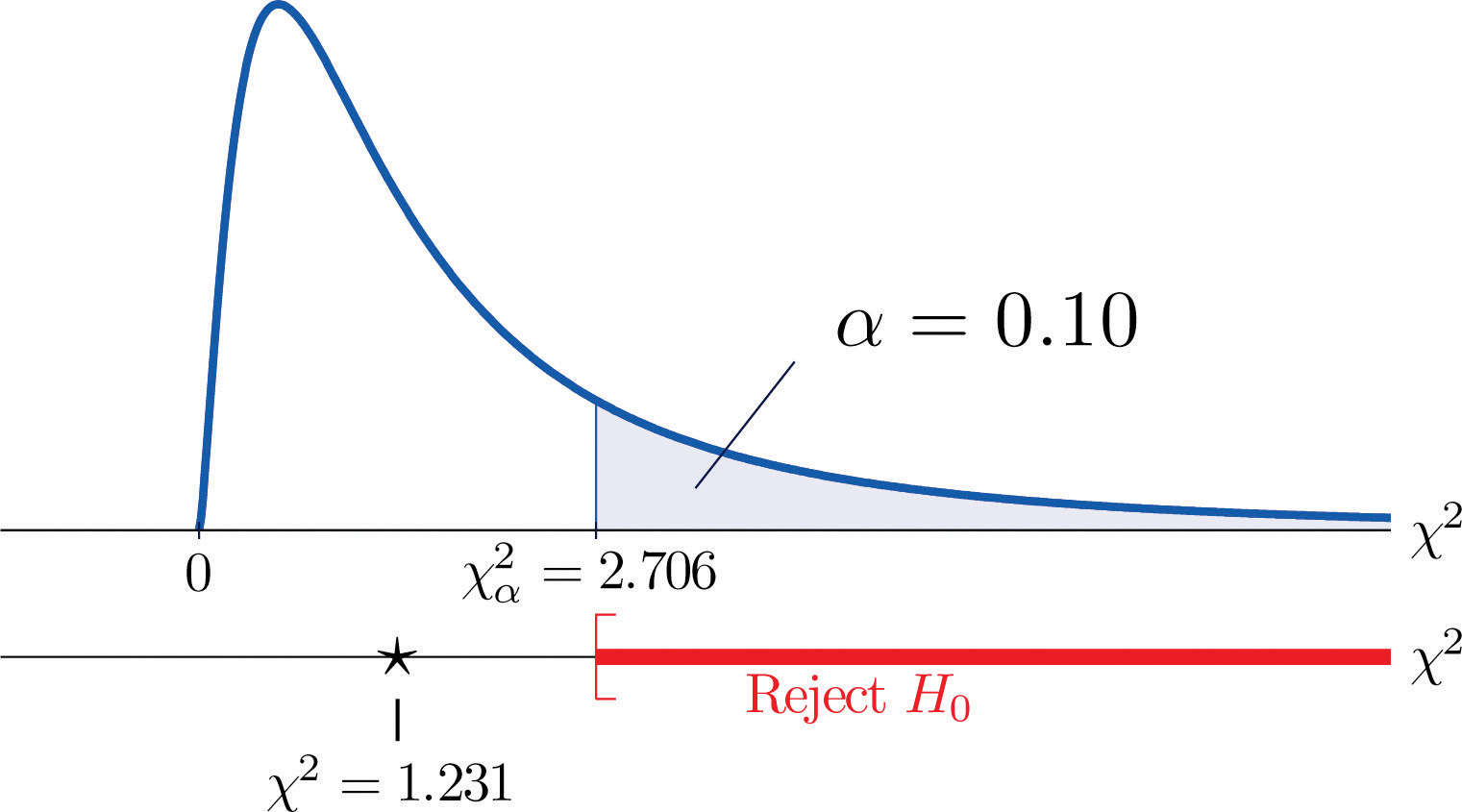
Ein Maß dafür, wie sehr die Daten von dem abweichen, was wir erwarten würden, wenn die Faktoren wirklich unabhängig wären, ist die Summe der Quadrate der Differenz der Zahlen in jeder Kernzelle, oder, standardisiert durch Teilung jedes Quadrats durch die erwartete Anzahl in der Zelle, die Summe Σ(O-E)2∕E. Die Nullhypothese, dass die Faktoren unabhängig sind, würde nur dann abgelehnt, wenn diese Zahl groß ist, der Test ist also rechtsschief. In diesem Beispiel hat die Zufallsvariable Σ(O-E)2∕E die Chi-Quadrat-Verteilung mit einem Freiheitsgrad. Hätten wir zu Beginn beschlossen, auf dem Signifikanzniveau von 10 % zu testen, wäre der kritische Wert, der den Ablehnungsbereich definiert, nach Abbildung 12.4 „Kritische Werte von Chi-Quadrat-Verteilungen“ χα2=χ0,102=2,706, so dass der Ablehnungsbereich das Intervall [2,706,∞) wäre. Wenn wir den Wert der standardisierten Teststatistik berechnen, erhalten wir
Σ(O-E)2E=(11-12.6)212.6+(7-5.4)25.4+(17-15.4)215.4+(5-6.6)26.6=1.231
Da 1.231 < 2.706, lautet die Entscheidung, H0 nicht zu verwerfen. Siehe Abbildung 11.3 „Vorhersage des Geschlechts des Babys“. Die Daten liefern auf dem 10 %-Signifikanzniveau keinen ausreichenden Beweis für die Schlussfolgerung, dass die Herzfrequenz und das Geschlecht zusammenhängen.
Abbildung 11.3 Vorhersage des Geschlechts des Babys
Mit diesem speziellen Beispiel im Hinterkopf wenden wir uns nun der allgemeinen Situation zu. In der allgemeinen Situation der Prüfung der Unabhängigkeit zweier Faktoren, nennen wir sie Faktor 1 und Faktor 2, sind die zu prüfenden Hypothesen
H0:Die beiden Faktoren sind unabhängigvs. Ha:Die beiden Faktoren sind nicht unabhängig
Wie im Beispiel ist jeder Faktor in eine Reihe von Kategorien oder Stufen unterteilt. Diese können natürlich entstehen, wie bei der Unterteilung in Jungen und Mädchen, oder etwas willkürlich, wie bei der Unterteilung in hoch und niedrig bei der Herzfrequenz. Nehmen wir an, Faktor 1 hat I-Stufen und Faktor 2 hat J-Stufen. Dann ergibt die Information aus einer Zufallsstichprobe eine allgemeine I × J-Kontingenztabelle, die mit Zeilensummen, Spaltensummen und einer Gesamtsumme wie in Tabelle 11.3 „Allgemeine Kontingenztabelle“ dargestellt aussehen würde. Jede Zelle kann durch ein Paar von Indizes (i,j) gekennzeichnet werden. Oij steht für die beobachtete Anzahl der Beobachtungen in der Zelle in Zeile i und Spalte j, Ri für die i-te Zeilensumme und Cj für die j-te Spaltensumme. Zur Vereinfachung der Notation lassen wir die Indizes weg, so dass Tabelle 11.3 „Allgemeine Kontingenztabelle“ zu Tabelle 11.4 „Vereinfachte allgemeine Kontingenztabelle“ wird. Dennoch ist es wichtig, sich vor Augen zu halten, dass die Os, die Rs und die Cs, obwohl sie mit denselben Symbolen bezeichnet werden, in Wirklichkeit unterschiedliche Zahlen sind.
Tabelle 11.3 Allgemeine Kontingenztabelle
| Faktor 2 Stufen | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Reihe gesamt | ||
| Faktor 1 Stufen | 1 | O11 | – – – | O1j | – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – | Oij | – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OI1 | – – – | OIj | – – – | OIJ | RI | |
| Spalten gesamt | C1 | – – – | Cj | – – – | CJ | n | |
Tabelle 11.4 Vereinfachte allgemeine Kontingenztabelle
| Faktor 2 Stufen | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Zeile Gesamt | ||
| Faktor 1 Stufen | 1 | O | – – – | O | – – – | O | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – | O | – – – | O | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | O | – – – | O | – – – | O | R | |
| Spalte Gesamt | C | – – – | C | – – – | C | n | |
Wie im Beispiel, wird für jede Kernzelle in der Tabelle berechnet, was die erwartete Anzahl E der Beobachtungen wäre, wenn die beiden Faktoren unabhängig wären. E wird für jede Kernzelle (jede Zelle mit einem O darin) der Tabelle 11.4 „Vereinfachte allgemeine Kontingenztabelle“ nach der im Beispiel angewandten Regel berechnet:
wobei R die Zeilensumme und C die Spaltensumme ist, die der Zelle entspricht, und n der Stichprobenumfang ist.
Nachdem die erwartete Anzahl für jede Zelle berechnet wurde, wird die Tabelle 11.4 „Vereinfachte allgemeine Kontingenztabelle“ zu Tabelle 11.5 „Aktualisierte allgemeine Kontingenztabelle“ aktualisiert, indem der berechnete Wert von E in jede Kernzelle eingefügt wird.
Tabelle 11.5 Aktualisierte allgemeine Kontingenztabelle
| Faktor 2 Levels | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – – | J | Zeile Gesamt | ||
| Faktor 1 Stufen | 1 | OE | – – – | OE | – – – | OE | R |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | OE | – – – | OE | – – – | OE | R | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| I | OE | – – – | OE | – – – | OE | R | |
| Spalte gesamt | C | – – – | C | – – | C | n | |
Hier ist die Teststatistik für die allgemeine Hypothese auf der Grundlage von Tabelle 11.5 „Aktualisierte allgemeine Kontingenztabelle“, zusammen mit der Bedingung, dass sie einer Chi-Quadrat-Verteilung folgt.
Teststatistik zur Prüfung der Unabhängigkeit zweier Faktoren
χ2=Σ(O-E)2E
wobei die Summe über alle Kernzellen der Tabelle geht.
Wenn
- die beiden Studienfaktoren unabhängig sind und
- die beobachtete Anzahl O jeder Zelle in Tabelle 11.5 „Aktualisierte allgemeine Kontingenztabelle“ mindestens 5 beträgt,
dann folgt χ2 ungefähr einer Chi-Quadrat-Verteilung mit df=(I-1)×(J-1) Freiheitsgraden.
Die gleichen fünfstufigen Verfahren, entweder der Ansatz des kritischen Wertes oder der Ansatz des p-Wertes, die in Abschnitt 8.1 „Die Elemente des Hypothesentests“ und Abschnitt 8.3 „Die beobachtete Signifikanz eines Tests“ des Kapitels 8 „Testen von Hypothesen“ eingeführt wurden, werden zur Durchführung des Tests verwendet, der immer rechtsschief ist.
Beispiel 1
Ein Forscher möchte untersuchen, ob die Ergebnisse der Schüler in einer College-Aufnahmeprüfung (CEE) eine Aussagekraft für die zukünftigen College-Leistungen haben, die durch den GPA gemessen werden. Mit anderen Worten, er möchte untersuchen, ob die Faktoren CEE und GPA unabhängig sind oder nicht. Er wählt n = 100 Studenten eines Colleges nach dem Zufallsprinzip aus und notiert für jeden Studenten das Ergebnis der Aufnahmeprüfung und seinen Notendurchschnitt am Ende des zweiten Studienjahres. Er teilt die Ergebnisse der Aufnahmeprüfung in zwei Stufen und den Notendurchschnitt in drei Stufen ein. Indem er die Daten nach diesen Unterteilungen sortiert, bildet er die Kontingenztabelle in Tabelle 11.6 „CEE versus GPA Contingency Table“, in der die Zeilen- und Spaltensummen bereits berechnet worden sind.
Tabelle 11.6 CEE versus GPA Contingency Table
| GPA | |||||
|---|---|---|---|---|---|
| <2,7 | 2,7 bis 3,2 | >3.2 | Reihe gesamt | ||
| CEE | <1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Spalte Gesamt | 41 | 36 | 23 | Gesamt=100 | |
Test, auf dem Signifikanzniveau von 1 %, ob diese Daten ausreichende Beweise dafür liefern, dass die CEE-Werte das zukünftige Leistungsniveau von Studienanfängern, gemessen am Notendurchschnitt, anzeigen.
Lösung:
Wir führen den Test mit dem Ansatz des kritischen Wertes durch und folgen dabei der üblichen fünfstufigen Methode, die am Ende von Abschnitt 8.1 „Die Elemente der Hypothesenprüfung“ in Kapitel 8 „Testen von Hypothesen“ beschrieben wird.
-
Schritt 1. Die Hypothesen sind
H0:CEE und GPA sind unabhängige Faktorenvs. Ha:CEE und GPA sind keine unabhängigen Faktoren
- Schritt 2. Die Verteilung ist Chi-Quadrat.
-
Schritt 3. Um den Wert der Teststatistik zu berechnen, müssen wir zunächst die erwartete Zahl für jede der sechs Kernzellen (die, deren Einträge fett gedruckt sind) berechnen:
- 1.Zeile und 1.Spalte: E=(R×C)∕n=41×52∕100=21,32
- 1. Zeile und 2. Spalte: E=(R×C)∕n=36×52∕100=18,72
- 1. Zeile und 3. Spalte: E=(R×C)∕n=23×52∕100=11,96
- 2. Zeile und 1. Spalte: E=(R×C)∕n=41×48∕100=19,68
- 2. Zeile und 2. Spalte: E=(R×C)∕n=36×48∕100=17.28
- 2. Zeile und 3. Spalte: E=(R×C)∕n=23×48∕100=11.04
Tabelle 11.6 „CEE versus GPA Contingency Table“ wird aktualisiert zu Tabelle 11.7 „Updated CEE versus GPA Contingency Table“.
Table 11.7 Aktualisierte CEE versus GPA Kontingenztabelle
GPA <2.7 2.7 bis 3,2 >3,2 Zeile Gesamt CEE <1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Spaltengesamt C = 41 C = 36 C = 23 n = 100 Die Teststatistik ist
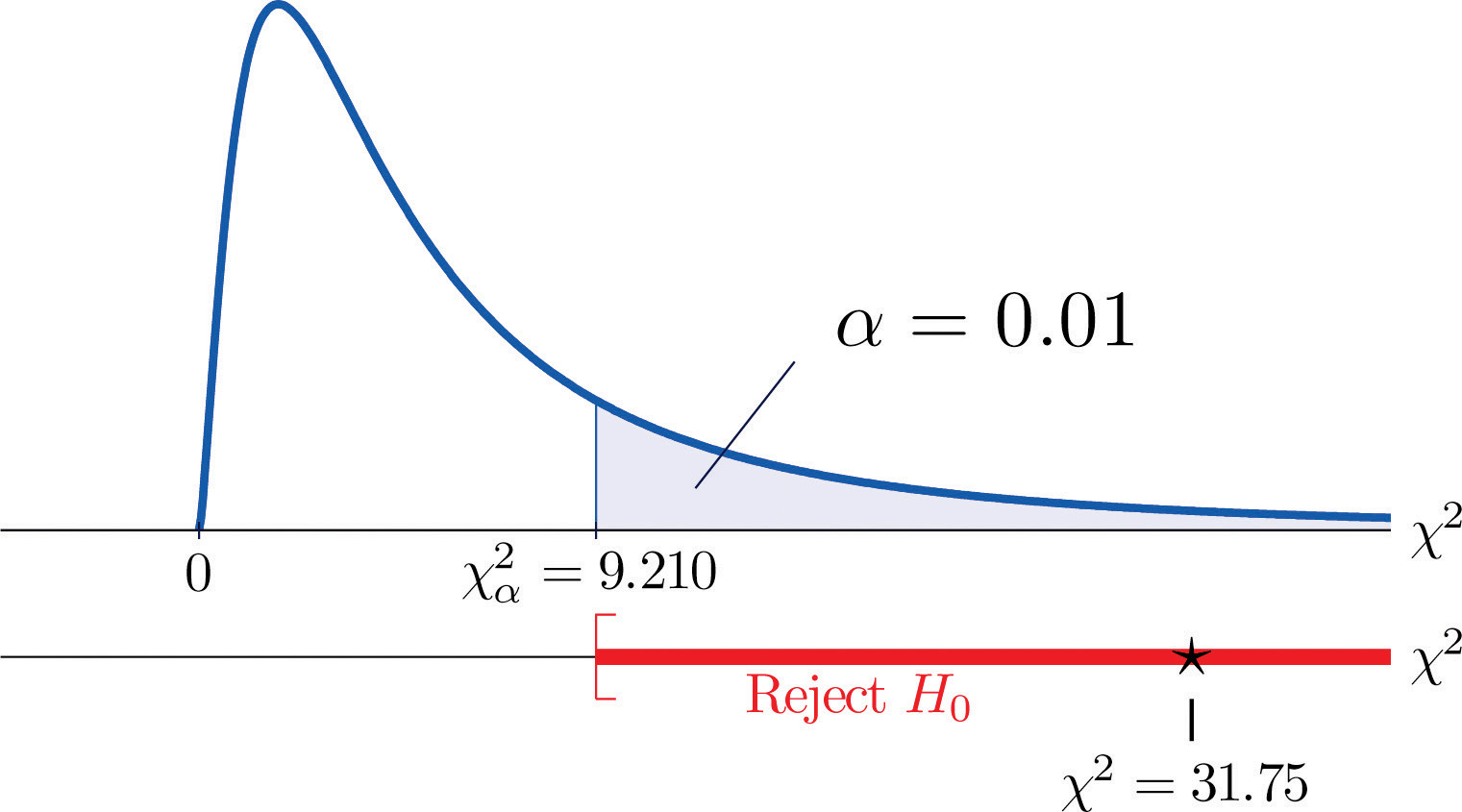
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Da der CEE-Faktor zwei Niveaus hat und der GPA-Faktor drei Niveaus hat, ist I = 2 und J = 3. Somit folgt die Teststatistik der Chi-Quadrat-Verteilung mit df=(2-1)×(3-1)=2 Freiheitsgraden.
Da der Test rechtsschief ist, beträgt der kritische Wert χ0,012. Aus Abbildung 12.4 „Kritische Werte von Chi-Quadrat-Verteilungen“ geht hervor, dass χ0.012=9.210 ist, so dass der Ablehnungsbereich [9.210,∞) ist.
- Schritt 5. Da 31,75 > 9,21 ist die Entscheidung, die Nullhypothese zu verwerfen. Siehe Abbildung 11.4. Die Daten liefern auf dem Signifikanzniveau von 1 % genügend Beweise, um zu dem Schluss zu kommen, dass die CEE-Punktzahl und der Notendurchschnitt nicht unabhängig sind: Die Aufnahmeprüfungspunktzahl hat Vorhersagekraft.
Abbildung 11.4 Anmerkung 11.9 „Beispiel 1“
Key Takeaways
- Kritische Werte einer Chi-Quadrat-Verteilung mit Freiheitsgraden df sind in Abbildung 12 zu finden.4 „Kritische Werte von Chi-Quadrat-Verteilungen“.
- Ein Chi-Quadrat-TestEin Test, der auf einer Chi-Quadrat-Statistik basiert, um zu überprüfen, ob zwei Faktoren unabhängig sind, kann verwendet werden, um die Hypothese zu bewerten, dass zwei Zufallsvariablen oder Faktoren unabhängig sind.
Übungen
-
Bestimmen Sie χ0,012 für jede der folgenden Anzahlen von Freiheitsgraden.
- df=5
- df=11
- df=25
-
Ermitteln Sie χ0,052 für jede der folgenden Anzahlen von Freiheitsgraden.
- df=6
- df=12
- df=30
-
Bestimme χ0.102 für jede der folgenden Anzahl von Freiheitsgraden.
- df=6
- df=12
- df=30
-
Finden Sie χ0.012 für jede der folgenden Anzahl von Freiheitsgraden.
- df=7
- df=10
- df=20
-
Für df=7 und α=0.05, find
- χα2
- χα22
-
Für df=17 und α=0.01, find
- χα2
- χα22
-
Eine Datenstichprobe wird in eine 2 × 2 Kontingenztabelle sortiert, die auf zwei Faktoren basiert, von denen jeder zwei Stufen hat.
Faktor 1 Niveau 1 Ebene 2 Zeile gesamt Faktor 2 Ebene 1 20 10 R Stufe 2 15 5 R Spaltensumme C C n - Finden Sie die Spaltensummen, die Zeilensummen und die Gesamtsumme, n, der Tabelle.
- Ermitteln Sie die erwartete Anzahl E der Beobachtungen für jede Zelle unter der Annahme, dass die beiden Faktoren unabhängig sind (verwenden Sie also einfach die Formel E=(R×C)∕n).
- Ermitteln Sie den Wert der Chi-Quadrat-Teststatistik χ2.
- Ermitteln Sie die Anzahl der Freiheitsgrade der Chi-Quadrat-Teststatistik.
-
Eine Datenstichprobe wird in eine 3 × 2-Kontingenztabelle sortiert, die auf zwei Faktoren basiert, von denen einer drei Stufen und der andere zwei Stufen hat.
Faktor 1 Niveau 1 Niveau 2 Zeile gesamt Faktor 2 Ebene 1 20 10 R Stufe 2 15 5 R Stufe 3 10 20 R Spaltensummen C C n - Finden Sie die Spaltensummen, die Zeilensummen und die Gesamtsumme, n, der Tabelle.
- Bestimmen Sie die erwartete Anzahl E der Beobachtungen für jede Zelle unter der Annahme, dass die beiden Faktoren unabhängig sind (d.h. verwenden Sie einfach die Formel E=(R×C)∕n).
- Bestimmen Sie den Wert der Chi-Quadrat-Teststatistik χ2.
- Ermitteln Sie die Anzahl der Freiheitsgrade der Chi-Quadrat-Teststatistik.
Grundlagen
-
Ein Kinderpsychologe glaubt, dass Kinder bei Tests besser abschneiden, wenn sie eine vermeintliche Wahlfreiheit haben. Um diese Überzeugung zu testen, führte der Psychologe ein Experiment durch, bei dem 200 Drittklässler nach dem Zufallsprinzip in zwei Gruppen eingeteilt wurden, A und B. Jedem Kind wurde der gleiche einfache Logiktest gestellt. In Gruppe B durfte sich jedoch jedes Kind ein Textheft mit verschiedenen Zeichnungen auf dem Einband aussuchen. Die Leistung jedes Kindes wurde mit sehr gut, gut und mittelmäßig bewertet. Die Ergebnisse sind in der beigefügten Tabelle zusammengefasst. Prüfen Sie bei einem Signifikanzniveau von 5 %, ob die Daten ausreichend sind, um die Annahme des Psychologen zu stützen.
Gruppe A B Leistung Sehr gut 32 29 Gut 55 61 Mäßig 10 13 -
In Bezug auf Weinverkostungswettbewerbe, behaupten viele Experten, dass das erste Glas Wein, das serviert wird, einen Referenzgeschmack festlegt und dass ein anderer Referenzwein die relative Rangfolge der anderen Weine im Wettbewerb verändern kann. Um diese Behauptung zu testen, wurden bei einer Weinverkostung drei Weine, A, B und C, serviert. Jedem Teilnehmer wurde ein einziges Glas jedes Weins serviert, jedoch in unterschiedlicher Reihenfolge für die verschiedenen Gäste. Zum Schluss wurde jeder Teilnehmer gebeten, den besten der drei Weine zu nennen. An der Veranstaltung nahmen einhundertzweiundsiebzig Personen teil, deren Top-Auswahl in der Tabelle aufgeführt ist. Testen Sie auf dem Signifikanzniveau von 1 %, ob die Daten genügend Anhaltspunkte für die Behauptung liefern, dass die Präferenz der Weinexperten vom zuerst servierten Wein abhängt.
Top Pick A B C Erstes Glas A 12 31 27 B 15 40 21 C 10 9 7 -
Ist LinkshändigkeitLinkshändigkeit erblich? Zur Beantwortung dieser Frage werden 250 Erwachsene nach dem Zufallsprinzip ausgewählt und ihre Händigkeit sowie die Händigkeit ihrer Eltern notiert. Die Ergebnisse sind in der beigefügten Tabelle zusammengefasst. Testen Sie auf dem Signifikanzniveau von 1 %, ob die Daten genügend Anhaltspunkte für die Schlussfolgerung liefern, dass die Händigkeit vererbbar ist.
Anzahl der Eltern Links-Händer 0 1 2 Händigkeit Links 8 10 12 Rechts 178 21 21 -
Einige Genetiker behaupten, dass die Gene, die die LinkshändigkeitHändigkeit bestimmen, auch die Entwicklung der Sprachzentren des Gehirns steuern. Wenn diese Behauptung wahr ist, dann wäre es vernünftig zu erwarten, dass Linkshänder tendenziell stärkere Sprachfähigkeiten haben. In einer Studie, mit der diese Behauptung überprüft werden sollte, wurden nach dem Zufallsprinzip 807 Studierende ausgewählt, die an der Graduate Record Examination (GRE) teilnahmen. Ihre Ergebnisse im sprachlichen Teil der Prüfung wurden in drei Kategorien eingeteilt: niedrig, durchschnittlich und hoch, und ihre Händigkeit wurde ebenfalls erfasst. Die Ergebnisse sind in der beigefügten Tabelle aufgeführt. Prüfen Sie auf dem Signifikanzniveau von 5 %, ob die Daten genügend Anhaltspunkte dafür liefern, dass Linkshänder tendenziell über bessere sprachliche Fähigkeiten verfügen.
GRE English Scores Low Average Hoch Händigkeit Links 18 40 22 Rechts 201 360 166 Es wird allgemein angenommen, dass Kinder, die in stabilen Familien aufwachsen, in der Regel gute schulische Leistungen erzielen. Um diese Annahme zu überprüfen, untersuchte ein Sozialwissenschaftler die Unterlagen von 290 zufällig ausgewählten Schülern einer öffentlichen High School und notierte die Familienstruktur und den akademischen Status jedes Schülers vier Jahre nach dem Eintritt in die High School. Die Daten wurden dann in eine 2 × 3 Kontingenztabelle mit zwei Faktoren einsortiert. Faktor 1 hat zwei Stufen: Abschluss und kein Abschluss. Faktor 2 hat drei Stufen: kein Elternteil, ein Elternteil und zwei Elternteile. Die Ergebnisse sind in der beigefügten Tabelle aufgeführt. Testen Sie auf dem Signifikanzniveau von 1 %, ob die Daten genügend Anhaltspunkte dafür liefern, dass die Familienstruktur für die schulischen Leistungen der Schüler von Bedeutung ist.
Akademischer Status Abschluss Nicht-Abschluss Familie Kein Elternteil 18 31 Ein Elternteil 101 44 zwei Elternteile 70 26 Die Verwaltung einer großen Mittelschule möchte den Einfluss von Prominenten nutzen, um die Schüler zu ermutigen, in der Schulcafeteria gesündere Entscheidungen zu treffen. Die Cafeteria befindet sich in der Mitte eines offenen Raums. Jeden Tag zur Mittagszeit erhalten die Schüler ihr Mittagessen und ein Getränk in drei separaten Reihen, die zu drei verschiedenen Ausgabestationen führen. Als Experiment hat der Schulverwalter ein Poster eines beliebten Teenager-Popstars aufgehängt, der in jedem der drei Bereiche, in denen Getränke angeboten werden, Milch trinkt, nur dass die Milch auf dem Poster an jedem Ort eine andere ist: eine zeigt weiße Milch, eine zeigt rosa Milch mit Erdbeergeschmack, und eine zeigt Schokoladenmilch. Nach dem ersten Tag des Experiments notierte der Verwalter die Milchauswahl der Schüler getrennt für die drei Linien. Die Daten sind in der beigefügten Tabelle aufgeführt. Testen Sie auf dem Signifikanzniveau von 1 %, ob die Daten genügend Anhaltspunkte dafür liefern, dass die Plakate einen gewissen Einfluss auf die Getränkewahl der Schüler hatten.
Schülerwahl Standard Erdbeere Schokolade Posterwahl Regular 38 28 40 Erdbeere 18 51 24 Schokolade 32 32 53 -
Groß Datensatz 8 enthält das Ergebnis einer Umfrage unter 300 zufällig ausgewählten Erwachsenen, die regelmäßig ins Kino gehen. Für jede Person wurden das Geschlecht und die bevorzugte Art des Films erfasst. Testen Sie auf dem 5 %-Signifikanzniveau, ob die Daten genügend Anhaltspunkte dafür liefern, dass die Faktoren „Geschlecht“ und „bevorzugte Art des Films“ voneinander abhängig sind.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Large Datensatz Übung
Antworten
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0.6698, χ0.052=5.99, nicht verwerfen H0
-
χ2=72.35, χ0.012=9.21, verwerfen H0
-
χ2=21.2784, χ0,012=9,21, verwerfen H0
-
χ2=28,4539. df=3. Ablehnungsbereich: [7.815,∞). Entscheidung: Verwerfe H0 der Unabhängigkeit.