独立性のカイ二乗検定

by

独立性の検定

この本で以前に出会った仮説検定は、二つの母集団のパラメーターの数値がどう比較されるかに関係するものであった。 このサブセクションでは、2つの確率変数が独立して値をとるかどうか、または一方の値が他方の値と関係があるかどうかに関係する仮説を調査します。 したがって、仮説は数学記号ではなく、言葉で表現されます。

胎内にいる赤ちゃんの性別と心拍数が関係しているという説があります。 この説を検証してみたいと思います。 母親の出産前の最後の妊婦健診で撮影された40人の赤ちゃんの心拍記録を調べ、この40人の記録それぞれについて、無作為に選んだ2つの尺度の値を計算する。 1) 性別と2) 心拍数である。 この文脈では、これら2つのランダムな尺度はしばしば因子と呼ばれるいくつかの質的レベルを持つ変数である。 心拍数と性別は無関係ではなく、関係があることを証明する必要があるため、赤ちゃんの性別と心拍数に関する理論の検証問題は以下の仮説の検定として定式化できる：

H0：赤ちゃんの性別と赤ちゃんの心拍数は独立しているvs. Ha:赤ちゃんの性別と心拍数は独立していない

因子の性別は男の子と女の子の2つの自然なカテゴリーまたはレベルを持っている。 第二の因子である心拍数は、ある心拍数、例えば1分間に145回の心拍数を両者の間のカットオフとして選ぶことによって、低いレベルと高いレベルの2つに分割されます。 心拍数が1分間に145回未満は低いと見なされ、145回以上は高いと見なされる。 40件の記録から2×2の分割表ができる。 行の合計、列の合計、そして合計を足し合わせると、表11.1「赤ちゃんの性別と心拍数」のようになる。 太字の4つの項目は、n = 40の標本からのオブザベーションの数である。 心拍数の低い女の子は11人、低い男の子は17人、といった具合である。 これらは展開された表の核を形成している。1 赤ん坊の性別と心拍数

。

心拍数
低い 高い 行合計
性別 女の子 11 7 18
Boy 17 5 22
列合計 28 12 合計 = 40

独立した事象の確率は、それぞれの事象の確率の積であることになぞらえて。 もし心拍数と性別が独立なら、各コアセルの数はそれを含む行と列の合計Rと合計Cの積をサンプルサイズnで割ったものに近いと予想されるでしょう。 このようなオブザベーションの期待数をEとすると，これらの4つの期待値は：

  • 1行と1列． E=(R×C)∕n=18×28∕40=12.6
  • 1 行目、2 列目：E=(R×C)∕n=18×28∕40=12.5 E=(R×C)∕n=18×12∕40=5.4
  • 2 行目、1 列目：E=(R×C)∕n=18×12∕40=5.4 E=(R×C)∕n=22×28∕40=15.4
  • 2 行目、2 列目：E=(R×C)∕n=22×28∕40=15.4 E=(R×C)∕n=22×12∕40=6.6

表11.1「赤ちゃんの性別と心拍数」の更新は、それぞれの期待値を対応するコアセルの観測値の真下に配置することで行います。 これにより、更新された表 表11.2「更新された赤ちゃんの性別と心拍数」

表11.2「更新された赤ちゃんの性別と心拍数」が得られる。2 更新された赤ちゃんの性別と心拍数

Heart Rate
Low高 行合計
性別 女 O=11E=12.6 O=7E=5.4 R=18
Boy O=17E=15.0 O=7E=5.4 Boy O=7E=5.4 O=5E=6.6 R = 22
列合計 C = 28 C = 12 n = 40

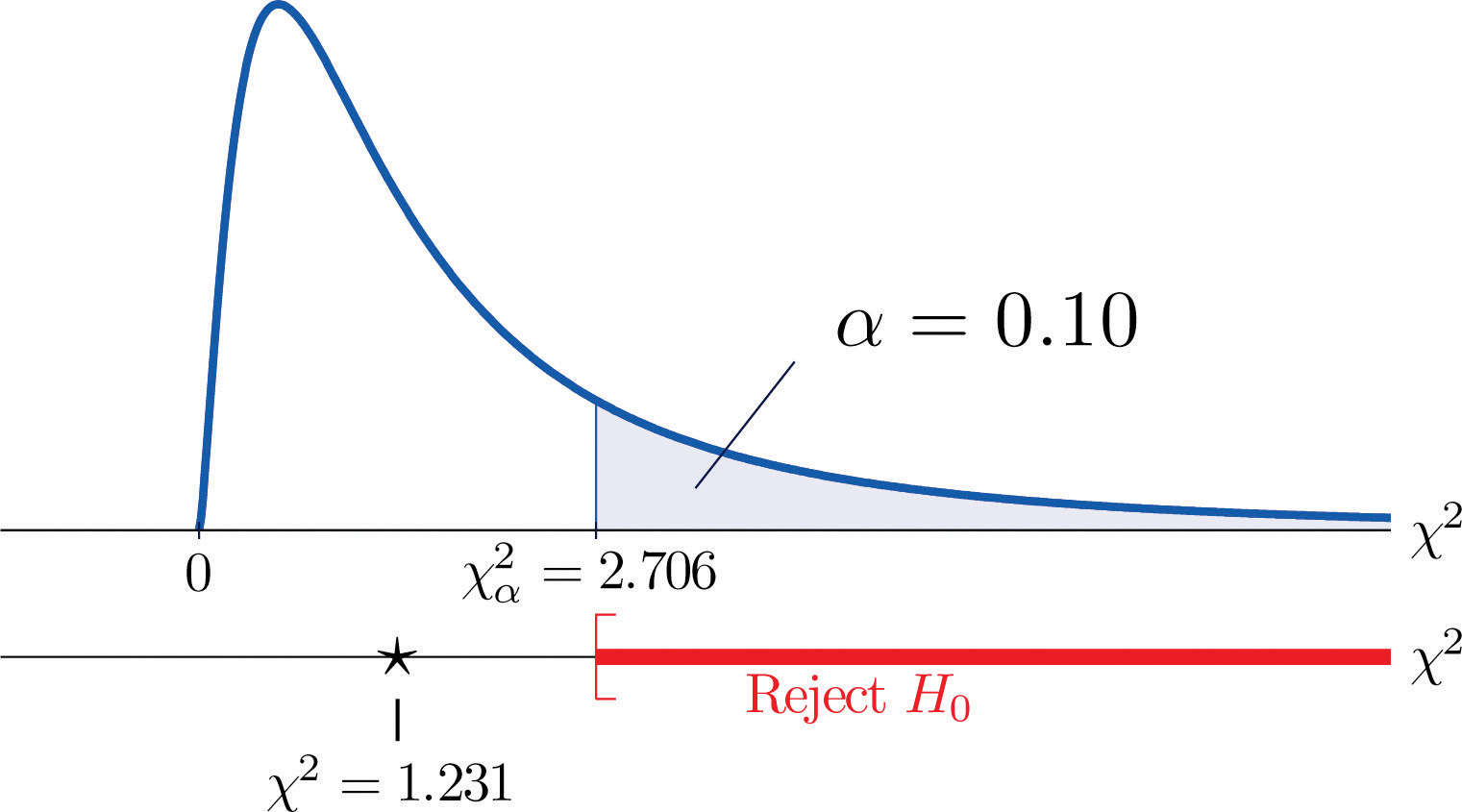
もし因子が本当に独立していた場合にデータがどれだけ予想から外れているか、という指標は各核細胞の数字の差を二乗和にしたものである。 または、各二乗をそのセルの期待数で割って標準化すると、合計Σ(O-E)2∕Eとなる。 我々は、この数が大きい場合にのみ、因子が独立であるという帰無仮説を棄却するだろうから、検定は右側となる。 この例では、確率変数 Σ(O-E)2∕E は、自由度1のカイ2乗分布を持っています。 最初に有意水準10％で検定することにしていた場合、棄却域を定義する臨界値は、図12.4「カイ2乗分布の臨界値」から読み取ると、χα2=χ0.102=2.706となり、棄却域は区間[2.706,∞]になります。 標準化検定統計量の値を計算すると

Σ(O-E)2E=(11-12.6)212.6+(7-5.4)25.4+(17-15.4)215.4+(5-6.6)26.6=1.231

1.231 <2.706 なのでH0は棄却しない判定となる。 図11.3「赤ちゃんの性別予測」参照。 このデータは、10％の有意水準で、心拍数と性別が関係していると結論づけるのに十分な証拠を提供していません。

Figure 11.3 Baby Gender Prediction

この具体例を念頭に置いて、今度は一般論に目を向けてみましょう。 因子1、因子2と呼ぶ2つの因子の独立性を検定するという一般的な設定で、検定する仮説は

H0：2つの因子は独立しているvs.H2：2つの因子は独立しているvs. Ha:2つの因子は独立していない

例のように、各因子はいくつかのカテゴリまたはレベルに分割されます。 これらは性別の少年少女区分のように自然に発生することもあれば、心拍数の高低区分のように多少恣意的に発生することもある。 例えば、因子1がIレベル、因子2がJレベルであるとする。 この表は行の合計、列の合計、総計で表11.3「一般分割表」に示すようになります。 各セルは一対の添字(i,j)でラベル付けされる。 Oij は，セル内の行i と列j のオブザベーションの観察されたカウントを表し，Ri はi番目の行合計，Cj はj番目の列合計を表す． 表記を簡単にするために、インデックスを削除するので、表 11.3 「一般分割表」は表 11.4 「簡易一般分割表」となる。 ただし、Os、Rs、Csは同じ記号で表されているが、実際には異なる数字であることに注意する必要がある。3 一般コンティンジェンシー表

行合計

– – – – –

– –

– – –

の場合

ファクター2レベル
1 – – J 行合計 J
ファクター1レベル 1 O11 – – O1j – – O1J R1
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
i Oi1 – – Oij – – OiJ Ri
Oi1 Oij Ri
Oi1⋮ ⋮ ⋮
i oi1 – – OIj RI
列の合計 C1 – – Cj – – Cj n

表11.CJ

Cj n

Cj

– – –

– –

因子2レベル
1 – – j – – J 行合計
ファクター1レベル 1 O – – – – o r
⋮ ⋮ ⋮ ⋮ ⋨ ⋨ ⋨ ⋨ ⋨ ˨ ˨ ˨
i O – – – O R
O O R R 。 ⋮ ⋮ ⋮
i o ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ O R
列の合計 C – – C – – n

例と同様。 表の各コア・セルについて、2つの因子が独立である場合のオブザベーションの期待数Eが何であるかを計算する。 Eは表11.4「簡易一般分割表」の各中核セル(Oを含む各セル)について例で適用したルールで計算されます：

E=R×Cn

ここでRは行合計、Cはセルに対応する列合計、nはサンプルサイズとします。

各セルについて期待数を計算した後、表11.4「簡略化した一般分割表」を更新し、計算したEを各コアセルに挿入して表11.5「更新した一般分割表」とする。5 更新されたコンティンジェンシー表

1

の場合

Factor 2 Levels
– – j – – J 行合計
ファクター1レベル 1 OE – – OE – – R
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
i oe – – – oe – – – r
⋮ ⋮ ⋮ ⋮ ⋮
i oe – – oe – – OE R
列合計 C – – – C -の場合。 – C n

ここで、表11に基づく一般仮説の検定統計量について説明する。

Test Statistic for Testing the Independence of Two Factors

χ2=Σ(O-E)2E

ここで、合計は表のすべてのコアセルにわたっています。

二つの試験要因が独立で、

  • 表11.5「更新した一般分割表」の各セルの観測数Oが少なくとも5であれば、

    • χ2は近似的にdf＝（I-1）×（J-1）自由度を持つカイ二乗分布に従うことになります。

    第8章「仮説の検定」の8.1節「仮説検定の要素」および8.3節「検定の観察された有意性」で紹介した臨界値法またはp値法と同じ5段階の手順で検定を行い、常に右側となるように検定する。

    例1

    ある研究者が、大学入学試験（CEE）の点数が、GPAで測った将来の大学の成績に対して何らかの示唆力を持つかどうかを調査したい、と考えている。 言い換えれば、CEEとGPAが独立した因子であるか否かを調査したい。 彼は、ある大学の学生を無作為にn=100人選び、それぞれの学生の入試の得点と2年生終了時のGPAを記録する。 彼は、入試の得点を2つのレベルに、評定平均値を3つのレベルに分ける。 これらの区分に従ってデータを並べ替えると、表11.6「CEE対GPA分割表」のようになり、行と列の合計がすでに計算されている。

    表11.6 CEE対GPA分割表

    に変更。

    GPA
    <2.7 2.7→3.2 >3.7→3.23.22 行合計
    CEE 1800 35 12 5 52
    ≧1800 6 24 18 48
    列合計 41 36 23 合計=100

    テスト, これらのデータは、CEEの得点がGPAで測定される大学新入生の将来の成績レベルを示すと結論づけるに十分な証拠を提供するかどうかを、有意水準1%で検討する。

    解答：

    我々は、第8章「仮説の検証」の第8.1節「仮説検証の要素」の最後に概説した通常の5ステップ法に従って、臨界値法を用いて検定を行う

    • ステップ1. 仮説は

      H0:CEEとGPAは独立因子vs.Ha:CEEとGPAは独立因子ではない

    • Step 2. 分布はカイ二乗である

    • ステップ3. 検定統計量を計算するには、まず6つのコアセル（項目が太字になっているもの）ごとに期待値を計算しなければなりません：

      • 1 行目、1 列目。 E=(R×C)∕n=41×52∕100=21.32
      • 1 行目、2 列目：E=(R×C)∕n=21.32。 E=(R×C)∕n=36×52∕100=18.72
      • 1 行目、3 列目：E=(R×C)∕n=36×52∕100=18.72 E=(R×C)∕n=23×52∕100=11.96
      • 2 行目、1 列目：E=(R×C)∕n=23×52∕100=11.96 E=(R×C)∕n=41×48∕100=19.68
      • 2 行目、2 列目。 E=(R×C)∕n=36×48∕100=17.28
      • 2 行目、3 列目：E=(R×C)∕n=36×48∕100=17.28 E=(R×C)∕n=23×48∕100=11.04

      表 11.6 “CEE vs GPA Contingency Table” を表 11.7 “Updated CEE vs GPA Contingency Table” に更新。

      表 11.6 “E vs GPA Contingency Table” を更新。7 Updated CEE versus GPA Contingency Table

      >>3.13.2>3.23.2>

      。04

      GPA
      <2.7 2.7.7～3.2 >3.2 行合計
      CEE <1800 O=35E=21.1 3.2>3.2 O=12E=18.72 O=5E=11.96 r = 52
      ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.0
      O=24E=16.0 O=18E=16.0 R = 48
      列合計 C = 41 C = 36 C = 23 n = 100

      検定統計量は

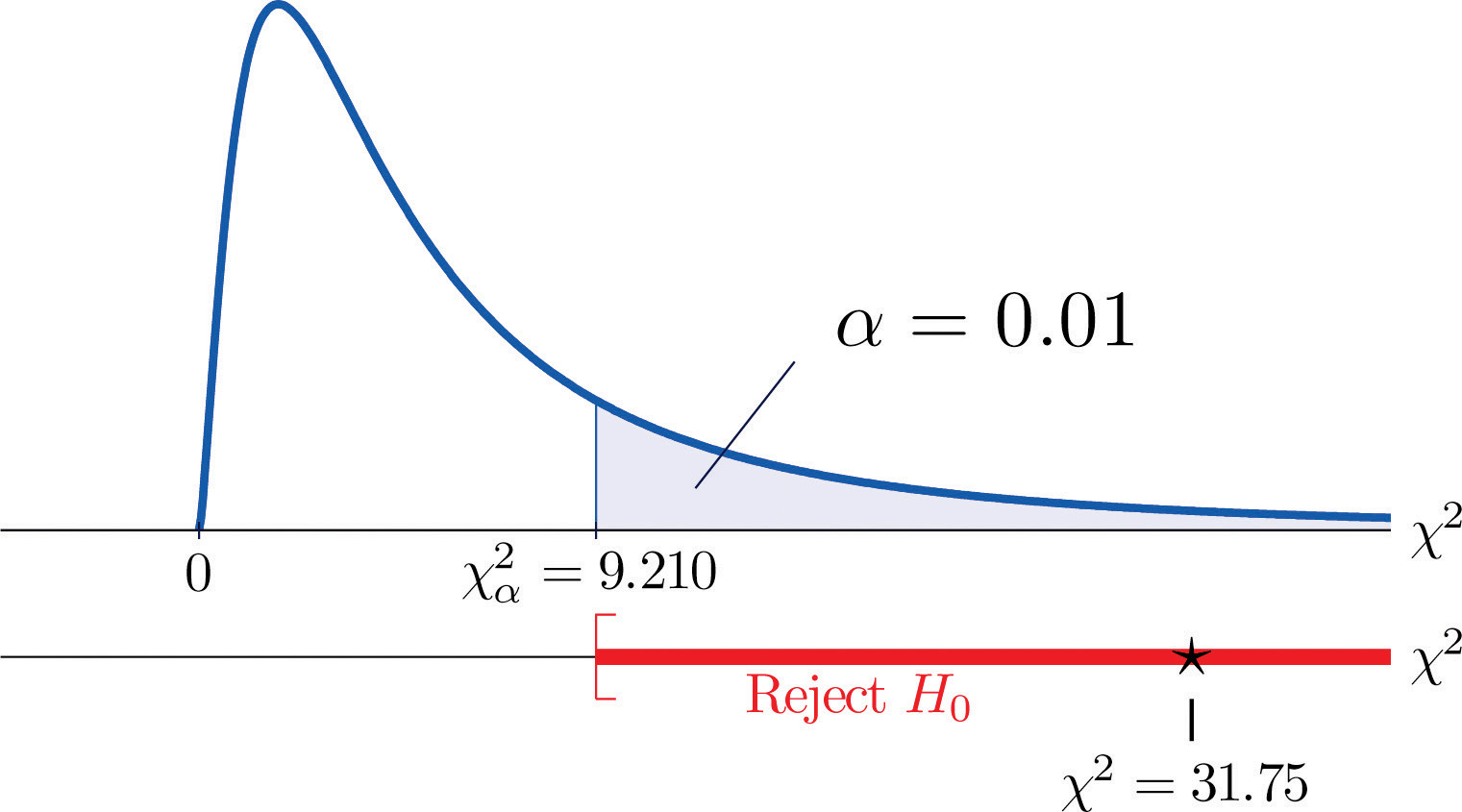
      χ2=Σ（O-E)2E=（35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75

    • Step 4. CEE因子は2水準、GPA因子は3水準なので、I＝2、J＝3。 よって、検定統計量はdf=(2-1)×(3-1)=2の自由度を持つカイ二乗分布に従う。

      検定が右側なので、臨界値はχ0.012です。 図12.4「カイ二乗分布の臨界値」から読み取ると、χ0.012=9.210なので、棄却域は［9.210，∞］となります。 31.75 > 9.21なので、帰無仮説を棄却することが決定されます。 図11.4を参照してください。 このデータは、1%の有意水準で、CEEスコアとGPAは独立ではないと結論づけるのに十分な証拠を提供している：入試スコアは予測力を持つ。

    図11.4 注11.9「例1」

    Key Takeaways

    • 自由度dfのカイ二乗分布の限界値は、図12にある。4「カイ二乗分布の臨界値」
    • カイ二乗検定2つの要因が独立しているかどうかを調べるためのカイ二乗統計量に基づく検定。2つの確率変数または要因が独立しているという仮説を評価するために使用することができる。

    演習

      基礎

    1. 次の自由度数のそれぞれについてχ0.012を求めよ。

      1. df=5
      2. df=11
      3. df=25

    2. 以下の自由度の数に対してそれぞれχ0.052を探してみてください。

      1. df=6
      2. df=12
      3. df=30

    3. χ0.052を探してください。以下の自由度数のそれぞれについて102。

      1. df=6
      2. df=12
      3. df=30

    4. χ0を求めよ。012は次の自由度数ごとに求めよ。

      1. df=7
      2. df=10
      3. df=20

    5. df=7、α=0のとき…。05, find

      1. χα2
      2. χα22

    6. df=17、α=0.の場合、α=0.の場合、α=0.の場合、α=0.の場合、α=0.の場合、α=0.の場合、α=0.の場合、α=0.の場合。01, find

      1. χα2
      2. χα22

      7. データサンプルは2×2の分割表に、それぞれ2水準を持つ因子に基づいて分類されます。

      に分類される。

      の場合

      Factor 1
      レベル1 レベル2 行合計
      ファクター2 レベル1 20 10 R
      レベル2 15 5 R
      列合計 C n
      1. 列合計を検索します。 行の合計、および表の総計であるnを計算します。
      2. 2つの要因が独立であると仮定して、各セルの観測値の期待値Eを求める（つまり、E=(R×C)∕nの公式を使えばよい）
      3. カイ二乗検定の統計量χ2 の値を求める。
      4. カイ二乗検定統計量の自由度数を求めよ。

  • データサンプルが、3水準を持つものと2水準を持つものの二つの要因に基づいて3×2分割表に分類される。

    となる。

    の順です。

    の場合

    因子1
    レベル1 レベル2 行合計
    係数2 レベル1 20 10 R
    レベル2 15 5 R
    レベル3 10 20 R
    列合計 C n
    1. 列合計を検索します。 行の合計、および表の総計であるnを計算します。
    2. 2つの要因が独立であると仮定して、各セルの観測値の期待値Eを求める（つまり、E=(R×C)∕nの公式を使えばよい）
    3. カイ二乗検定統計量χ2の値を求めよ。
    4. カイ二乗検定統計量の自由度数を求めよ。

      • Applications

    1. ある児童心理学者は、子供は選択の自由が与えられるとテストで良い結果を出すと信じている。 この心理学者は、この信念を検証するために、200人の小学3年生をAとBの2つのグループにランダムに振り分け、それぞれの子供に同じ簡単な論理テストをさせるという実験を行った。 しかし、Bのグループには、表紙にいろいろな絵が描かれた冊子の中から自由にテキストを選んでもらった。 各子供の成績は、「とても良い」「良い」「まあまあ」の3段階で評価された。 その結果を表にまとめました。 心理学者の信念を支持する十分な証拠がデータにあるかどうか、5%の有意水準で検定しなさい。

      の順で表示。

      グループ
      A B
      パフォーマンス Very Good 32 29
      Good 55 61
      Fair 10 13

    2. ワイン試飲会に関してです。 多くの専門家は、最初に提供されるワインが基準となる味を設定し、基準となるワインが異なれば、他のワインの相対的な順位が変化する可能性があると主張している。 この主張を検証するために、あるワインテイスティングイベントでA、B、Cの3つのワインが提供された。 各人にはそれぞれのワインが1杯ずつ提供されたが、ゲストによってその順番は異なった。 最後に、3つのワインの中で一番おいしいものを挙げるよう、各自に求めた。 172人がこのイベントに参加し、彼らが一番に選んだワインは、提供された表に示されています。 ワインの専門家の好みが最初に出されたワインに依存するという主張を支持する十分な証拠がデータにあるかどうか、1%の有意水準で検定してください。

      。

      Top Pick
      A B C
      ファーストグラス A 12 31 27
      b 15 40 21
      c 10 9 7

    3. 左利きなのか？手先の器用さは遺伝するのか？ この問いに答えるため、250人の成人を無作為に選び、彼らの手の大きさと両親の手の大きさを記録しています。 その結果は、提供された表にまとめられています。 このデータから、手の大きさには遺伝的要素があると結論付けるに足る証拠があるかどうかを、1%の有意水準で検定してください。

      」。

      両親の数 左利き利き手
      0 1 2
      手の向き 左 8 10 12
      右 178 21

    4. 一部の遺伝学者は、左を決定する遺伝子は、左を決定すると主張しています。利き手は、脳の言語中枢の発達も支配している。 もしこの主張が本当なら、左利きの人は言語能力が高い傾向にあると予想するのは妥当だろう。 この主張を検証するために計画された研究では、大学院進学適性試験（GRE）を受験した807人の学生を無作為に選びました。 この研究では、GRE（Graduate Record Exam）を受験した807人の学生を無作為に抽出し、言語分野のスコアを「低い」「平均」「高い」の3つのカテゴリーに分類し、さらにその人の利き手を記録しています。 その結果を表に示します。 左利きの人は言語能力が高い傾向があると結論づけるに足る証拠がデータにあるかどうか、5％の有意水準で検定しなさい。

      の順。

      GRE English Scores
      Low Average 高
      手の大きさ 左 18 40 22
      Right 201 360 166

    5. 一般的には安定した家庭に育った子供は学業成績が良い傾向があると言われています。 このような信念を検証するために、ある社会科学者は、無作為に選んだ290人の公立高校の生徒の記録を調べ、各生徒の家族構成と高校入学後4年間の学業状況を記した。 そして、そのデータを2×3の分割表に並べ替え、2つの要素を持つようにした。 第1因子は、卒業と未卒業の2水準である。 第2因子は、「親なし」「片親」「二親」の3水準である。 その結果は、提供された表に示されている。 家族構成が生徒の学業成績に重要であると結論づけるに足る証拠がデータにあるかどうか、有意水準1%で検定しなさい。

      の場合

      学業状況
      卒業した 卒業しなかった
      家族 親なし 18 31
      親1人 101 44
      2 人の親 70 26

    6. 大きな中学校の管理者は学校のカフェテリアで生徒により健康な選択をするように有名人を利用したいと考えています。 カフェテリアはオープンスペースの中央に位置しています。 毎日昼休みになると、生徒たちは3つの給仕ステーションに続く3つの列で弁当と飲み物を手にする。 しかし、ポスターに写っている牛乳は、白い牛乳、イチゴ味のピンク色の牛乳、チョコレート色の牛乳と、それぞれ異なっているのです。 実験初日の後、管理者は生徒が選んだミルクを3つの行に分けて記録した。 そのデータは、提供された表に示されています。 ポスターが生徒の飲み物の選択に何らかの影響を与えたと結論付けるに足る証拠がデータにあるかどうかを、有意水準1%で検定しなさい。

      の場合

      学生の選択
      普通 イチゴ チョコレート
      ポスターチョイス
      レギュラー 38 28 40
      ストロベリー 18 51 24
      Chocolate 32 53

        Large データセット演習

      1. Large データセット8は、映画館によく行く成人300人を無作為に選んで調査した結果を記録しています。 各人について、性別と好みの映画の種類が記録されている。 性別」と「好きな映画の種類」という要素が依存関係にあると結論付けるに足る証拠がデータにあるかどうかを、有意水準5％で検定せよ。

        http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls

      回答

        1. 15.09,

        1. 24.72,
        2. 44.31
        1. 10.64,
        2. 18.55,
        3. 40.26
        1. 14.07,
        2. 16.01
        4. C1=35,C2=15,R1=30,R2=20,n=50,

        1. E11=21,E12=9,E21=14,E22=6,

          2. χ2=0.0.3968,

        2. df=1

      1. χ2=0.6698, χ0.0.052=5.99、棄却しない H0

      2. χ2=72.35, χ0.012=9.21, 除外 H0

      3. χ2=21.0, χ0.012=2.0, 除外 H1

      4. χ2=21.02784, χ0.012=9.21, reject H0

      1. χ2=28.4539. df=3.である。 拒絶反応領域。 [7.815,∞). 決定。 独立性のH0を棄却する.

    コメントする