Teste Chi-Square pentru independență

Teste de independență

Testele de ipoteză întâlnite mai devreme în carte aveau legătură cu modul în care se comparau valorile numerice a doi parametri ai populației. În această subsecțiune vom cerceta ipoteze care au legătură cu faptul dacă două variabile aleatoare își iau sau nu valorile în mod independent sau dacă valoarea uneia are o relație cu valoarea celeilalte. Astfel, ipotezele vor fi exprimate în cuvinte, nu în simboluri matematice. Construim discuția în jurul următorului exemplu.

Există o teorie conform căreia sexul unui copil în uter este legat de ritmul cardiac al copilului: fetițele tind să aibă un ritm cardiac mai ridicat. Să presupunem că dorim să testăm această teorie. Examinăm înregistrările ritmului cardiac a 40 de bebeluși luate în timpul ultimelor controale prenatale ale mamelor lor înainte de naștere și, pentru fiecare dintre aceste 40 de înregistrări selectate aleatoriu, calculăm valorile a două măsuri aleatorii: 1) sexul și 2) ritmul cardiac. În acest context, aceste două măsuri aleatorii sunt adesea numite factoriO variabilă cu mai multe niveluri calitative… Deoarece sarcina probei este că frecvența cardiacă și sexul sunt legate, nu că nu sunt legate, problema testării teoriei privind sexul și frecvența cardiacă a bebelușului poate fi formulată ca un test al următoarelor ipoteze:

H0:Sexul și frecvența cardiacă a bebelușului sunt independentevs. Ha:Sexul bebelușului și ritmul cardiac al bebelușului nu sunt independente

Factorul sex are două categorii sau niveluri naturale: băiat și fată. Împărțim al doilea factor, ritmul cardiac, în două niveluri, scăzut și ridicat, alegând o anumită frecvență cardiacă, să zicem 145 bătăi pe minut, ca limită între ele. Un ritm cardiac mai mic de 145 bătăi pe minut va fi considerat scăzut, iar 145 și peste va fi considerat ridicat. Cele 40 de înregistrări dau naștere unui tabel de contingență 2 × 2. Prin alăturarea totalurilor de rânduri, a totalurilor de coloane și a unui total general se obține tabelul prezentat în Tabelul 11.1 „Sexul copilului și ritmul cardiac”. Cele patru intrări cu caractere aldine sunt numărători de observații din eșantionul de n = 40. Au existat 11 fete cu ritm cardiac scăzut, 17 băieți cu ritm cardiac scăzut și așa mai departe. Ele formează nucleul tabelului extins.

Tabelul 11.1 Sexul bebelușului și frecvența cardiacă

		Frecvența cardiacă
		Frecvența cardiacă scăzută	Frecvența cardiacă ridicată	Total rând
Gender	Fată	11	7	18
Gender	Băiat	17	5	22
Total coloană		28	12	Total = 40

În analogie cu faptul că probabilitatea unor evenimente independente este produsul probabilităților fiecărui eveniment, dacă frecvența cardiacă și sexul sunt independente, atunci ne-am aștepta ca numărul din fiecare celulă centrală să fie apropiat de produsul dintre totalul rândului R și totalul coloanei C ale rândului și coloanei care o conțin, împărțit la dimensiunea eșantionului n. Denumindu-se un astfel de număr așteptat de observații E, aceste patru valori așteptate sunt:

1rândul 1 și coloana 1: E=(R×C)∕n=18×28∕40=12,6
1rândul 1 și coloana 2: E=(R×C)∕n=18×12∕40=5,4
Rândul 2 și coloana 1: E=(R×C)∕n=18×12∕40=5,4
Rândul 2 și coloana 1: E=(R×C)∕n=22×28∕40=15,4
Rândul 2 și coloana 2: E=(R×C)∕n=22×28∕40=15,4
Rândul 2 și coloana 2: E=(R×C)∕n=22×28∕40=15,4 E=(R×C)∕n=22×12∕40=6,6

Actualizăm tabelul 11.1 „Sexul bebelușului și ritmul cardiac” prin plasarea fiecărei valori așteptate în celula centrală corespunzătoare, chiar sub valoarea observată în celulă. Se obține astfel tabelul actualizat Tabelul 11.2 „Sexul bebelușului și frecvența cardiacă actualizate”.

Tabelul 11.2 Sexul bebelușului și frecvența cardiacă actualizate

		Frecvența cardiacă
		Low	Superioară	Total rând
Gender	Fată	O=11E=12.6	O=7E=5.4	R = 18
Gender	Băiat	O=17E=15.4	O=5E=6.6	R = 22
Total coloană		C = 28	C = 12	n = 40

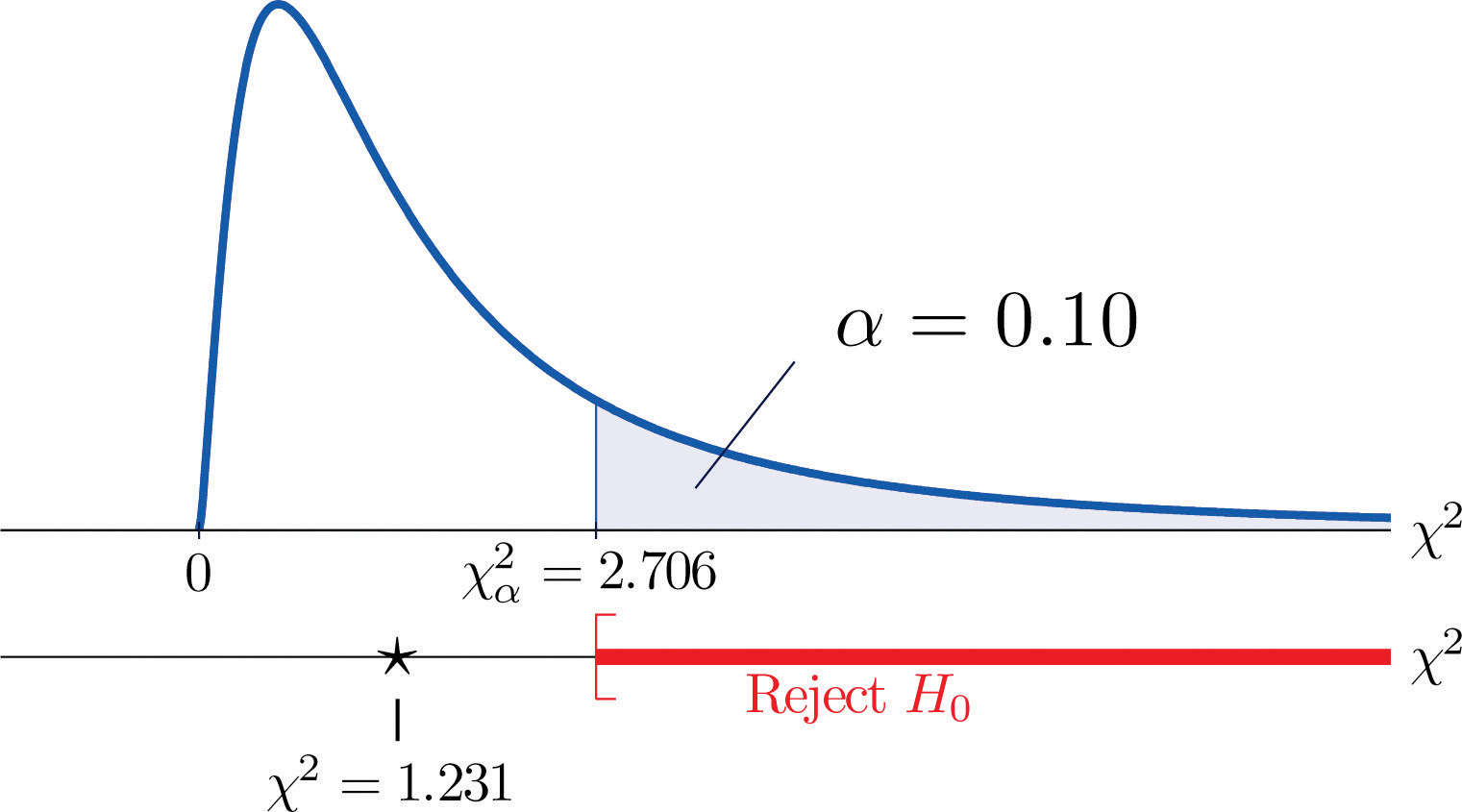
O măsură a cât de mult se abat datele de la ceea ce ne-am aștepta să vedem dacă factorii ar fi cu adevărat independenți este suma pătratelor diferenței numerelor din fiecare celulă centrală, sau, standardizând prin împărțirea fiecărui pătrat la numărul așteptat în celula respectivă, suma Σ(O-E)2∕E. Am respinge ipoteza nulă conform căreia factorii sunt independenți numai dacă acest număr este mare, astfel încât testul are coada dreaptă. În acest exemplu, variabila aleatoare Σ(O-E)2∕E are distribuția chi-pătrat cu un grad de libertate. Dacă am fi decis de la început să testăm la un nivel de semnificație de 10%, valoarea critică ce definește regiunea de respingere ar fi, citind din figura 12.4 „Valori critice ale distribuțiilor chi pătrat”, χα2=χ0,102=2,706, astfel încât regiunea de respingere ar fi intervalul [2,706,∞). Când calculăm valoarea statisticii standardizate a testului obținem

Σ(O-E)2E=(11-12.6)212.6+(7-5.4)25.4+(17-15.4)215.4+(5-6.6)26.6=1.231

Din moment ce 1.231 < 2.706, decizia este de a nu respinge H0. A se vedea figura 11.3 „Predicția sexului copilului”. Datele nu oferă suficiente dovezi, la un nivel de semnificație de 10%, pentru a concluziona că frecvența cardiacă și sexul sunt legate.

Figura 11.3 Predicția sexului bebelușului

Cu acest exemplu specific în minte, trecem acum la situația generală. În cadrul general de testare a independenței a doi factori, numiți Factorul 1 și Factorul 2, ipotezele care trebuie testate sunt

H0:Cei doi factori sunt independențivs. Ha:Cei doi factori nu sunt independenți

Ca în exemplu, fiecare factor este împărțit într-un număr de categorii sau niveluri. Acestea ar putea apărea în mod natural, ca în diviziunea băiat-fată a sexului, sau oarecum arbitrar, ca în diviziunea înalt-jos a ritmului cardiac. Să presupunem că factorul 1 are nivelurile I și factorul 2 are nivelurile J. Atunci, informațiile dintr-un eșantion aleatoriu dau naștere unui tabel general de contingență I × J, care, cu totalurile rândurilor, totalurile coloanelor și un total general, ar apărea așa cum se arată în tabelul 11.3 „Tabel general de contingență”. Fiecare celulă poate fi etichetată cu o pereche de indici (i,j). Oij reprezintă numărul de observații observate în celulă în rândul i și coloana j, Ri pentru al i-lea total al rândului și Cj pentru al j-lea total al coloanei. Pentru a simplifica notația, vom renunța la indici, astfel încât tabelul 11.3 „Tabel general de contingență” devine tabelul 11.4 „Tabel general de contingență simplificat”. Cu toate acestea, este important să reținem că O, R și C, deși sunt notate cu aceleași simboluri, sunt de fapt numere diferite.

Tabel 11.3 Tabel general de contingență

		Nivelurile factorului 2
		1	– – – –	j	– – – –	J	Total rând
Factor 1 Niveluri	1	O11	– – – –	O1j	– – – –	O1J	R1
	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	i	Oi1	– – – –	Oij	– – – –	OiJ	Ri
	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	I	OI1	– – – –	OIj	– – – –	OIJ	RI
Total coloană		C1	– – – –	Cj	– – – –	CJ	n

Tabelul 11.4 Tabel simplificat de contingență generală

		Nivelurile factorului 2
		1	– – – –	j	– – – –	J	Total rând
Factor 1 Niveluri	1	O	– – – –	O	– – – –	O	R
	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	i	O	– – – –	O	– – – –	O	R
	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	I	O	– – – –	O	– – – –	O	R
Total coloană		C	– – – – –	C	– – – – –	C	n

Ca în exemplu, pentru fiecare celulă centrală din tabel calculăm care ar fi numărul așteptat E de observații dacă cei doi factori ar fi independenți. E se calculează pentru fiecare celulă centrală (fiecare celulă cu un O în ea) din tabelul 11.4 „Tabel general simplificat de contingență” prin regula aplicată în exemplu:

E=R×Cn

unde R este totalul rândurilor și C este totalul coloanelor corespunzătoare celulei, iar n este dimensiunea eșantionului.

După ce numărul așteptat este calculat pentru fiecare celulă, tabelul 11.4 „Tabel de contingență generală simplificat” este actualizat pentru a forma tabelul 11.5 „Tabel de contingență generală actualizat” prin inserarea valorii calculate a lui E în fiecare celulă centrală.

Tabelul 11.4 „Tabel de contingență generală simplificat” este actualizat pentru a forma tabelul 11.5 „Tabel de contingență generală actualizat” prin inserarea valorii calculate a lui E în fiecare celulă centrală.5 Tabel general actualizat al contingențelor

		Nivelurile factorului 2
		1	– – – –	j	– – – –	J	Total rând
Nivelurile factorului 1	1	OE	– – – –	OE	– – – –	OE	R	R
	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	i	OE	– – – –	OE	– – – – –	OE	R
	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
	I	OE	– – – –	OE	OE	– – – –	OE	R
Total coloană		C	– – – –	C	– – –	C	– –	C	n

Iată statistica de test pentru ipoteza generală bazată pe tabelul 11.5 „Tabel general de contingență actualizat”, împreună cu condițiile ca aceasta să urmeze o distribuție chi-pătrat.

Statistică de test pentru testarea independenței a doi factori

χ2=Σ(O-E)2E

unde suma este peste toate celulele de bază ale tabelului.

Dacă

cei doi factori de studiu sunt independenți și
numărul observat O din fiecare celulă din tabelul 11.5 „Tabel de contingență general actualizat” este de cel puțin 5,

atunci χ2 urmează aproximativ o distribuție chi-pătrat cu df=(I-1)×(J-1) grade de libertate.

Pentru efectuarea testului, care are întotdeauna coada dreaptă, se folosesc aceleași proceduri în cinci pași, fie abordarea valorii critice, fie abordarea valorii p, care au fost introduse în secțiunea 8.1 „Elementele testării ipotezelor” și în secțiunea 8.3 „Semnificația observată a unui test” din capitolul 8 „Testarea ipotezelor”.

Exemplu 1

Un cercetător dorește să investigheze dacă notele obținute de elevi la un examen de admitere la facultate (CEE) au vreo putere indicativă pentru performanțele viitoare la facultate, măsurate prin media generală. Cu alte cuvinte, el dorește să investigheze dacă factorii CEE și GPA sunt independenți sau nu. El selectează în mod aleatoriu n = 100 de studenți dintr-un colegiu și notează scorul fiecărui student la examenul de admitere și media sa la sfârșitul celui de-al doilea an de facultate. El împarte scorurile de la examenul de admitere în două niveluri și mediile notelor în trei niveluri. Ordonând datele în funcție de aceste diviziuni, el formează tabelul de contingență prezentat în Tabelul 11.6 „Tabel de contingență CEE versus GPA”, în care totalurile rândurilor și coloanelor au fost deja calculate.

Tabel 11.6 Tabel de contingență CEE versus GPA

		GPA
		<2,7	2,7 până la 3,2	>3.2	Rândul Total
CEE	1800	35	12	5	5	52
CEE	≥1800	6	24	18	48
Total coloană		41	36	23	Total=100

Test, la nivelul de semnificație de 1%, dacă aceste date oferă suficiente dovezi pentru a concluziona că scorurile CEE indică nivelurile de performanță viitoare ale bobocilor care intră la facultate, măsurate prin GPA.

Soluție:

Realizăm testul folosind abordarea valorii critice, urmând metoda obișnuită în cinci pași prezentată la sfârșitul secțiunii 8.1 „Elementele testării ipotezelor” din capitolul 8 „Testarea ipotezelor”.

Pasul 1. Ipotezele sunt

H0:CEE și GPA sunt factori independențivs. Ha:CEE și GPA nu sunt factori independenți
Pasul 2. Distribuția este chi-pătrat.

Etapa 3. Pentru a calcula valoarea statisticii de test trebuie să calculăm mai întâi numărul așteptat pentru fiecare dintre cele șase celule de bază (cele ale căror intrări sunt scrise cu bold):

1rândul 1 și coloana 1: E=(R×C)∕n=41×52∕100=21,32
1-lea rând și a 2-a coloană: E=(R×C)∕n=36×52∕100=18.72
1rândul 1 și coloana 3: E=(R×C)∕n=23×52∕100=11.96
Rândul al 2-lea și coloana 1: E=(R×C)∕n=23×48∕100=11,04

Tabelul 11.6 „CEE versus GPA Contingency Table” se actualizează în Tabelul 11.7 „Updated CEE versus GPA Contingency Table”.

Tabelul 11.7 „Updated CEE versus GPA Contingency Table”.7 Tabel actualizat CEE versus GPA Contingency Table

		GPA
		<2.7	2.7 la 3,2	>3,2	Rândul Total
CEE	1800	O=35E=21.32	O=12E=18.72	O=5E=11.96	R = 52
CEE	≥1800	O=6E=19.68	O=24E=17.28	O=18E=11.28	O=18E=11.04	R = 48
Total coloană		C = 41	C = 36	C = 23	n = 100

Statistica testului este

χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75

Step 4. Deoarece factorul CEE are două niveluri, iar factorul GPA are trei, I = 2 și J = 3. Astfel, statistica testului urmează distribuția chi-pătrat cu df=(2-1)×(3-1)=2 grade de libertate.

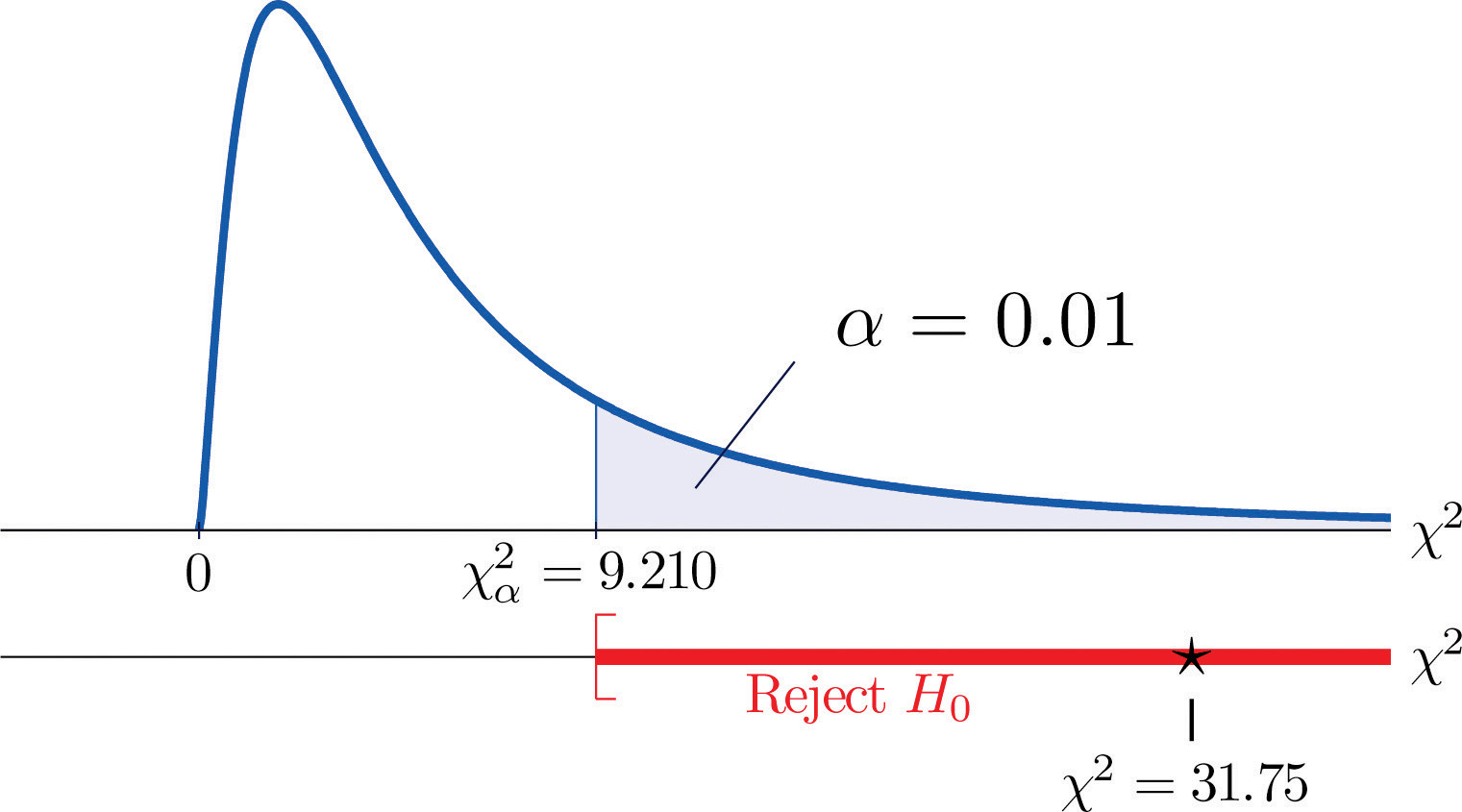
Din moment ce testul are coada dreaptă, valoarea critică este χ0,012. Citind din Figura 12.4 „Valorile critice ale distribuțiilor Chi-pătrat”, χ0.012=9.210, deci regiunea de respingere este [9.210,∞).
Pasul 5. Deoarece 31,75 > 9,21, decizia este de a respinge ipoteza nulă. A se vedea figura 11.4. Datele oferă suficiente dovezi, la un nivel de semnificație de 1%, pentru a concluziona că scorul CEE și GPA nu sunt independente: scorul de la examenul de admitere are putere de predicție.

Figura 11.4 Nota 11.9 „Exemplul 1”

Key Takeaways

Valorile critice ale unei distribuții chi-pătrat cu grade de libertate df se găsesc în figura 12.4 „Valorile critice ale distribuțiilor chi-pătrat”.
Un test chi-pătratUn test bazat pe o statistică chi-pătrat pentru a verifica dacă doi factori sunt independenți. poate fi utilizat pentru a evalua ipoteza că două variabile aleatoare sau doi factori sunt independenți.

Exerciții

Basic

Căutați χ0.012 pentru fiecare dintre următoarele numere de grade de libertate.
1. df=5
2. df=11
3. df=25
Găsește χ0,052 pentru fiecare dintre următoarele numere de grade de libertate.
1. df=6
2. df=12
3. df=30
Găsește χ0.102 pentru fiecare dintre următoarele numere de grade de libertate.
1. df=6
2. df=12
3. df=30
Găsește χ0.012 pentru fiecare dintre următoarele numere de grade de libertate.
1. df=7
2. df=10
3. df=20
Pentru df=7 și α=0.05, găsiți
1. χα2
2. χα22
Pentru df=17 și α=0.01, găsiți
1. χα2
2. χα22
Un eșantion de date este sortat într-un tabel de contingență 2 × 2 pe baza a doi factori, fiecare dintre ei având două niveluri.

.
.
.

Factorul 1

Nivelul 1 Nivelul 2 Total rând

Factorul 2 Nivelul 1 20 10 R

Nivelul 2 15 5 R

Total coloană C C n
1. Găsește totalurile coloanelor, totalurile rândurilor și totalul general, n, al tabelului.
2. Căutați numărul așteptat E de observații pentru fiecare celulă, pe baza ipotezei că cei doi factori sunt independenți (adică, folosiți doar formula E=(R×C)∕n).
3. Căutați valoarea statisticii testului chi-pătrat χ2.
4. Căutați numărul de grade de libertate al statisticii testului chi-pătrat.
Un eșantion de date este sortat într-un tabel de contingență 3 × 2 pe baza a doi factori, dintre care unul are trei niveluri și celălalt are două niveluri.

.
.
.

Factorul 1

Nivelul 1 Nivelul 2 Total rând

Factorul 2 Nivelul 1 20 10 R

Nivelul 2 15 5 R

Nivelul 3 10 20 R

Total coloană C C n
1. Găsește totalul coloanelor, totalurile rândurilor și totalul general, n, al tabelului.
2. Căutați numărul așteptat E de observații pentru fiecare celulă, pe baza ipotezei că cei doi factori sunt independenți (adică, folosiți doar formula E=(R×C)∕n).
3. Căutați valoarea statisticii testului chi-pătrat χ2.
4. Găsește numărul de grade de libertate al statisticii testului chi-pătrat.

	Factorul 1
Factorul 2	Nivelul 1	20	10	R
Nivelul 2	15	5	R
Total coloană	C	C	n

	Factorul 1
Factorul 2	Nivelul 1	20	10	R
Nivelul 2	15	5	R
Nivelul 3	10	20	R
Total coloană	C	C	n

Aplicații

Un psiholog pentru copii crede că aceștia au performanțe mai bune la teste atunci când li se oferă libertatea percepută de alegere. Pentru a testa această convingere, psihologul a realizat un experiment în care 200 de copii de clasa a treia au fost repartizați aleatoriu în două grupuri, A și B. Fiecare copil a primit același test de logică simplă. Cu toate acestea, în grupul B, fiecărui copil i s-a dat libertatea de a alege o broșură de text din mai multe cu diverse desene pe coperte. Performanța fiecărui copil a fost evaluată ca fiind foarte bună, bună și satisfăcătoare. Rezultatele sunt rezumate în tabelul furnizat. Testați, la un nivel de semnificație de 5%, dacă există suficiente dovezi în aceste date pentru a susține convingerea psihologului.

.

Grupa

A B

Performanță Mult bună 32 29

Bună 55 61

Bună 10 13

	Grupa
Performanță	Mult bună	32	29
Bună	55	61
Bună	10	13

În ceea ce privește concursurile de degustare a vinurilor, mulți experți susțin că primul pahar de vin servit stabilește un gust de referință și că un vin de referință diferit poate modifica clasamentul relativ al celorlalte vinuri din concurs. Pentru a testa această afirmație, trei vinuri, A, B și C, au fost servite la un eveniment de degustare de vinuri. Fiecărei persoane i s-a servit un singur pahar din fiecare vin, dar în ordine diferită pentru diferiți invitați. La final, fiecare persoană a fost rugată să îl numească pe cel mai bun dintre cele trei. O sută șaptezeci și două de persoane au participat la eveniment, iar cele mai bune alegeri ale acestora sunt prezentate în tabelul de mai jos. Testați, la un nivel de semnificație de 1%, dacă există suficiente dovezi în date pentru a susține afirmația că preferința experților în vinuri depinde de primul vin servit.

		Top Pick
		A	B	C
Primul pahar	A	12	31	27
	B	15	40	21
	C	10	9	7

Se lasă-stângaci este ereditară? Pentru a răspunde la această întrebare, 250 de adulți sunt selectați la întâmplare și se notează caracterul lor de stângaci și al părinților lor. Rezultatele sunt rezumate în tabelul furnizat. Testați, la un nivel de semnificație de 1%, dacă există suficiente dovezi în aceste date pentru a concluziona că există un element ereditar în ceea ce privește handicapul.

		Numărul de părinți stângaci.Stângaci
		0	1	2
Mână	Stângaci	8	10	12
Mână	Dreapta	178	21	21

Cei mai mulți geneticieni susțin că genele care determină stânga-stângăcia guvernează, de asemenea, dezvoltarea centrelor de limbaj din creier. Dacă această afirmație este adevărată, atunci ar fi rezonabil să ne așteptăm ca persoanele stângace să aibă tendința de a avea abilități lingvistice mai puternice. Un studiu conceput pentru a testa această afirmație a selectat la întâmplare 807 studenți care au susținut Graduate Record Examination (GRE). Punctajele lor la partea de limbă a examenului au fost clasificate în trei categorii: scăzut, mediu și ridicat, iar în plus a fost notată și mâna lor. Rezultatele sunt prezentate în tabelul furnizat. Testați, la un nivel de semnificație de 5%, dacă există suficiente dovezi în aceste date pentru a concluziona că stângacii tind să aibă abilități lingvistice mai puternice.

		GRE English Scores
		Low	Mediu	Superioară
Mână de lucru	Stângaci	18	40	40	22
Mână de lucru	Dreapta	201	360	166

Se crede, în general, că copiii crescuți în familii stabile au tendința de a avea rezultate bune la școală. Pentru a verifica o astfel de credință, un cercetător în științe sociale a examinat 290 de dosare ale elevilor selectați la întâmplare dintr-un liceu public și a notat structura familială și statutul academic al fiecărui elev la patru ani după ce a intrat la liceu. Datele au fost apoi sortate într-un tabel de contingență 2 × 3 cu doi factori. Factorul 1 are două niveluri: a absolvit și nu a absolvit. Factorul 2 are trei niveluri: niciun părinte, un părinte și doi părinți. Rezultatele sunt prezentate în tabelul furnizat. Testați, la un nivel de semnificație de 1%, dacă există suficiente dovezi în date pentru a concluziona că structura familiei contează în performanța școlară a elevilor.

		Statut academic
		A absolvit	Nu a absolvit
Familie	Nici un părinte	18	31
	Un părinte	101	44
	Doi părinți	70	26

Administratorul unei mari școli gimnaziale dorește să folosească influența unei celebrități pentru a încuraja elevii să facă alegeri mai sănătoase la cantina școlii. Cantina este situată în centrul unui spațiu deschis. În fiecare zi, la ora prânzului, elevii își iau prânzul și o băutură în trei rânduri separate care duc la trei stații de servire separate. Ca experiment, administratorul școlii a afișat un poster cu o vedetă pop populară din rândul adolescenților care bea lapte în fiecare dintre cele trei zone în care se oferă băuturi, cu excepția faptului că laptele din poster este diferit în fiecare locație: una arată lapte alb, una arată lapte roz cu aromă de căpșuni și una arată lapte cu ciocolată. După prima zi a experimentului, administratorul a notat alegerile de lapte ale elevilor separat pentru cele trei linii. Datele sunt prezentate în tabelul furnizat. Testați, la un nivel de semnificație de 1%, dacă există suficiente dovezi în aceste date pentru a concluziona că afișele au avut un anumit impact asupra alegerii băuturilor de către elevi.

	Student Choice
	Regular	Strawberry	Chocolate
Poster Choice
Regular	38	28	40
Strawberry	18	51	24
Chocolată	32	32	53

Large Setul de date Exercițiu

Large Setul de date 8 înregistrează rezultatul unui sondaj efectuat în rândul a 300 de adulți aleși la întâmplare care merg în mod regulat la cinematografe. Pentru fiecare persoană au fost înregistrate sexul și tipul preferat de film. Testați, la un nivel de semnificație de 5%, dacă există suficiente dovezi în date pentru a concluziona că factorii „sex” și „tipul de film preferat” sunt dependenți.

http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls

Răspunsuri

1. 152>.09,
2. 24.72,
3. 44.31
1. 10.64,
2. 18.55,
3. 40.26
1. 14.07,
2. 16.01
1. C1=35, C2=15, R1=30, R2=20, n = 50,
2. E11=21, E12=9, E21=14, E22=6,
3. χ2=0.3968,
4. df=1

χ2=0.6698, χ0.052=5.99, nu se respinge H0
χ2=72.35, χ0.012=9.21, se respinge H0
χ2=21.2784, χ0.012=9.21, se respinge H0

χ2=28.4539. df=3. Regiunea de respingere: [7.815,∞). Decizie: Se respinge H0 de independență.