Test per l’indipendenza
I test d’ipotesi incontrati in precedenza nel libro avevano a che fare con il confronto dei valori numerici di due parametri della popolazione. In questa sottosezione studieremo le ipotesi che hanno a che fare con il fatto che due variabili casuali prendano o meno i loro valori indipendentemente, o che il valore di una abbia una relazione con il valore dell’altra. Quindi le ipotesi saranno espresse in parole, non in simboli matematici. Costruiamo la discussione intorno al seguente esempio.
C’è una teoria secondo cui il sesso di un bambino nel grembo materno è legato alla frequenza cardiaca del bambino: le bambine tendono ad avere una frequenza cardiaca più alta. Supponiamo di voler testare questa teoria. Esaminiamo le registrazioni della frequenza cardiaca di 40 bambini prese durante gli ultimi controlli prenatali delle loro madri prima del parto, e a ciascuna di queste 40 registrazioni selezionate a caso calcoliamo i valori di due misure casuali: 1) il sesso e 2) la frequenza cardiaca. In questo contesto, queste due misure casuali sono spesso chiamate fattori. Poiché l’onere della prova è che la frequenza cardiaca e il genere sono correlati, non che non sono correlati, il problema di testare la teoria sul genere del bambino e la frequenza cardiaca può essere formulato come un test delle seguenti ipotesi:
H0:Il genere e la frequenza cardiaca del bambino sono indipendentivs. Ha:Il sesso del bambino e la frequenza cardiaca del bambino non sono indipendenti
Il fattore sesso ha due categorie o livelli naturali: maschio e femmina. Dividiamo il secondo fattore, la frequenza cardiaca, in due livelli, basso e alto, scegliendo una certa frequenza cardiaca, ad esempio 145 battiti al minuto, come limite tra loro. Una frequenza cardiaca inferiore a 145 battiti al minuto sarà considerata bassa e da 145 in su considerata alta. I 40 record danno origine a una tabella di contingenza 2 × 2. Unendo i totali di riga, i totali di colonna e il totale generale si ottiene la tabella mostrata come Tabella 11.1 “Sesso del bambino e frequenza cardiaca”. Le quattro voci in grassetto sono conteggi di osservazioni dal campione di n = 40. C’erano 11 ragazze con bassa frequenza cardiaca, 17 ragazzi con bassa frequenza cardiaca, e così via. Essi formano il nucleo della tabella estesa.
Tabella 11.1 Sesso del bambino e frequenza cardiaca
| Tasso cardiaco | ||||
|---|---|---|---|---|
| Basso | Alto | Totale di fila | ||
| Gender | Ragazza | 11 | 7 | 18 |
| Ragazzo | 17 | 5 | 22 | |
| Colonna Totale | 28 | 12 | Totale = 40 | |
In analogia con il fatto che la probabilità di eventi indipendenti è il prodotto delle probabilità di ciascun evento, se la frequenza cardiaca e il sesso fossero indipendenti, allora ci aspetteremmo che il numero in ogni cella centrale sia vicino al prodotto del totale della riga R e del totale della colonna C della riga e della colonna che lo contengono, diviso per la dimensione del campione n. Denotando un tale numero atteso di osservazioni E, questi quattro valori attesi sono:
- 1a riga e 1a colonna: E=(R×C)∕n=18×28∕40=12,6
- 1a riga e 2a colonna: E=(R×C)∕n=18×12∕40=5,4
- seconda riga e 1a colonna: E=(R×C)∕n=22×28∕40=15,4
- seconda riga e seconda colonna: E=(R×C)∕n=22×12∕40=6.6
Aggiorniamo la tabella 11.1 “Genere del bambino e frequenza cardiaca” mettendo ogni valore atteso nella cella centrale corrispondente, proprio sotto il valore osservato nella cella. Questo dà la tabella aggiornata 11.2 “Genere del bambino e frequenza cardiaca”.
Tabella 11.2 Genere del bambino aggiornato e frequenza cardiaca
| Tasso cardiaco | ||||
|---|---|---|---|---|
| Basso | Alto | Totale | ||
| Gender | Ragazza | O=11E=12.6 | O=7E=5.4 | R = 18 |
| Boy | O=17E=15.4 | O=5E=6.6 | R = 22 | |
| Colonna Totale | C = 28 | C = 12 | n = 40 | |
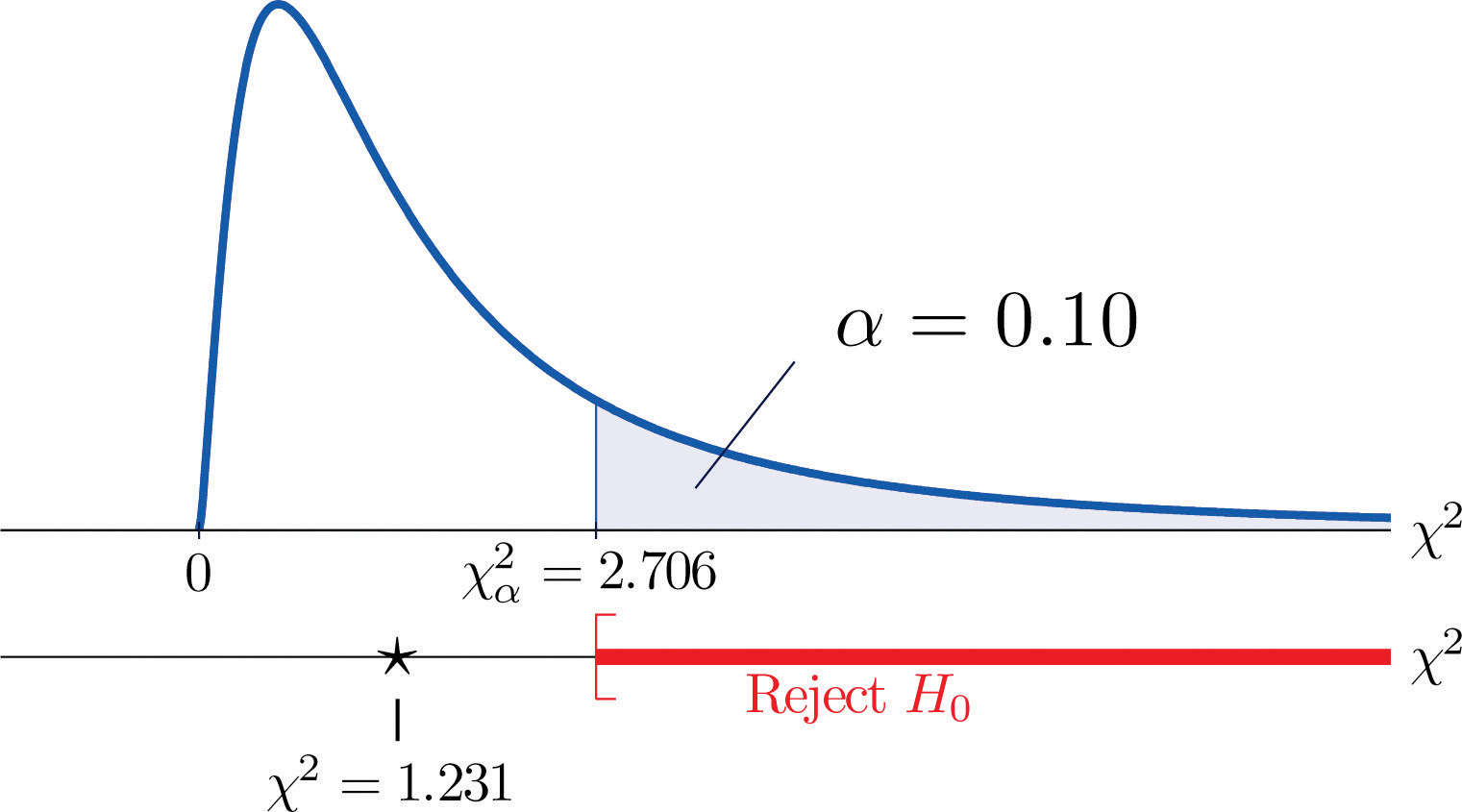
Una misura di quanto i dati deviano da quello che ci aspetteremmo di vedere se i fattori fossero davvero indipendenti è la somma dei quadrati della differenza dei numeri in ogni cella centrale, o, standardizzando dividendo ogni quadrato per il numero atteso nella cella, la somma Σ(O-E)2∕E. Rifiuteremmo l’ipotesi nulla che i fattori sono indipendenti solo se questo numero è grande, quindi il test è a coda destra. In questo esempio la variabile casuale Σ(O-E)2∕E ha la distribuzione chi-quadrato con un grado di libertà. Se avessimo deciso all’inizio di testare al livello di significatività del 10%, il valore critico che definisce la regione di rifiuto sarebbe, leggendo dalla figura 12.4 “Valori critici delle distribuzioni chi-quadro”, χα2=χ0.102=2.706, quindi la regione di rifiuto sarebbe l’intervallo [2.706,∞). Quando calcoliamo il valore della statistica standardizzata del test otteniamo
Σ(O-E)2E=(11-12.6)212.6+(7-5.4)25.4+(17-15.4)215.4+(5-6.6)26.6=1.231
Siccome 1.231 < 2.706, la decisione è di non rigettare H0. Vedi Figura 11.3 “Previsione del sesso del bambino”. I dati non forniscono prove sufficienti, al livello di significatività del 10%, per concludere che la frequenza cardiaca e il genere siano correlati.
Figura 11.3 Previsione del genere del bambino
Con questo esempio specifico in mente, passiamo ora alla situazione generale. Nell’impostazione generale di testare l’indipendenza di due fattori, chiamiamoli Fattore 1 e Fattore 2, le ipotesi da testare sono
H0:I due fattori sono indipendentivs. Ha:I due fattori non sono indipendenti
Come nell’esempio ogni fattore è diviso in un certo numero di categorie o livelli. Questi potrebbero sorgere naturalmente, come nella divisione ragazzo-ragazza del sesso, o in qualche modo arbitrariamente, come nella divisione alto-basso della frequenza cardiaca. Supponiamo che il Fattore 1 abbia livelli I e il Fattore 2 abbia livelli J. Allora le informazioni di un campione casuale danno luogo a una tabella di contingenza generale I × J, che con i totali di riga, i totali di colonna e un totale generale apparirebbe come mostrato nella Tabella 11.3 “Tabella di contingenza generale”. Ogni cella può essere etichettata da una coppia di indici (i,j). Oij sta per il conteggio osservato delle osservazioni nella cella nella riga i e nella colonna j, Ri per il totale della riga i e Cj per il totale della colonna j. Per semplificare la notazione elimineremo gli indici, così la Tabella 11.3 “Tabella di contingenza generale” diventa la Tabella 11.4 “Tabella di contingenza generale semplificata”. Tuttavia è importante tenere a mente che gli Os, gli R e i C, anche se denotati dagli stessi simboli, sono in realtà numeri diversi.
Tabella 11.3 Tabella di contingenza generale
| Livelli del fattore 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – | J | Totale fila | ||
| Livelli del fattore 1 | 1 | O11 | – – | O1j | – – – | O1J | R1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| i | Oi1 | – – – | Oij | – – – | OiJ | Ri | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| I | OI1 | – – – | OIj | – – | OIJ | RI | |
| Totale colonna | C1 | – – – | Cj | – – | CJ | n | |
Tabella 11.4 Tabella di contingenza generale semplificata
| Livelli fattore 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – | J | Totale delle righe | ||||
| Livelli fattore 1 | 1 | O | – – – | O | – – | O | R | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| i | O | – – – | O | – – – | O | R | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||||
| I | O | – – – | O | – – | O | R | |||
| Totale colonna | C | – – – | C | – – | C | n | |||
Come nell’esempio, per ogni cella centrale della tabella calcoliamo quale sarebbe il numero atteso E di osservazioni se i due fattori fossero indipendenti. E è calcolato per ogni cella centrale (ogni cella con una O) della tabella 11.4 “Tabella di contingenza generale semplificata” con la regola applicata nell’esempio:
dove R è il totale della riga e C è il totale della colonna corrispondente alla cella, e n è la dimensione del campione.
Dopo aver calcolato il numero atteso per ogni cella, la Tabella 11.4 “Tabella di contingenza generale semplificata” viene aggiornata per formare la Tabella 11.5 “Tabella di contingenza generale aggiornata” inserendo il valore calcolato di E in ogni cella centrale.
Tabella 11.5 Tabella di contingenza generale aggiornata
| Livelli fattore 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | – – – | j | – – | J | Totale fila | |||||
| Livelli fattore 1 | 1 | OE | – – | OE | – – – | OE | R | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||||
| i | OE | – – – | OE | – – – | OE | R | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||||
| I | OE | – – | OE | – – – | OE | R | ||||
| Totale colonna | C | – – | C | – – | C | – – | C | n | ||
Ecco la statistica di test per l’ipotesi generale basata sulla tabella 11.5 “Tabella di contingenza generale aggiornata”, insieme alle condizioni che segua una distribuzione chi-quadro.
Statistica di test per testare l’indipendenza di due fattori
χ2=Σ(O-E)2E
dove la somma è su tutte le celle centrali della tabella.
Se
- i due fattori di studio sono indipendenti, e
- il conteggio osservato O di ogni cella nella Tabella 11.5 “Tabella di contingenza generale aggiornata” è almeno 5,
allora χ2 segue approssimativamente una distribuzione chi-quadro con df=(I-1)×(J-1) gradi di libertà.
Per eseguire il test, che è sempre a coda destra, si utilizzano le stesse procedure in cinque fasi, sia l’approccio del valore critico che quello del valore p, che sono state introdotte nella Sezione 8.1 “Gli elementi della verifica delle ipotesi” e nella Sezione 8.3 “La significatività osservata di un test” del Capitolo 8 “Verifica delle ipotesi”.
Esempio 1
Un ricercatore desidera indagare se i punteggi degli studenti in un esame di ammissione al college (CEE) hanno un qualche potere indicativo per il futuro rendimento al college misurato dal GPA. In altre parole, vuole indagare se i fattori CEE e GPA sono indipendenti o meno. Seleziona a caso n = 100 studenti in un college e annota il punteggio di ogni studente all’esame di ammissione e la sua media dei voti alla fine del secondo anno. Divide i punteggi dell’esame di ammissione in due livelli e le medie dei voti in tre livelli. Ordinando i dati secondo queste divisioni, forma la tabella di contingenza mostrata come Tabella 11.6 “CEE versus GPA Contingency Table”, in cui i totali di riga e colonna sono già stati calcolati.
Tabella 11.6 CEE contro GPA Tabella di contingenza
| GPA | |||||
|---|---|---|---|---|---|
| <2.7 | 2.7 a 3.2 | >3.2 | Riga Totale | ||
| CEE | 1800 | 35 | 12 | 5 | 52 |
| ≥1800 | 6 | 24 | 18 | 48 | |
| Colonna Totale | 41 | 36 | 23 | Totale=100 | |
Test, al livello di significatività dell’1%, se questi dati forniscono prove sufficienti per concludere che i punteggi CEE indicano i futuri livelli di rendimento delle matricole universitarie in arrivo, misurati dal GPA.
Soluzione:
Eseguiamo il test utilizzando l’approccio del valore critico, seguendo il consueto metodo in cinque fasi delineato alla fine della Sezione 8.1 “Gli elementi della verifica delle ipotesi” nel Capitolo 8 “Verifica delle ipotesi”.
-
Step 1. Le ipotesi sono
H0:CEE e GPA sono fattori indipendentivs. Ha:CEE e GPA non sono fattori indipendenti
- Passo 2. La distribuzione è chi-quadrato.
-
Passo 3. Per calcolare il valore della statistica del test dobbiamo prima calcolare il numero atteso per ciascuna delle sei celle centrali (quelle le cui voci sono in grassetto):
- 1a riga e 1a colonna: E=(R×C)∕n=41×52∕100=21,32
- 1a riga e 2a colonna: E=(R×C)∕n=36×52∕100=18,72
- 1a riga e 3a colonna: E=(R×C)∕n=23×52∕100=11,96
- Seconda riga e 1a colonna: E=(R×C)∕n=41×48∕100=19,68
- Seconda riga e 2a colonna: E=(R×C)∕n=36×48∕100=17,28
- seconda riga e terza colonna: E=(R×C)∕n=23×48∕100=11.04
Tabella 11.6 “CEE versus GPA Contingency Table” è aggiornata alla tabella 11.7 “Updated CEE versus GPA Contingency Table”.
Tabella 11.7 Tabella di contingenza CEE contro GPA aggiornata
GPA <2.7 2.7 a 3.2 >3.2 Row Total CEE 1800 O=35E=21.32 O=12E=18.72 O=5E=11.96 R = 52 ≥1800 O=6E=19.68 O=24E=17.28 O=18E=11.04 R = 48 Colonna Totale C = 41 C = 36 C = 23 n = 100 La statistica del test è
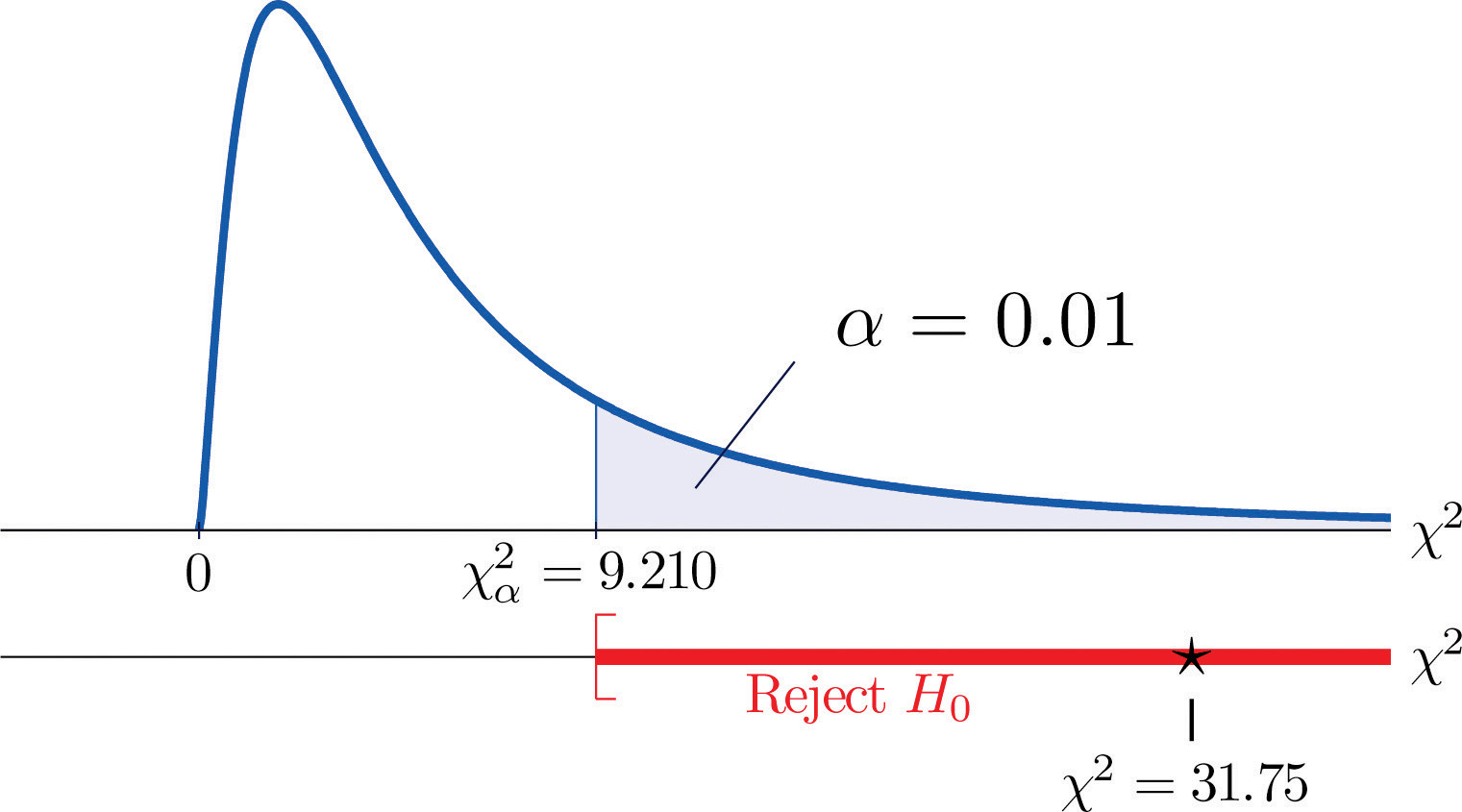
χ2=Σ(O-E)2E=(35-21.32)221.32+(12−18.72)218.72+(5−11.96)211.96+(6−19.68)219.68+(24−17.28)217.28+(18−11.04)211.04=31.75
-
Step 4. Poiché il fattore CEE ha due livelli e il fattore GPA ne ha tre, I = 2 e J = 3. Quindi la statistica del test segue la distribuzione chi-quadro con df=(2-1)×(3-1)=2 gradi di libertà.
Siccome il test è a coda destra, il valore critico è χ0,012. Leggendo dalla Figura 12.4 “Valori critici delle distribuzioni Chi-quadro”, χ0.012=9.210, quindi la regione di rifiuto è [9.210,∞).
- Passo 5. Poiché 31,75 > 9,21 la decisione è di rifiutare l’ipotesi nulla. Vedi Figura 11.4. I dati forniscono prove sufficienti, al livello di significatività dell’1%, per concludere che il punteggio CEE e il GPA non sono indipendenti: il punteggio dell’esame di ammissione ha potere predittivo.
Figura 11.4 Nota 11.9 “Esempio 1”
Key Takeaways
- I valori critici di una distribuzione chi-quadro con gradi di libertà df si trovano nella Figura 12.4 “Valori critici delle distribuzioni chi-quadro”.
- Un test chi-quadratoUn test basato su una statistica chi-quadro per controllare se due fattori sono indipendenti. può essere usato per valutare l’ipotesi che due variabili casuali o fattori siano indipendenti.
Esercizi
-
Trova χ0,012 per ciascuno dei seguenti gradi di libertà.
- df=5
- df=11
- df=25
-
Trova χ0,052 per ognuno dei seguenti gradi di libertà.
- df=6
- df=12
- df=30
-
Trova χ0.102 per ciascuno del seguente numero di gradi di libertà.
- df=6
- df=12
- df=30
-
Trova χ0.012 per ciascuno del seguente numero di gradi di libertà.
- df=7
- df=10
- df=20
-
Per df=7 e α=0.05, trovare
- χα2
- χα22
-
Per df=17 e α=0.01, trovare
- χα2
- χα22
-
Un campione di dati è ordinato in una tabella di contingenza 2 × 2 basata su due fattori, ognuno dei quali ha due livelli.
Fattore 1 Livello 1 Livello 2 Riga Totale Fattore 2 Livello 1 20 10 R Livello 2 15 5 R Totale colonna C C N - Trova i totali di colonna, i totali di riga e il totale generale, n, della tabella.
- Trova il numero atteso E di osservazioni per ogni cella in base all’ipotesi che i due fattori siano indipendenti (cioè, basta usare la formula E=(R×C)∕n).
- Trova il valore del test statistico chi-quadrato χ2.
- Trova il numero di gradi di libertà della statistica del test del chi-quadrato.
-
Un campione di dati è ordinato in una tabella di contingenza 3 × 2 basata su due fattori, uno dei quali ha tre livelli e l’altro ha due livelli.
Fattore 1 Livello 1 Livello 2 Riga Totale Fattore 2 Livello 1 20 10 R Livello 2 15 5 R Livello 3 10 20 R Totale di colonna C C n - Cerca i totali di colonna, i totali di riga e il totale generale, n, della tabella.
- Trova il numero atteso E di osservazioni per ogni cella in base all’ipotesi che i due fattori siano indipendenti (cioè, basta usare la formula E=(R×C)∕n).
- Trova il valore del test statistico chi-quadrato χ2.
- Trova il numero di gradi di libertà della statistica del test del chi-quadrato.
Basico
-
Uno psicologo infantile crede che i bambini eseguano meglio i test quando viene data loro la libertà di scelta percepita. Per testare questa convinzione, lo psicologo ha condotto un esperimento in cui 200 bambini di terza elementare sono stati assegnati a caso a due gruppi, A e B. Ogni bambino ha ricevuto lo stesso semplice test di logica. Tuttavia, nel gruppo B, ad ogni bambino è stata data la libertà di scegliere un libretto di testo tra molti con vari disegni sulle copertine. La prestazione di ogni bambino è stata valutata come Molto buona, Buona e Discreta. I risultati sono riassunti nella tabella fornita. Testate, al livello di significatività del 5%, se ci sono prove sufficienti nei dati per sostenere la convinzione dello psicologo.
Gruppo A B Performance Molto Buono 32 29 Buono 55 61 Buono 10 13 -
Per quanto riguarda le gare di degustazione di vini, molti esperti sostengono che il primo bicchiere di vino servito stabilisce un gusto di riferimento e che un vino di riferimento diverso può alterare la classifica relativa degli altri vini in concorso. Per testare questa affermazione, tre vini, A, B e C, sono stati serviti in una degustazione di vini. Ad ogni persona è stato servito un singolo bicchiere di ogni vino, ma in ordini diversi per i diversi ospiti. Alla fine, ad ogni persona è stato chiesto di nominare il migliore dei tre. Centosettantadue persone erano presenti all’evento e le loro scelte migliori sono riportate nella tabella fornita. Testare, al livello di significatività dell’1%, se ci sono prove sufficienti nei dati per sostenere l’affermazione che la preferenza degli esperti di vino dipende dal primo vino servito.
Top Pick A B C Primo Vetro A 12 31 27 B 15 40 21 C 10 9 7 -
Essere mancinimancino è ereditario? Per rispondere a questa domanda, 250 adulti sono stati selezionati a caso e sono stati annotati il loro senso della mano e quello dei loro genitori. I risultati sono riassunti nella tabella fornita. Verifica, al livello di significatività dell’1%, se ci sono prove sufficienti nei dati per concludere che c’è un elemento ereditario nella manualità.
Numero di genitori manciniMano sinistra 0 1 2 Mano Sinistra 8 10 12 Destra 178 21 21 -
Alcuni genetisti sostengono che i geni che determinano la sinistramancini governano anche lo sviluppo dei centri del linguaggio del cervello. Se questa affermazione è vera, allora sarebbe ragionevole aspettarsi che i mancini tendano ad avere capacità linguistiche più forti. Uno studio progettato per testare questa affermazione ha selezionato a caso 807 studenti che hanno preso il Graduate Record Examination (GRE). I loro punteggi nella parte linguistica dell’esame sono stati classificati in tre categorie: basso, medio e alto, e il loro mancinismo è stato anche annotato. I risultati sono riportati nella tabella fornita. Testate, al livello di significatività del 5%, se ci sono prove sufficienti nei dati per concludere che i mancini tendono ad avere capacità linguistiche più forti.
Punteggi GRE inglese Basso Media Alto Manovra Sinistra 18 40 22 Destra 201 360 166 -
Si crede generalmente che i bambini cresciuti in famiglie stabili tendano ad andare bene a scuola. Per verificare tale credenza, uno scienziato sociale ha esaminato 290 registri di studenti selezionati a caso in una scuola superiore pubblica e ha annotato la struttura familiare e lo stato accademico di ogni studente quattro anni dopo essere entrato nella scuola superiore. I dati sono stati poi ordinati in una tabella di contingenza 2 × 3 con due fattori. Il fattore 1 ha due livelli: laureato e non laureato. Il fattore 2 ha tre livelli: nessun genitore, un genitore e due genitori. I risultati sono riportati nella tabella fornita. Testate, al livello di significatività dell’1%, se ci sono prove sufficienti nei dati per concludere che la struttura familiare conta nel rendimento scolastico degli studenti.
Stato accademico Laureato Non laureato Famiglia Nessun genitore 18 31 Un genitore 101 44 Due genitori 70 26 -
L’amministratore di una grande scuola media vuole usare l’influenza della celebrità per incoraggiare gli studenti a fare scelte più sane nella mensa scolastica. La mensa è situata al centro di uno spazio aperto. Ogni giorno all’ora di pranzo gli studenti prendono il loro pranzo e una bevanda in tre file separate che portano a tre stazioni di servizio separate. Come esperimento, l’amministratore della scuola ha esposto un poster di una popolare pop star adolescente che beve latte in ciascuna delle tre aree in cui vengono fornite le bevande, tranne che il latte nel poster è diverso in ogni posizione: una mostra il latte bianco, una mostra il latte rosa al gusto di fragola e una mostra il latte al cioccolato. Dopo il primo giorno dell’esperimento, l’amministratore ha annotato le scelte di latte degli studenti separatamente per le tre linee. I dati sono riportati nella tabella fornita. Testate, al livello di significatività dell’1%, se ci sono prove sufficienti nei dati per concludere che i poster hanno avuto un certo impatto sulle scelte delle bevande degli studenti.
Student Choice Regular Strawberry Chocolate Poster Choice Regolare 38 28 40 Strawberry 18 51 24 Cioccolato 32 32 53
Applicazioni
-
Grande Il set di dati 8 registra il risultato di un sondaggio su 300 adulti selezionati a caso che vanno regolarmente al cinema. Per ogni persona sono stati registrati il sesso e il tipo di film preferito. Testate, al livello di significatività del 5%, se nei dati ci sono prove sufficienti per concludere che i fattori “genere” e “tipo di film preferito” sono dipendenti.
http://www.gone.2012books.lardbucket.org/sites/all/files/data8.xls
Grande Set di dati Esercizio
Risposte
-
- 15.09,
- 24.72,
- 44.31
-
- 10.64,
- 18.55,
- 40.26
-
- 14.07,
- 16.01
-
- C1=35, C2=15, R1=30, R2=20, n = 50,
- E11=21, E12=9, E21=14, E22=6,
- χ2=0.3968,
- df=1
-
χ2=0,6698, χ0.052=5.99, non rifiutare H0
-
χ2=72.35, χ0.012=9.21, rifiutare H0
-
χ2=21.2784, χ0.012=9.21, rifiutare H0
-
χ2=28.4539. df=3. Regione di rifiuto: [7.815,∞). Decisione: Rifiutare H0 di indipendenza.